
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Прямой ход метода Гаусса
|
|
Шаг 1. Если а 11 = 0, то с помощью преобразования 1 добиваемся, чтобы на место этого элемента попал ненулевой элемент (при применении этого преобразования к столбцам матрицы исключением является последний столбец, он должен оставаться неподвижным). Если в матрице нет ненулевых элементов, то она имеет трапециевидную форму, и прямой ход завершен. Пусть 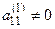 (верхний индекс указывает на номер шага), умножим элемент первой строки на число
(верхний индекс указывает на номер шага), умножим элемент первой строки на число 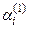 и прибавим к соответствующим элементам i -й строки i = 2, 3,...., m. Числа
и прибавим к соответствующим элементам i -й строки i = 2, 3,...., m. Числа 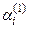 подберем так, чтобы первые элементы в строках обратились в 0, т.е.
подберем так, чтобы первые элементы в строках обратились в 0, т.е. 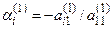 . В результате получим матрицу, в которой в первом столбце под главной диагональю все элементы равны 0. Обозначим
. В результате получим матрицу, в которой в первом столбце под главной диагональю все элементы равны 0. Обозначим
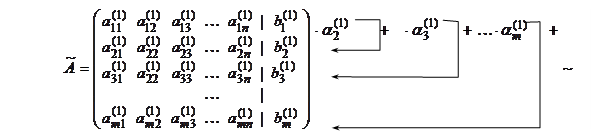 |
полученную матрицу
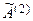 :
:
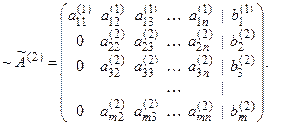
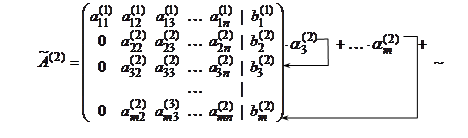 |
Шаг 2. Если
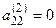 , то с помощью преобразования 1 добиваемся, чтобы на место этого элемента попал ненулевой элемент матрицы. Если в этой матрице нет ненулевых элементов, то она имеет трапециевидную форму, и прямой ход завершен. Пусть
, то с помощью преобразования 1 добиваемся, чтобы на место этого элемента попал ненулевой элемент матрицы. Если в этой матрице нет ненулевых элементов, то она имеет трапециевидную форму, и прямой ход завершен. Пусть  , умножим элементы второй строки на число
, умножим элементы второй строки на число 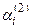 и прибавим к соответствующим элементам i -й строки i = 3, 4,..., m. Числа
и прибавим к соответствующим элементам i -й строки i = 3, 4,..., m. Числа 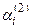 подберем так, чтобы вторые элементы в строках обратились в нули, т.е.
подберем так, чтобы вторые элементы в строках обратились в нули, т.е. 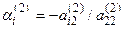 :
:
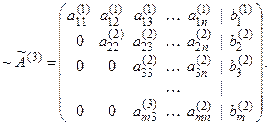
В результате, получим матрицу, в которой во втором столбце под главной диагональю все элементы равны нулю.
Будем выполнять указанные преобразования до тех пор, пока матрица системы А не примет трапециевидную форму, пусть это произойдет на шаге r, т.е.
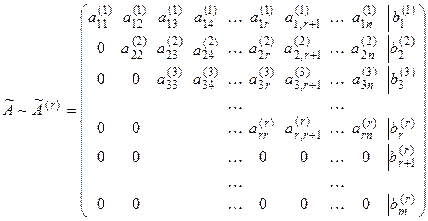 .
.
Этой матрице соответствует система уравнений, эквивалентная исходной (1.11), вида:
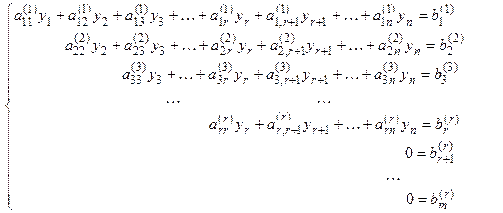 . (1.14)
. (1.14)
Здесь неизвестные обозначены: y 1, …, yn, потому что при применении элементарного преобразования 1 к столбцам расширенной матрицы естественный порядок переменных х 1, х 2 …, хn нарушается. Например, если в расширенной матрице поменяли местами столбцы с номерами k и р, то в системе на месте слагаемых с номерами неизвестных k будут слагаемые с номерами неизвестных р и наоборот, т.е. уk = xp и уp = хk. На этом прямой ход метода Гаусса заканчивается.
|
|