
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теорема 1.2 (Кронекера-Капелли)
|
|
Для того чтобы система (1.11) была совместной, необходимо и достаточно, чтобы rang A = rang 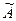 .
.
Доказательство. При помощи прямого хода метода Гаусса, приведем систему (1.11) к виду (1.14).
Необходимость. Если система (1.11), совместна, то и система (1.14) тоже совместна, тогда

(если это не так, например, 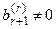 , то (r + 1)-е уравнение
, то (r + 1)-е уравнение 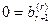 не имеет решений, т.е. система несовместна, что противоречит условию). Откуда следует, что в трапециевидных матрицах, эквивалентных матрице системы и расширенной матрице (первая получается из второй удалением последнего столбца), содержится одинаковое число ненулевых строк, значит rang A = rang
не имеет решений, т.е. система несовместна, что противоречит условию). Откуда следует, что в трапециевидных матрицах, эквивалентных матрице системы и расширенной матрице (первая получается из второй удалением последнего столбца), содержится одинаковое число ненулевых строк, значит rang A = rang 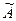 .
.
Достаточность. Если rang A = rang 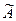 , то
, то  (если это не так, например
(если это не так, например 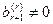 , то у матрицы, эквивалентной матрице
, то у матрицы, эквивалентной матрице 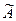 , будет хотя бы на одну ненулевую строку больше, чем в матрице, эквивалентной матрице А, т.е. rang A < rang
, будет хотя бы на одну ненулевую строку больше, чем в матрице, эквивалентной матрице А, т.е. rang A < rang 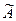 , что противоречит условию). Отбросим последние m – r уравнений в системе (1.14), получим систему r уравнений, которая будет эквивалентна системе (1.14), а значит и системе (1.11) (так как последние уравнения превращаются в тождества 0 = 0).
, что противоречит условию). Отбросим последние m – r уравнений в системе (1.14), получим систему r уравнений, которая будет эквивалентна системе (1.14), а значит и системе (1.11) (так как последние уравнения превращаются в тождества 0 = 0).
Назовем неизвестные у 1, y 2,..., уr базисными, а уr +1, уr +2, …, уn свободными и перенесем слагаемые, содержащие свободные неизвестные, в правую часть уравнений. Получим систему относительно базисных неизвестных:
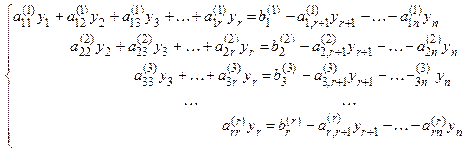 , (1.15)
, (1.15)
которая эквивалентна (1.11), и для каждого набора значений свободных неизвестных yr +1 = t 1, yr +2 = t 2, …, yn = tn–r по теореме 1.1 имеет единственное решение.
|
|