Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Columns 1 through 6

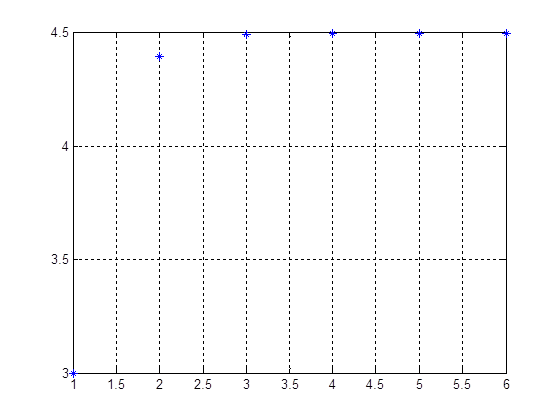
3.0000 4.3906 4.4885 4.4932 4.4934 4.4934

Column 7

4.4934

b = 4.4934

2)

[a b]=resh('(2*x+1)^(1/5)', 0.2, 1.5, 0.0001)

a =

Columns 1 through 4

1.500000000000000 1.319507910772894 1.294782404057857 1.291244128577547

Column 5

1.290734608928400

b = 1.290734608928400

> > solve('x^5-2*x-1=0')

ans =

-1

1.2906488013467096223921797549956

-0.51879006367588422190745389443528

0.11407063116458729975763706971986 - 1.2167460039743506291763945520664*i

1.2167460039743506291763945520664*i + 0.11407063116458729975763706971986

Сравнив ответы, видим что при решении таким способом, из-за преобразований необходимых для приведения к виду мы можем потерять корни.

Упражнение 5

Создать M-функцию, которая для произвольной матрицы проверяет условия сжатости.

Если ни одно из условий сжатости для матричного уравнения не выполняется, то следует разделить каждое уравнение системы на максимальный по модулю коэффициент и получить равносильную систему.

function [m]=czhmat(c)

n=max(size(c));

r3=0;

k=0;

for j=1: n

ro1(j)=0;

ro2(j)=0;

for i=1: n

ro1(j)=ro1(j)+abs(c(j, i));

ro2(j)=ro2(j)+abs(c(i, j));

r3=r3+(c(i, j))^2;

end

end

r1=max(ro1);

r2=max(ro2);

r3=sqrt(r3);

if ((r1< 1)||(r2< 1)||(r3< 1))

m=c;

else

m=c./max(r1, max(r2, r3));

end

> > x=[1 4 3; 3 2 54; 1 42 3]

x =

1 4 3

3 2 54

1 42 3

> > a=czhmat(x)

a =

0.014541705431976 0.058166821727906 0.043625116295929

0.043625116295929 0.029083410863953 0.785252093326730

0.014541705431976 0.610751628143012 0.043625116295929

> > czhmat(a)

ans =

0.014541705431976 0.058166821727906 0.043625116295929

0.043625116295929 0.029083410863953 0.785252093326730

0.014541705431976 0.610751628143012 0.043625116295929

Упражнение 6