Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Го порядка

Модуляторы 1-го порядка, соединяемые каскадно, имеют еще один дополнительный выход, на котором формируется разность Q (U _n) – U _n = 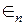, которая характеризует ошибку квантования данного каскада (рис. 5.9).

Схема двухкаскадного сигма-дельта модулятора, состоящая из двух модуляторов 1-го порядка, показана на рис. 5.10. Сигнал ошибки 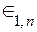первого каскада подается на вход второго каскада модулятора, где с ним производятся те же операции, что и с входным аналоговым сигналом в первом каскаде.

Выходные двухуровневые сигналы обоих каскадов подаются на линейную комбинаторную схему, которая производит с ними операции, определяемые ее структурой. Результатом этих операций (сложение, вычитание, задержка на один такт) будет появление на выходе модулятора уже не двухуровневого, а четырехуровневого сигнала с возможными значениями –3, –1, +1, +3 (если уровни выходных сигналов каждого из каскадов принять за –1 и +1).

В отличие от модулятора 2-го порядка, двухкаскадная схема вполне устойчива, и поведение ее так же предсказуемо, как и поведение одноконтурного модулятора 1-го порядка. Тем не менее, точность преобразования здесь гораздо выше.

Средняя величина шума квантования для многокаскадного сигма-дельта модулятора уменьшается пропорционально величине I / K ^2m+1, где K – коэффициент передискретизации, а m – число каскадов модулятора. Фактически, величина шума на выходе многокаскадного сигма-дельта модулятора равна уровню шумов последнего каскада.

Таким образом, очевидно, что для получения нужного значения величины шума в полосе частот преобразуемого сигнала, т.е. для повышения точности преобразования, нет необходимости использовать чрезмерно высокую тактовую частоту, а достаточно увеличить число каскадов в схеме модулятора. Техника многокаскадного понижения шума в системах А/Ц- и Ц/А-преобразования широко применяется в изделиях фирмы Matsushita и известна как система MASH (Multi Stage Noise Shaping).

На рис. 5.11 представлена обобщенная структурная схема m-каскадного сигма-дельта преобразователя. Символами «Σ Δ» на ней обозначены одноконтурные Σ Δ -модуляторы 1-го порядка, каждый из которых имеет архитектуру, показанную на рис. 5.9. Аналоговый входной сигнал Xn поступает на вход модулятора первого каскада Σ Δ ₁. Ошибка квантования 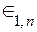этого каскада поступает на вход модулятора второго каскада Σ Δ ₂ и так далее, до m-го каскада.

Ошибка квантования последнего m -го каскада не используется. Выходы Q (U_{i , n}) всех каскадов поступают на линейную комбинаторную схему, где над ними производится еще ряд операций, которые описываются разностными уравнениями:

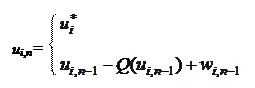при n = 0

(5.5)

при n = 1, 2, …, i = 1, 2, … m

при n = 0, 1, i = 1, 2, … m (5.6)

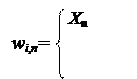при i = 1

(5.7)

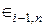при i = 2, 3, … m, n = 0, 1, …

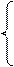+ B при u ≥ 0

где Q (u) =

– B при u < 0

u_{i , n} – выходной сигнал интегратора i -го каскада;

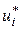- исходное состояние интегратора i -го каскада;

w_{i , n} – входной сигнал i -го каскада;

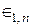– ошибка квантования i -го каскада;

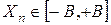– входной сигнал Σ Δ -модулятора, изменяющийся в пределах от – В до + В.

Из (5.5) и (5.6) получим:

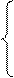
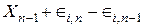для i = 1

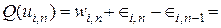(5.8)

для i = 2, 3, … m

Оператор обратной разности l означает, что для некоторого сигнала λ (в данной схеме λ соответствует Q (u_{i , n}))

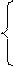λ _n для i = 0

lⁱ λ _n =

l^{i- 1}λ _n – l^{i- 1}λ _{n- 1} для i = 1, 2, …, m

Например,

l ¹λ _n = λ _n – λ _n-1, а

l ²λ _n = (λ _n – λ _n-1) – (λ _{n- 1} – λ _{n- 2}) = λ _n – 2λ _n-1 + λ _{n- 2}.

Следует отметить, что Z-образом оператора l является передаточная функция (1 – Z^-1) ⁱ.

Работа линейной комбинаторной схемы описывается уравнением:

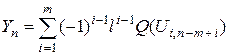, при m = 2, 3, … (5.9)

где Y_n – выходной сигнал линейной комбинаторной схемы.

Очевидно, что это уравнение полностью отражает архитектуру данной схемы. Доказано, что для m -каскадного Σ Δ -модулятора с линейной комбинаторной схемой, описываемой уравнением (5.9), выходной сигнал Y_n может быть представлен в виде суммы задержанного на m тактов входного сигнала Х_n и обратной разности m -го порядка (l ^m) ошибки двухуровневого квантования на последнем m -м этапе (в m -м каскаде):

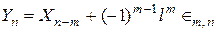(5.10)

Уравнения (5.9) и (5.10) описывают один и тот же сигнал Y_n. При этом выражение (5.9) определяет реализацию схемы Σ Δ -модулятора, а (5.10) необходимо для анализа шумов квантования на ее выходе, уровень которых можно определить как

N_n = Y_n – X_n-m.

Из уравнения (5.10) и определения оператора l следует, что N_n можно интерпретировать как результат прохождения шума двухуровневого квантователя последнего m -го каскада модулятора через усредняющий фильтр с передаточной характеристикой (–1) ^{m -1} (1–Z^-1) ^m.

Спектр мощности полного шума квантования на выходе m -каскадного Σ Δ -модулятора выражается как

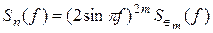(5.11)

где - спектр мощности шума квантования на выходе последнего m -го каскада.

Пример построения 3-каскадного Σ Δ -модулятора в соответствии с уравнением (5.9) показан на рис. 5.12.