
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Повне дослідження функції.
|
|
План
1. Інтервали монотонності
2. Проміжки опуклості
3. Асимптоти
4. Найбільше та найменше значення функції
5. Побудова графіків
Похідна функції має широке застосування при розв’язуванні різних задач математики, фізики, техніки та економіки. Так, наприклад, за допомогою похідної можна обчислити границю функції, знайти екстремум функції, інтервали монотонності, точки перегину функції та інше.
Інтервалами монотонності функції називаються ті інтервали, на яких функція або тільки зростає, або тільки спадає або залишається сталою.
Якщо неперервна на сегменті 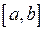 функція
функція 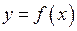 має в кожній точці цього сегмента додатну похідну, то вона зростає на цьому сегменті, а якщо від’ємну похідну, то вона спадає на цьому сегменті.
має в кожній точці цього сегмента додатну похідну, то вона зростає на цьому сегменті, а якщо від’ємну похідну, то вона спадає на цьому сегменті.
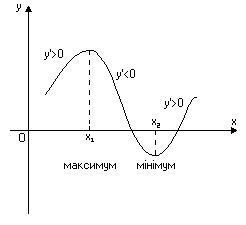 Функція
Функція 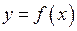 має максимум в точці
має максимум в точці 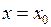 , якщо для довільних точок із її околу виконується умова
, якщо для довільних точок із її околу виконується умова  і має мінімум в точці, якщо виконується така умова:
і має мінімум в точці, якщо виконується така умова: 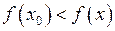 .
.
Максимум і мінімум функції називають екстремуми функції.
Необхідною умовою існування екстремуму в точці 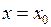 диференційовної функції
диференційовної функції 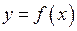 є рівність нулю її похідної:
є рівність нулю її похідної: 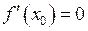 .
.
Критичними або стаціонарними точками неперервної функції 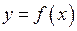 є ті точки, в яких її похідна дорівнює нулю або не існує.
є ті точки, в яких її похідна дорівнює нулю або не існує.
|
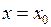 для диференційовної функції
для диференційовної функції 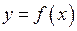 є зміна знака похідної при переході через цю точку. Так при зміні знака з “+” на “–” в точці
є зміна знака похідної при переході через цю точку. Так при зміні знака з “+” на “–” в точці 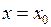 функція має максимум, а з “–” на “+” – мінімум (Рис. 6).
функція має максимум, а з “–” на “+” – мінімум (Рис. 6).
 Вгнутим називається графік диференційовної функції
Вгнутим називається графік диференційовної функції 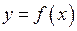 в інтервалі
в інтервалі 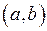 , якщо він знаходиться вище довільної його дотичної на цьому інтервалі.
, якщо він знаходиться вище довільної його дотичної на цьому інтервалі.
|
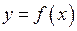 в інтервалі
в інтервалі 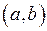 , якщо він знаходиться нижче довільної його дотичної на цьому інтервалі.
, якщо він знаходиться нижче довільної його дотичної на цьому інтервалі.
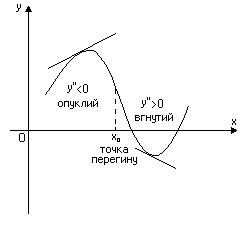
Точкою перегину неперервної функції називається та точка, яка відділяє вгнутість від опуклості її графіка (Рис. 7).
Якщо друга похідна функції 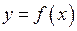 для всіх
для всіх 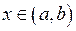 від’ємна (
від’ємна (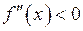 ), то тут графік функції опуклий, а якщо
), то тут графік функції опуклий, а якщо 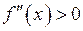 – вгнутий.
– вгнутий.
Необхідною умовою існування точки перегину графіка функції є рівність нулю її другої похідної: 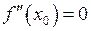 в даній точці
в даній точці 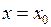 .
.
Точка 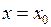 , в якій
, в якій 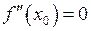 , називається критичною точкою другого порядку для функції
, називається критичною точкою другого порядку для функції 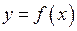 .
.
Достатньою умовою існування точки перегину графіка неперервної функції є зміна знаку другої похідної при переході через точку  .
.
Асимптотою графіка функції 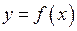 називається пряма лінія, до якої графік функції наближається на нескінченності.
називається пряма лінія, до якої графік функції наближається на нескінченності.
Вертикальною асимптотою є пряма  , якщо виконується умова
, якщо виконується умова 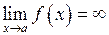 .
.
Для функції 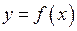 вертикальні асимптоти існують в її точках розриву другого роду.
вертикальні асимптоти існують в її точках розриву другого роду.
Похилу асимптоту шукають у вигляді  , а параметри
, а параметри 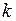 і
і 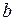 шукають за формулами:
шукають за формулами:
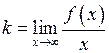 ,
,  . (23)
. (23)
Якщо хоча б одна границя не існує, то похила асимптота відсутня.
При знаходженні границь (23) інколи зручно використовувати правило Лопіталя: якщо границя відношення двох функцій 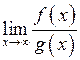 є невизначеністю виду
є невизначеністю виду 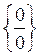 або
або 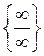 , то її можна знаходити за формулою
, то її можна знаходити за формулою
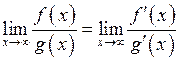 ,
,
якщо остання границя існує.
Приклад 18. Знайти найбільше та найменше значення функції 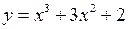 на відрізку
на відрізку 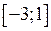 .
.
Розв’язання. Функція може досягати свого найбільшого та найменшого значення або на кінцях відрізка, або у критичних точках, якщо вони знаходяться у середині відрізка. Знайдемо критичні точки функції і розглянемо тільки ті, які потрапляють в інтервал 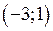 .
.

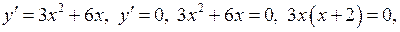
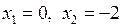 .
.
Обчислимо значення функції у критичних точках та на кінцях відрізка. Одержимо:
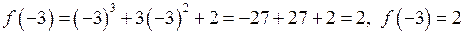 ;
;
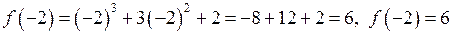 ;
;
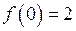 ;
; 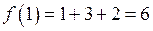 .
.
Відповідь: 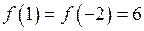 – найбільше значення функції;
– найбільше значення функції; 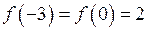 – найменше значення функції на відрізку.
– найменше значення функції на відрізку.
Приклад 19. Провести повне дослідження функції  та побудувати її графік.
та побудувати її графік.
Розв’язання. 1) Знайдемо область визначення функції: 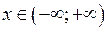 .
.
2) У графіка цієї функції відсутні асимптоти. Якщо функція неперервна, то відсутні вертикальні асимптоти. При знаходженні похилих асимптот  параметр
параметр 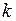 не дорівнює скінченному числу:
не дорівнює скінченному числу:
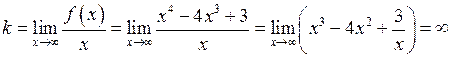 .
.
3) Знайдемо інтервали монотонності та критичні точки функції за допомогою першої похідної.
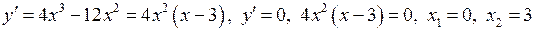 .
.
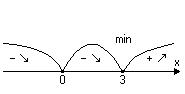 Одержані точки розбивають область визначення функції на такі інтервали:
Одержані точки розбивають область визначення функції на такі інтервали: 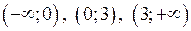 . Знайдемо знак похідної в кожному з інтервалів.
. Знайдемо знак похідної в кожному з інтервалів.
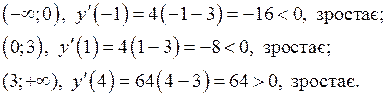
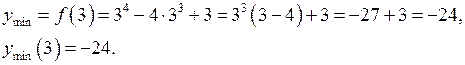
4) Знайдемо інтервали вгнутості та точки перегину графіка функції за допомогою похідної другого порядку.
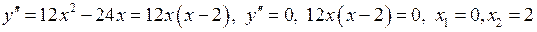 .
.
Критичні точки другого порядку 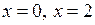 розбивають область визначення функції на інтервали вгнутості. Знайдемо знак другої похідної у кожному з них.
розбивають область визначення функції на інтервали вгнутості. Знайдемо знак другої похідної у кожному з них.
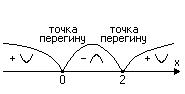
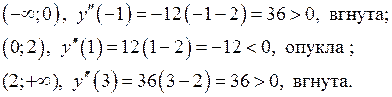
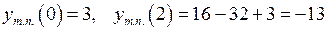 .
.
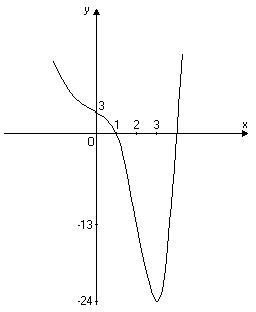 Точки перегину функції мають координати:
Точки перегину функції мають координати: 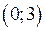 і
і 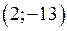 .
.
5) Знайдемо точки перетину функції з осями координат: при 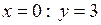 ; при
; при  . Для рівняння
. Для рівняння 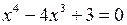 можна методом підбору знайти один корінь
можна методом підбору знайти один корінь  .
.
6) Побудуємо схематично графік функції (рис. 8).
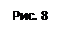
Приклад 20. Провести повне дослідження функції 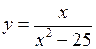 та побудувати її графік.
та побудувати її графік.
Розв’язання. 1) Знайдемо область визначення функції. Необхідно знайти ті точки, в яких знаменник дробу дорівнює нулю і виключити їх. Одержимо  . Функція визначена в інтервалах
. Функція визначена в інтервалах 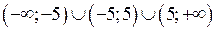 .
.
2) Знайдемо асимптоти графіка функції.
а) Вертикальні асимптоти будемо шукати в точках розриву функції. Одержимо
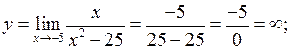
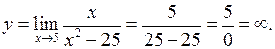
Прямі  та
та  є вертикальними асимптотами функції.
є вертикальними асимптотами функції.
б) Похилі асимптоти будемо шукати у вигляді  , а невідомі параметри
, а невідомі параметри  і
і 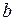 визначимо за формулами (23). Одержимо
визначимо за формулами (23). Одержимо
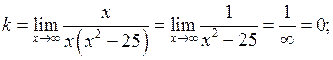
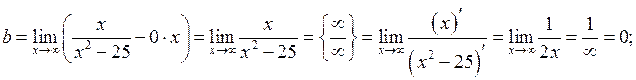
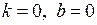 , тоді
, тоді 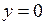 – вісь
– вісь  – похила асимптота.
– похила асимптота.
3) Знайдемо інтервали монотонності та критичні точки функції. Для цього знайдемо першу похідну функції. Маємо:
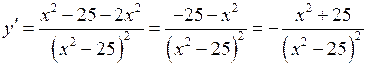 ;
;
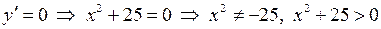 .
.
Тоді 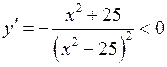 для всіх
для всіх 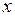 із області неперервності.
із області неперервності.
 Тобто функція спадна на кожному інтервалі області визначення.
Тобто функція спадна на кожному інтервалі області визначення.
4) Знайдемо інтервали вгнутості та точки перегину графіка функції. Для цього знайдемо другу похідну.
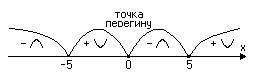
 Прирівняємо
Прирівняємо 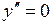 . Одержимо
. Одержимо 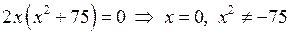 ;
; 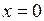 – критична точка.
– критична точка.
Знайдемо знак другої похідної в кожному з інтервалів 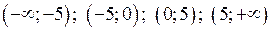 .
.
Маємо 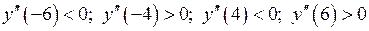 .
.
На інтервалах 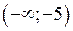 та
та 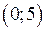 графік опуклий, а на інтервалах
графік опуклий, а на інтервалах  та
та 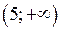 – вгнутий. Точка
– вгнутий. Точка 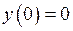 є точкою перегину графіка функції.
є точкою перегину графіка функції.
5) Знайдемо точки перетину графіка функції з осями координат: при 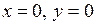 , при
, при 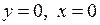 . Інших точок не існує.
. Інших точок не існує.
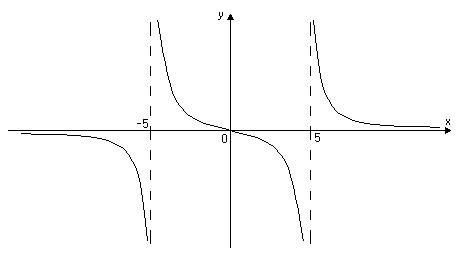 6) Використовуючи результати досліджень, побудуємо графік функції (Рис. 9).
6) Використовуючи результати досліджень, побудуємо графік функції (Рис. 9).
|
|
|
Зауваження. Часто при побудові графіка функції знаходять парність функції. Тобто перевіряють умови: 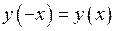 – функція парна та
– функція парна та 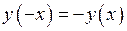 – функція непарна. Якщо жодна умова не виконується, то функція ні парна, ні непарна, а її графік загального положення.
– функція непарна. Якщо жодна умова не виконується, то функція ні парна, ні непарна, а її графік загального положення.
Для функції 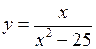 виконується умова
виконується умова
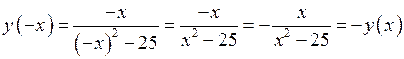 .
.
Функція непарна, а її графік симетричний відносно початку координат.
|
|