
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Генеральная совокупность и частотное распределение
|
|
Фундаментальным понятием математической статистики является понятие группы, или совокупности, которое обычно определяется как генеральная совокупность. Генеральная совокупность — это совокупность, множество элементов, обладающих каким-то одним или многими признаками[119].
Признак является переменной величиной для каждого элемента генеральной совокупности и называется вариантой.
Количественная варианта может быть прерывной (дискретной н непрерывной. Если дана генеральная совокупность N лиц, которые изучаются, например, по своему доходу, то в этом случае варианта (доход) является непрерывной величиной, которая может в определенных пределах принимать любые значения. Если же эти N лиц изучаются по их семейному положению, например, какова величина семьи, в которой живет данный индивид, то в этом случае варианта является величиной прерывной, поскольку она может принимать только целочисленные значения 1, 2, 3... и т.д.
Рассмотрим случай прерывной варианты.
Предположим, что дана генеральная совокупность объема N, каждый элемент которой характеризуется прерывной вариантой Х. Как можно охарактеризовать эту генеральную совокупность по данному признаку (варианте)?
Самый естественный и простой путь — сгруппировать члены генеральной совокупности по всем возможным значениям признака. Сначала группируем элементы генеральной совокупности, имеющие наименьшее значение варианты, а именно значение X1. Затем члены, имеющие значения X2, X3 … и т.д. Наконец, отбираем члены, имеющие наибольшее значение варианты — Xk. Количество членов генеральной совокупности в каждой группе, соответствующей определенному значению варианты, называется частотой варианты X и обозначается через ni.

В результате мы получаем два ряда чисел, которые можно расположить один под другим таким образом:
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
X1 X2 … Xi … Xk
nx n1 n2 … ni … nk
Получилась таблица, которая дает частотное распределение варианты X в генеральной совокупности. Очевидно, что 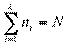 .
.
Иногда частотное распределение представляют графически: на оси X откладывают значение варианты, на оси Y — частоту. Полученные точки соединяют ломаной, которая называется полигоном распределения (рис. 1).
Ломаную принято соединять с осью X в смежных точках оси X, в которых, полагают, частоты равны 0 (в данном случае в точках X0 и Xk+1).
В том случае, если варианта – непрерывная величина, дело несколько усложняется: нельзя непосредственно сгруппировать элементы генеральной совокупности по значениям варианты, поскольку может оказаться, что каждый член имеет свое, отличное от других значение варианты. Тогда поступают следующим образом. Предположим, что все значения варианты находятся на отрезке [a, b]. Этот отрезок разбивают на n равных
частей, которые называют разрядами, интервалами, классами или класс-интервалами. Отбирают члены генеральной совокупности, варианты которых попадают в первый класс-интервал, затем элементы, попавшие во второй класс-интервал, и т.д. вплоть до последнего n-ro класс-интервала. Число элементов генеральной совокупности, попавших в определенный класс-интервал, называется частотой этого класс-интервала. Очевидно, что класс-интервал определяется по формуле
Ä x= 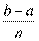
Выбор n зависит от многих причин и должен быть таким, чтобы класс-интервал был не очень малым (чтобы класс-интервалов было не слишком много) и не очень большим (чтобы не исчезла специфика изменения варианты).
Существует ряд приближенных формул для определения не- обходимого Ä х, а также ряд допущений в отношении значений варианты на границах класс-интервалов, за которыми мы отсылаем к соответствующей литературе[120].
Частотное распределение (в случае непрерывной варианты) будет иметь следующий вид:
Класс-интервалы I II III…
Частоты 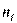
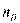
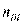 …
…
В класс-интервалы кроме первого и последнего включаются варианты по своему значению больше нижней грани и равные верхней грани или меньше ее и условно принимается, что члены генеральной совокупности, попавшие в данный класс-интер- вал, имеют одинаковую варианту, равную середине данного класс-интервала.
Частотное распределение в случае непрерывной варианты также может быть изображено графически.
На оси Х прямоугольной системы координат отмечаются точки а и b нижней и верхней грани изменения варианты. Определяется класс-интервал. На интервале (а, b) откладываются выбранные класс-интервалы. На каждом класс-интервале как на основании строится прямоугольник с высотой, пропорциональной частоте этого класс-интервала. Верхние основания всех построенных таким образом прямоугольников образуют некоторую ступенчатую линию, называемую гистограммой, ко-
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
торая и является графическим изображением данного частот- ного распределения (рис. 2).
Если соединим середины верхних оснований прямоугольни- ков гистограммы, то получим полигон данного распределения. Тем самым генеральную совокупность непрерывной варианты можно представлять двумя видами графиков — полигоном и гистограммой, а прерывной варианты — только одним видом —
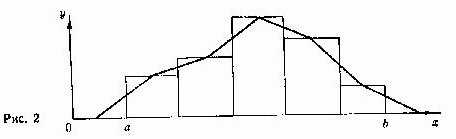
полигоном. Площадь всей гистограммы пропорциональна объе- му генеральной совокупности.
Иногда вместо частоты применяют относительную частоту, равную отношению частоты к объему генеральной совокупности.
Если мы исследуем данную генеральную совокупностЬ по варианте Х, то прежде всего мы получаем частотное распределение, которое может быть представлено в виде таблицы или графика. Полученное в процессе исследования частотное распределение называется эмпирическим распределе- нием.
Возьмем эмпирический полигон какой-либо непрерывной варианты. При достаточно большом объеме генеральной совокупности N будем одновременно увеличивать число и, следовательно, одновременно уменьшать величину класс-интервалов. У полигона будет увеличиваться число все уменьшающихся звеньев, и если продолжать этот процесс до бесконечности, то в пределе полигон перейдет в некоторую гладкую кривую, которая называется кривой распределения.
Каждый полигон эмпирического распределения является некоторым приближением определенной кривой распределения (рис. 3).
Эта кривая распределения, являющаяся предельным случаем полигона данного эмпирического распределения, называется по установившейся терминологии функцией плотности распре- деления и обозначается f (х). Интеграл от нее по области
изменения варианты называется функцией распределения и обозначается

Иногда f(x) и F(x) называют дифференциальным и интегральным законами распределения соответственно.
Возьмем какие-то эмпирические гистограмму и полигон и соответствующую им кривую распределения (рис. 4).


Гистограмма и полигон в пределе стремятся к кривой распределения f(x). По определению гистограммы, частота значений варианты Х равна площади прямоугольников, построенных на класс-интервалах. Частота события по частотному определению вероятности при бесконечном увеличении числа испытаний стремится к вероятности события[121].
Следовательно, для кривой распределения площадь под ней между значениями х, и х, это вероятность того, что варианта
примет значения между  и
и  [122]. Это можно записать таким образом:
[122]. Это можно записать таким образом:
 .
.
Частотные распределения обычно характеризуются двумя типами параметров:
I — параметры положения или средние;
II — параметры или меры рассеивания.
Наибольшее значение имеют три вида средних: средняя арифметическая, медиана и мода.
Средняя арифметическая (М) для прерывной варианты reнеральной совокупности объема N определяется выражением
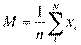
или
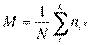
где k — яисло различных значений: варианты Х, а 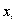 — значения
— значения
варианты.
Для непрерывной варианты Х, изменяющейся в интервале
{а, b} генеральной совокупности объема N,

где f(х) — функция плотности распределения. Иначе говоря, средняя арифметическая есть абсцисса центра тяжести площади фигуры, образованной кривой распределения и осью абсцисс.
Медиана (Me) — это такое значение варианты, когда половина генеральной совокупности имеет значения меньше его, половина — больше.
Геометрически медиана означает абсциссу прямой, которая делит пополам площадь под кривой распределения.
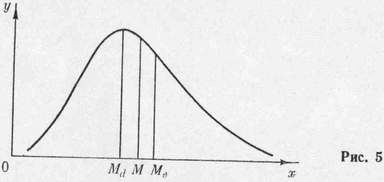
Мода (Md) — значение варианты, соответствующее наибольшей частоте (вероятности). Графически мода — это значение абсциссы самой высокой точки кривой распределения (рис. 5).
Для симметричного распределения средняя арифметическая медиана и мода совпадают.
В качестве меры рассеивания наиболее распространены понятия дисперсии и квадратного корня из дисперсии, который называется стандартом или средним квадратическим отклонением.
Дисперсия есть средний квадрат отклонения варианты от ее среднего арифметического; она обозначается  .
.
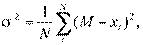
стандарт  :
:

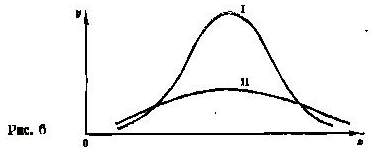
На рис.6 кривая I характеризуется малой дисперсией; кривая II — большой дисперсией.
Наибольшее значение для социологических исследований имеют три теоретических закона распределения.
1) Нормальное распределение, или распределение Гаусса (для непрерывной варианты):


2) Биноминальное распределение, или распределение Бернулли (для прерывной варианты).
Если при каждом испытании вероятность осуществления события есть р, неосуществления — q=1 — р, то вероятность того, что при и испытаниях это событие осуществится т раз, равна
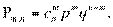
3) Распределение Пуассона, или закон малых чисел, представляет собой предельный случай биноминального распределения: когда 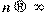 , a
, a 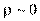 , то, обозначая np=a, имеем
, то, обозначая np=a, имеем
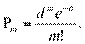
Это распределение имеет место в случае большого числа испытаний маловероятных событий.
|
|
