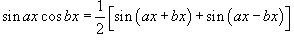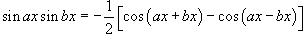Интегрирование некоторых классов тригонометрических функций. Перечислить основные методы и подстановки (без вывода).

Неопределенный интеграл

Интегралы от иррациональных функций. Перечислить основные подстановки

1) Интегралы вида

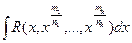
m_1, n₁…m_k, n_k – целые числа

Подстановка x=t⁵,

5=HOK (n_1, …, n_k)

2) Интегралы вида

Подстановка ax+b=t⁵

5=HOK (n₁, …, n_k)

3) Интегралы вида

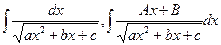
Интегралы от некоторых ф-й содержащих квадратных трех челен

4) Интеграл от дифференциального бинома

Интегралы вида

m, n, p – целые числа

а) p – целое, подстановка x=t⁵, 5=HOK (знаменатели дробей m, n)

б) 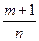- целое, подстановка a+bxⁿ= t⁵, 5 – знаменатель дроби

в) 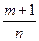+p – целое число

ax^-1+b= t⁵, 5 – знаменатель дроби p

Универсальная тригонометрическая подстановка (вывод)

Тождества имеют смысл, только когда существуют обе части (то есть при ).

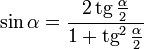
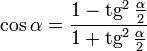
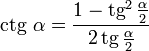
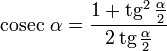
Интегрирование некоторых классов тригонометрических функций. Перечислить основные методы и подстановки (без вывода).

1. Интегралы вида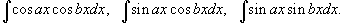

Для решения данных интегралов применяются формулы преобразования произведения тригонометрические функций в сумму или разность:

2. Интегралы вида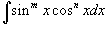

Здесь и везде ниже предполагается, что m и n - натуральные числа. Для вычисления таких интегралов используются следующие подстановки и преобразования:

1. Если степень косинуса n - нечетная (при этом степень синуса m может быть любой), то используется подстановка .
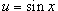2. Если степень синуса m - нечетная, то используется подстановка .
3. Если степени m и n - четные, то сначала применяются формулы двойного угла

чтобы понизить синуса или косинуса в подынтегральном выражении. Затем, если необходимо, применяются правила a) или b).

3. Интегралы вида

Степень подынтегрального выражения в данном интеграле можно понизить с помошью тригонометрического соотношения и формулы редукции

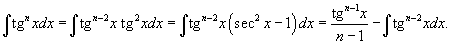
4. Интегралы вида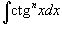

Здесь степень подынтегрального выражения понижается с помошью соотношения 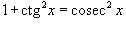и формулы редукции

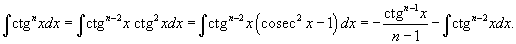
5. Интегралы вида

Данный тип интеграла упрощается с помощью следующей формулы редукции:

6. Интегралы вида

Аналогично предыдущим пунктам, интеграл упрощается с помощью формулы

7. Интегралы вида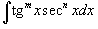

1. Если степень секанса n - четная, то c помошью соотношения секанс выражается через тангенс. При этом множитель 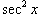отделяется и используется для преобразования дифференциала. В результате весь интеграл (включая дифференциал) выражается через функцию tg x.
2. Если обе степени n и m - нечетные, то отделяется множитель sec x tg x, необходимый для преобразования дифференциала. Далее весь интеграл выражается через sec x.
3. Если степень секанса n - нечетная, а степень тангенса m - четная, то тангенс выражается через секанс с помощью формулы . Затем вычисляются интегралы от секанса.

8. Интегралы вида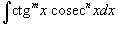

1. Если степень косеканса n - четная, то c помошью соотношения 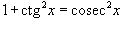косеканс выражается через котангенс. При этом множитель отделяется и используется для преобразования дифференциала. В результате подынтегральная функция и дифференциал выражаются через ctg x.
2. Если обе степени n и m - нечетные, то отделяется множитель ctg x cosec x, необходимый для преобразования дифференциала. Далее интеграл выражается через cosec x.
3. Если степень косеканса n - нечетная, а степень котангенса m - четная, то котангенс выражается через косеканс с помощью формулы 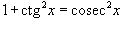. Далее вычисляются интегралы от косеканса.

11. «Неберущиеся» интегралы

Существуют такие элементарные ф-ии первообразные от которых не явл. Элементами ф-ми такие первообразные не только существуют но играют большую роль в математическом анализе его приложений они изучены, для них составлены специальные таблицы и гр-ки помогающие их практическому использованию

Опр. Если первообразная не явл. Элементарной ф-ей то говорят, что интеграл не берется в элементарных ф-ях.