
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задания лабораторной работы 1. 1. Написать файл-функции для решения поставленных далее задач.
|
|
1. Написать файл-функции для решения поставленных далее задач.
2. Сохранить их в отдельных m-файлах (среда Матлаб)
3. Выполнить и оформить в виде отчета поставленные далее задачи.
Задача №1. Написать формулы методов прогонки и пристрелки для решения краевой задачи:
u" (x) - p(x)u'(x) + q(x)u(x) = f(x),
α 0u(a) + α 1u'(a) = A,
β 0u(b) + β 1u'(b) = B.
Решить краевую задачу двумя методами: прогонки и пристрелки.
Варианты заданий в табл.3.
Табл.3.
| № варианта | Дифференциальное уравнение | Начальное условие | [a, b] | N |
| y" (x) – x y(x)=sin(x) | y(0)=1, y(2)=0 | [0, 2] | 10 | |
| y" (x) - 2x2 y(x)=x | y(0)=2, y(2)=1 | [0, 2] | 20 | |
| y" (x) – 3cos(x) y(x)=tg(x) | y(0)=3, y(1)=2 | [0, 1] | 30 | |
| y" (x) – x y(x)=sin2(x) | y(0)=1, y(2)=3 | [0, 2] | 40 | |
| y" (x) - sin(x) y(x)=sin(x) | y(0)=2, y(2)=4 | [0, 2] | 50 | |
| y" (x) - cos(x) y(x)=sin(x) | y(1)=3, y(2)=1 | [1, 2] | 10 | |
| y" (x) - 2x2 y(x)=cos(x) | y(1)=1, y(2)=2 | [1, 2] | 20 | |
| y" (x) – tg(x – 1) y(x)=x | y(1)=2, y(2)=3 | [1, 2] | 30 | |
| y" (x) - sin(x) y(x)=sin3(x) | y(1)=3, y(2)=2 | [1, 2] | 40 | |
| y" (x) – lnx y(x)= sin(x) | y(1)=1, y(2)=0 | [1, 2] | 50 | |
| y" (x)-cos(x) y(x)=x | y(1)=2, y(3)=1 | [1, 3] | 10 | |
| y" (x) - 2x2 y(x)=x2 | y(1)=3, y(3)=2 | [1, 3] | 20 | |
| y" (x) - lgx y(x)=2x | y(1)=1, y(3)=3 | [1, 3] | 30 | |
| y''(x) - 2|sin(x)| y(x)=3x3 | y(1)=2, y(3)=2 | [1, 3] | 40 | |
| y" (x) – 2lnx y(x)=1+x | y(1)=3, y(3)=4 | [1, 3] | 50 | |
| y''(x) - |cos(x)| y(x)=tg(x) | y(-1)=1, y(1)=1 | [-1, 1] | 10 | |
| y" (x) - 2|x| y(x)=cos2(x) | y(-1)=2, y(1)=2 | [-1, 1] | 20 | |
| y" (x) – tg(x) y(x)=e2x | y(-1)=3, y(1)=0 | [-1, 1] | 30 | |
| y" (x) – ln(1+x2) y(x)=sin(2x) | y(-1)=1, y(1)=2 | [-1, 1] | 40 | |
| y" (x) – sin|x| y(x)=sin(x) | y(-1)=2, y(1)=1 | [-1, 1] | 50 | |
| y" (x) – 2y(x)=sin(x) | y(0)=2, y(π)=2 | [0, π ] | 10 | |
| y" (x) – 3y(x)=cos(x) | y(0)=1, y(π)=1 | [0, π ] | 20 | |
| y" (x) - 2x y(x)=x3 | y(0)=2, y(π)=2 | [0, π ] | 30 | |
| y" (x) - x y(x)=x4 | y(0)=3, y(π)=2 | [0, π ] | 40 | |
| y" (x) - 2x2 y(x)=x2 | y(0)=1, y(π)=3 | [0, π ] | 50 | |
| y" (x)+cos(x) y(x)=ex sin(x) | y(π /2)=2, y(π)=4 | [π /2, π ] | 10 | |
| y" (x) - 2x2 y(x)=2x ex | y(π /2)=3, y(π)=2 | [π /2, π ] | 20 | |
| y" (x) - 5y(x)=32x | y(π /2)=1, y(π)=1 | [π /2, π ] | 30 | |
| y" (x) – 2sin(x) y(x)=sin(3x) | y(π /2)=2, y(π)=2 | [π /2, π ] | 40 | |
| y" (x) – lnx y(x)=1 | y(π /2)=3, y(π)=4 | [π /2, π ] | 50 |
Задача №2.
Решить на отрезке [1, 2] задачу Коши:
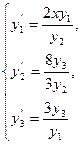
y1(1)=1, y2(1)=2, y3(1)=3.
(Точным решением задачи является система функций y1(x)=x, y2(x)=2x2, y3(x)=3x3)
Задача №3.
Решить задачу Коши для дифференциального уравнения третьего порядка:
y'" =y - y' + y", x є (0, 1),
y(0)=0, y'(0)=1, y" (0)=0.
(Точным решением данной задачи является функция y(x)=sin(x))
Контрольные вопросы:
1. Какое уравнение называется обыкновенным дифференциальным уравнением?
2. Какие методы решения задач для дифференциальных уравнений вы знаете?
3. Какие задачи называются краевыми для обыкновенных дифференциальных уравнений?
|
|
