
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задачи Коши
|
|
При изучении способов решения дифференциальных уравнений приближенными методами основной задачей считается задача Коши.
Рассмотрим наиболее популярный метод решения задачи Коши – метод Рунге-Кутта. Этот метод позволяет строить формулы расчета приближенного решения практически любого порядка точности.
Выведем формулы метода Рунге-Кутта второго порядка точности. Для этого решение представим куском ряда Тейлора, отбрасывая члены с порядком выше второго. Тогда приближенное значение искомой функции в точке x1 можно записать в виде:
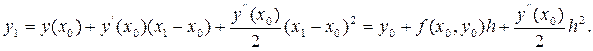 (2)
(2)
Вторую производную y" (x0) можно выразить через производную функции f(x, y), однако в методе Рунге-Кутта вместо производной используют разность
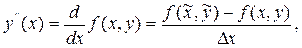
соответственно подбирая значения параметров 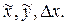
Тогда (2) можно переписать в виде:
y1=y0 + h [β f(x0, y0) + α f(x0 + γ h, y0 + δ h)], (3)
где α, β, γ и δ – некоторые параметры.
Рассматривая правую часть (3) как функцию аргумента h, разложим ее по степеням h:
y1=y0 +(α + β) h f(x0, y0) + α h2[γ fx(x0, y0) + δ fy(x0, y0)],
и выберем параметры α, β, γ и δ так, чтобы это разложение было близко к (2). Отсюда следует, что
α + β =1, α γ =0, 5, α δ =0, 5 f(x0, y0).
С помощью этих уравнений выразим β, γ и δ через параметры α, получим
y1=y0 +h[(1 - α) f(x0, y0) + α f(x0+ 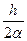 , y0+
, y0+ 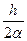 f(x0, y0)], (4)
f(x0, y0)], (4)
0 < α ≤ 1.
Теперь, если вместо (x0, y0) в (4) подставить (x1, y1), получим формулу для вычисления y2 – приближенного значения искомой функции в точке x2.
В общем случае метод Рунге-Кутта применяется на произвольном разбиении отрезка [x0, X] на n частей, т.е. с переменным шагом
x0, x1, …, xn; hi = xi+1 – xi, xn = X. (5)
Параметры α выбирают равными 1 или 0, 5. Запишем окончательно расчетные формулы метода Рунге-Кутта второго порядка с переменным шагом для α =1:
yi+1=yi +hi f(xi + 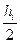 , yi+
, yi+ 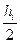 f(xi, yi)), (6.1)
f(xi, yi)), (6.1)
i = 0, 1, …, n-1.
и α =0, 5:
yi+1=yi + 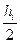 [f(xi, yi) + f(xi+ hi, yi+ hi f(xi, yi))], (6.2)
[f(xi, yi) + f(xi+ hi, yi+ hi f(xi, yi))], (6.2)
i = 0, 1, …, n-1.
Наиболее употребляемые формулы метода Рунге-Кутта – формулы четвертого порядка точности:
yi+1=yi + 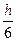 (k1+ 2k2+ 2k3+ k4),
(k1+ 2k2+ 2k3+ k4),
k1=f(xi, yi), k2= f(xi +  , yi+
, yi+  k1), (7)
k1), (7)
k3= f(xi +  , yi+
, yi+  k2), k4= f(xi +h, yi+hk3).
k2), k4= f(xi +h, yi+hk3).
Для метода Рунге-Кутта применимо правило Рунге для оценки погрешности. Пусть y(x; h) – приближенное значение решения в точке x, полученное по формулам (6.1), (6.2) или (7) с шагом h, а p – порядок точности соответствующей формулы. Тогда погрешность R(h) значения y(x; h) можно оценить, используя приближенное значение y(x; 2h) решения в точке x, полученное с шагом 2h:
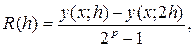 (8)
(8)
где p=2 для формул (6.1) и (6.2) и p=4 для (7).
Уточненное решение пишем в виде
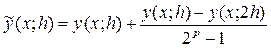 . (9)
. (9)
В алгоритмах с автоматическим выбором шага предварительно задают погрешность в виде положительного параметра ε, и на каждом этапе вычисления следующего значения yi+1 подбирают такой шаг h, при котором выполняется неравенство
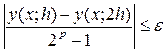 , (10)
, (10)
Метод Рунге-Кутта применим и к задаче Коши для системы m дифференциальных уравнений первого порядка с m неизвестными функциями
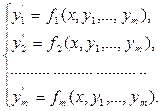 x
x 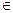 (x0, X), (11)
(x0, X), (11)
y1(x0)=y1, 0, y2(x0)=y2, 0, …, ym(x0)=ym, 0. (12)
Приведем для задачи (11), (12) расчетные формулы метода Рунге-Кутта четвертого порядка. Пусть требуется найти систему m функций y1(x), y2(x), …, ym(x), удовлетворяющих в интервале (x0, X) дифференциальным уравнениям (11), а в точке x0 – начальным условиям (12). Предположим, что отрезок [x0, X] разбит на N частей:
xi= x0+ i hi, 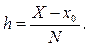
Тогда каждую l -ю функцию yl(x) можно приближенно вычислять в точках xi+1 по формулам Рунге-Кутта
Kl, 1=fl(xi, y1, i, y2, i, …, ym, i), i=1, 2, …, m,
Kl, 2=fl(xi +  , y1, i +
, y1, i +  K1, 1, y2, i +
K1, 1, y2, i +  K2, 1, …, ym, i +
K2, 1, …, ym, i +  Km, 1), i=1, 2, …, m,
Km, 1), i=1, 2, …, m,
Kl, 3=fl(xi +  , y1, i +
, y1, i +  K1, 2, y2, i +
K1, 2, y2, i +  K2, 2, …, ym, i +
K2, 2, …, ym, i +  Km, 2), i=1, 2, …, m, (13)
Km, 2), i=1, 2, …, m, (13)
Kl, 4=fl(xi + h, y1, i + hK1, 3, y2, i + hK2, 3, …, ym, i + hKm, 3), i=1, 2, …, m,
Yl, i+1 = yl, i + 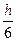 (Kl, 1 + 2 Kl, 2 + 2 Kl, 3 + Kl, 4), i=1, 2, …, m,
(Kl, 1 + 2 Kl, 2 + 2 Kl, 3 + Kl, 4), i=1, 2, …, m,
Здесь через yl, i обозначается приближенное значение функции yl(x) в точке xi.
Обратите внимание на порядок вычислений по формулам (13). На каждом шаге сначала вычисляются коэффициенты Kl, i в следующем порядке:
K1, 1, K2, 1, …, Km, 1,
K1, 2, K2, 2, …, Km, 2,
K1, 3, K2, 3, …, Km, 3,
K1, 4, K2, 4, …, Km, 4,
и лишь затем приближенные значения функций y1, i+1, y2, i+1, …, ym, i+1.
Задачи Коши для дифференциальных уравнений n -го порядка
y(n)=f(x, y, y', …, y(n-1)), x 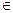 (x0, X), (14)
(x0, X), (14)
y(x0)=y0, y'(x0)=y1, 0, …, y(n-1)(x0)=yn-1, 0 (15)
сводятся к задаче Коши для системы дифференциальных уравнений первого порядка с помощью замены переменных
z0= y, z1= y', …, zn-1= y(n-1). (16)
Учитывая (16), из уравнения (14) получим систему дифференциальных уравнений
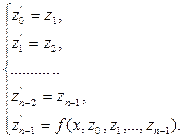 (17)
(17)
Начальные условия (15) для функций zl переписываются в виде
z0(x0)= y0, z1(x0)= y1, 0, …, zn-1(x0)= yп-1, 0. (18)
Запишем для полученной системы метод Рунге-Кутта:
zl, i+1= zl, i + 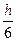 (Kl, 1+ 2Kl, 2+ 2Kl, 3+ Kl, 4), (19)
(Kl, 1+ 2Kl, 2+ 2Kl, 3+ Kl, 4), (19)
i=0, 1, …, N, l=0, 1, …, n-1.
Для вычисления коэффициентов Kl, 1, Kl, 2, Kl, 3 и Kl, 4 имеем следующие формулы:
K0, 1=z1, i,
K1, 1=z2, i,
…………
Kn-1, 1= f(xi, z0, i, z1, i, …, zn-1, i,),
K0, 2= z1, i+  K1, 1,
K1, 1,
K1, 2= z2, i+  K2, 1,
K2, 1,
…………………
Kn-1, 2= f(xi+  , z0, i+
, z0, i+  K0, 1, z1, i+
K0, 1, z1, i+  K1, 1, …, zn-1, i+
K1, 1, …, zn-1, i+  Kn-1, 1),
Kn-1, 1),
K0, 3= z1, i+  K1, 2,
K1, 2,
K1, 3= z2, i+  K2, 2,
K2, 2,
……………………
Kn-1, 3= f(xi+  , z0, i+
, z0, i+  K0, 2, z1, i+
K0, 2, z1, i+  K1, 2, …, zn-1, i+
K1, 2, …, zn-1, i+  Kn-1, 2),
Kn-1, 2),
K0, 4= z1, i+ hK1, 3,
K1, 4= z2, i+ hK2, 3,
……………………
Kn-1, 4= f(xi+ h, z0, i+ hK0, 2, z1, i+ hK1, 2, …, zn-1, i+ hKn-1, 2).
|
|