
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Точки, в которых или вторая производная в этих точках не существует, называются критическими точками второго рода.
|
|
Достаточные условия существования точки перегиба.
Если при переходе через критическую точку слева направо вторая производная меняет знак, то имеется перегиб; если перемены знака нет, то перегиба нет.
Пример. Найти интервалы выпуклости, вогнутости и точки перегиба функции y= 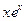 .
.
Решение. Найдем область определения функции. D(f) =(-¥, +¥)
Найдем вторую производную 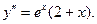 Найдем критические точки второго рода.
Найдем критические точки второго рода. 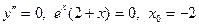 - критическая точка.
- критическая точка.
| х | (-¥, -2) | -2 | (-2, +¥) |
| y” | - | + | |
| y | выпукла | Пер. | вогнута |
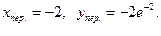 (-2, -2
(-2, -2 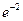 ) – точка перегиба.
) – точка перегиба.
(-¥, -2) - интервал выпуклости, (-2, +¥) - интервал вогнутости.
Асимптоты графика функции.
При исследовании функции необходимо установить ее поведение при удалении текущей точки графика функции от начала координат. В некоторых случаях это можно сделать с помощью прямой, к которой неограниченно приближается текущая точка графика функции при удалении ее от начала координат.
Асимптотой графика функции y = f(x) называется прямая, расстояние от которой до текущей точки графика функции стремится к нулю при неограниченном удалении ее от начала координат.
Различают вертикальные, горизонтальные и наклонные асимптоты. Пусть М(х, у) – текущая точка графика функции. Точка М (х, у) может удаляться от начала координат следующим образом:
1) х® а, у® ¥; 2) х®¥, у® b, 3) x®¥, y®¥.
В первом случае имеем 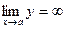 , и прямая x = a является вертикальной асимптотой.
, и прямая x = a является вертикальной асимптотой.
Во втором случае 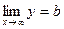 и прямая y = b будет горизонтальной асимптотой.
и прямая y = b будет горизонтальной асимптотой.
В третьем случае график функции y = f(x) имеет наклонную асимптоту, уравнение которой имеет вид y = kx +b.
Необходимое и достаточное условие существование невертикальных асимптот устанавливается с помощью теоремы:
Теорема. Для того чтобы прямая y = kx +b была асимптотой графика функции  , необходимо и достаточно существование пределов
, необходимо и достаточно существование пределов

Если не существует хотя бы один из пределов, то невертикальных асимптот нет.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Пример. Найти асимптоты графика функции 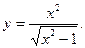
Решение. Точки х = 1 и х = -1 являются точками разрыва второго рода данной функции. Так как  и
и 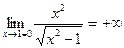 , то прямые
, то прямые  являются вертикальными асимптотами.
являются вертикальными асимптотами.
Найдем невертикальные асимптоты. При 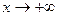 получаем
получаем
 ,
, 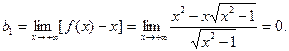
Следовательно, правой асимптотой является прямая у = х.
Аналогично, при 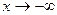 имеем.
имеем.
 ,
, 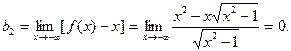
Левой асимптотой графика функции является прямая у = - х
Литература: К.А. Хасеинов Каноны математики. Стр.204-209
Практическое занятие 8
Найти интервалы монотонности и экстремумы функций:
1. 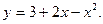
Отв. A)  убывает,
убывает, 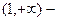 возрастает,
возрастает, 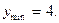
B)  возрастает,
возрастает,  убывает,
убывает, 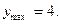
C)  возрастает,
возрастает, 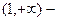 убывает,
убывает, 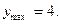
D) 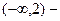 возрастает,
возрастает,  убывает,
убывает, 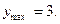
E)  возрастает,
возрастает, 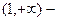 убывает,
убывает, 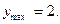
2. 
Отв. A) 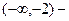 убывает,
убывает, 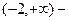 возрастает,
возрастает, 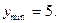
B)  возрастает,
возрастает,  убывает,
убывает, 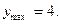
C) 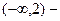 возрастает,
возрастает,  убывает,
убывает, 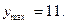
D) 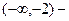 возрастает,
возрастает, 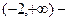 убывает,
убывает, 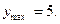
E)  возрастает,
возрастает, 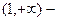 убывает,
убывает, 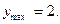
3. 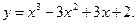
Отв. A) 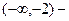 убывает,
убывает, 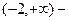 возрастает,
возрастает, 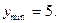
B)  возрастает,
возрастает,  убывает,
убывает, 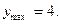
C) 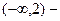 возрастает,
возрастает,  убывает,
убывает, 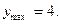
D) 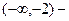 возрастает,
возрастает, 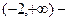 убывает,
убывает, 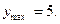
E) 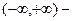 интервал возрастания, экстремумов нет.
интервал возрастания, экстремумов нет.
4. 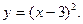 5.
5. 
6. 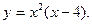
Отв. A) 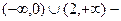 убывает, (0, 2) – возрастает,
убывает, (0, 2) – возрастает, 
B) 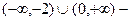 возрастает, (-2, 0) – убывает,
возрастает, (-2, 0) – убывает, 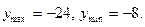
C) 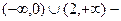 возрастает, (0, 2) – убывает,
возрастает, (0, 2) – убывает, 
D)  возрастает, (0, 3) – убывает,
возрастает, (0, 3) – убывает, 
E) 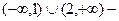 возрастает, (1, 2) – убывает,
возрастает, (1, 2) – убывает, 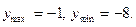
7. 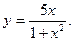 8.
8. 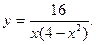
9. 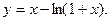 10.
10. 
11. 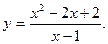 12.
12. 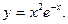
Найти интервалы выпуклости и вогнутости и точки перегиба графиков функции:
1. 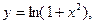 2.
2. 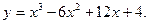
3.  4.
4. 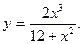
5.  6.
6. 
7. 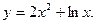 8.
8. 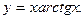
Найти асимптоты графика функции.
1. 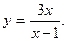 2.
2. 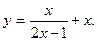
3. 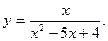 4.
4. 
5. 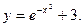 6.
6. 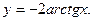
7.  8.
8. 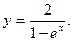
9.  10.
10. 
Пример. Исследовать функцию 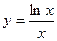 и построить ее график.
и построить ее график.
Решение. 1) Функция определена при х > 0. (0, +¥) – область определения.
2). Исследуем поведение функции на границе области определения.
3) Из предыдущего пункта следует, что прямая х = 0 является вертикальной асимптотой, а прямая у = 0 – горизонтальной асимптотой. Будем находить невертикальные асимптоты y = kx +b.
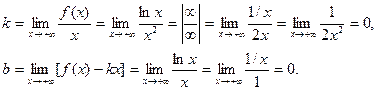
Так как 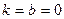 , то наклонной асимптоты нет; прямая у = 0 – горизонтальная асимптота.
, то наклонной асимптоты нет; прямая у = 0 – горизонтальная асимптота.
4) Найдем точку пересечения c осью О х. Если у = 0, то  Точка Р (1; 0) есть точка пересечения графика функции с осью О х.
Точка Р (1; 0) есть точка пересечения графика функции с осью О х.
5) Функция 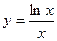 будет функцией общего вида, так как область определения функции не является симметричной относительно начала координат, и поэтому не выполняются условия четности и нечетности функции. Функция непериодическая.
будет функцией общего вида, так как область определения функции не является симметричной относительно начала координат, и поэтому не выполняются условия четности и нечетности функции. Функция непериодическая.
6) Для нахождения интервалов монотонности и экстремумов функции найдем критические точки. Для этого найдем первую производную 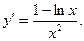
Решив уравнение 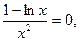 найдем критические точки, подозрительные на экстремум.
найдем критические точки, подозрительные на экстремум. 
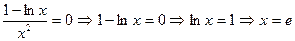 - критическая точка.
- критическая точка.
Исследуем знак первой производной при переходе через критическую точку в сторону возрастания х. Результаты исследования представим в виде таблицы.
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
| х | (0, e) | e | (e, ¥) |
| y’ | + | - | |
  у у
| возрастает | max | убывает |
 ,
, 

 - интервал возрастания,
- интервал возрастания, 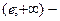 интервал убывания.
интервал убывания.
6) Для нахождения интервалов выпуклости и вогнутости и исследования на перегиб найдем вторую производную. 
Решив уравнение 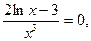 найдем критические точки второго рода.
найдем критические точки второго рода.
 критическая точка второго рода.
критическая точка второго рода.
Исследуем знак второй производной при переходе через критическую точку в сторону возрастания х. Результаты исследования представим в виде таблицы.
| х | (0, 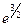 ) )
| 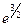
| 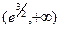
|
| y ” | 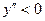
| 
| |
| y | выпуклый | Пере-гиб | вогнутый |

 точка перегиба графика функции.
точка перегиба графика функции.

 8) Используя результаты исследования, строим график функции
8) Используя результаты исследования, строим график функции

 у
у

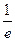




O 1 e 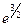 x
x
|
|
