💸 Как сделать бизнес проще, а карман толще?

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое раписание, но и напоминать клиентам о визитах тоже. Проблема в том, что средняя цена по рынку за такой сервис — 800 руб/мес или почти 15 000 руб за год. И это минимальный функционал. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!

Понятие функции.

Тема 2.2. Числовая функция. Ее свойства и график.

Понятие функции.

Пусть рассматриваются два множества X и Y. Правило f, которое ставит в соответствие каждому x∈ X единственный элемент y∈ Y, назовем функцией, заданной на множестве X и принимающей значения на множестве Y.

Функция – правило f, которое каждому элементу x∈ X ставит в соответствие единственный элемент y∈ Y. При этом используют запись у = f(x).

Слово «функция» образовано от латинского functio, что означает исполнение, осуществление.

Переменную х называют независимой переменной или аргументом, а переменную у – зависимой переменной. Говорят, что у является функцией от х.

Значение у, соответствующее заданному значению х, называют значением функции.

Все значения, которые принимает независимая переменная, образуют область определения функции; все значения, которые принимает зависимая переменная, образуют множество значений функции.

Для функции f приняты обозначения: D(f) – область определения функции, E(f) – множество значений функции, f(x₀) – значение функции в точке х_{0 .}

Есл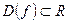и и 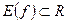, то функцию называют числовой.

Элементы множества 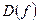так же называют значениями аргумента, а соответствующие им элементы 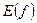– значениями функции.