
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Правило Лопіталя
|
|
ЗАНЯТТЯ № _____
Предмет вищаматематика
Тема: Застосування диференціального числення до дослідження функцій та побудова їх графіків в економіці
Вид заняття лекція
Мета:
навчальна – познайомити студентівіз основні теореми диференціального числення та познайомити із застосуванням диференціальне числення до дослідження функцій та побудови їх графіків;
виховна – виховувати дисциплінованість, наполегливість, любов до предмету.
Література:
[1]Соколенко О.І. Вища математика
[2] Вища математика. Конспект лекцій. Частина І. Укладач Осафійчук М.М.
[3] Рудницький В.Б. Вища математика.
Хід заняття
І. Організаційний момент.
ІІ. Актуалізація опорних знань
1. Сформулюйте означення похідної.
2. Сформулюйте означення диференціала.
3. Сформулюйте основні правила диференціювання функцій.
ІІІ. Викладання нового матеріалу
Основні теореми диференціального числення
Правило Лопіталя
Нехай функції f(x) і g(x):
1) диференційовані в деякому околі точки а і в цьому околі g'(x) ≠ 0;
2) одночасно є нескінченно малими або нескінченно великими в точці а;
3) існує границя відношення похідних цих функцій 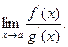
Тоді існує границя відношення цих функцій 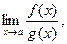 причому
причому 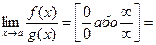
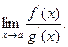
Приклад. За правилом Лопіталя знайти 
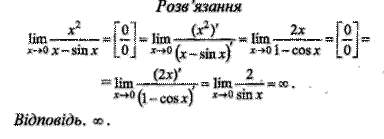
Теорема Ферма. Якщо диференційована функція у = f(x) у деякій точці С інтервалу (а, b) набуває свого найбільшого або найменшого значення, то в цій точці похідна дорівнює нулю: f’ (С) = 0.
Теорема Ролля. Нехай задано функцію у = f (х), неперервну на відрізку [а, b] і диференційовану на інтервалі (а, b). Тоді, якщо f(a) - f(b), то всередині відрізка [а, b] знайдеться точка C (a< C< b), така що f’(C)= 0.
Теорема Лагранжа (про скінченні прирости функції). Нехай задано функцію y = f(x), неперервну на відрізку [а, b] і диференційовану на інтервалі (а, b). Тоді знайдеться точка  , (а<
, (а<  < b), така що похідна функції в цій точці f’ '(
< b), така що похідна функції в цій точці f’ '( ) дорівнюватиме відношенню
) дорівнюватиме відношенню 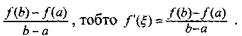
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Теорема Коші (про кінцеві прирости двох функцій). Нехай на відрізку [а, b] задано дві функції f (x)і φ (x). Якщо ці функції неперервні на відрізку [а, b] і диференційовані на інтервалі (а, b), причому φ ’(x) ≠ 0, то на інтервалі (а, b) існує точка  (а <
(а <  < b), така що
< b), така що 
|
|
