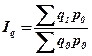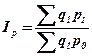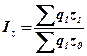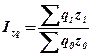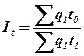| 2. Методы измерения тесноты корреляционной связи в многофакторных моделях
При проведении многофакторного корреляционного анализа возникает необходимость расчета множественных, парных и частных коэффициентов корреляции. Для измерения тесноты корреляционной связи между результативным признаком и несколькими факторными при линейной форме связи рассчитывается множественный коэффициент корреляции по формуле:
Множественный коэффициенткорреляции изменяется от 0 до +1, он показывает тесноту корреляционной связи между результативным признаком и факторными признаками, включенными в уравнение множественной регрессии.
Парные коэффициенты корреляции вычисляются по формулам:
Парные коэффициенты корреляциипоказывают тесноту корреляционной связи как между факторными и результативными признаками, так и между признаками-факторами.
Для исследования тесноты корреляционной связи между признаками при построении моделей множественной регрессии применяются частные (парные) коэффициенты корреляции, которые характеризуют тесноту корреляционной связи между факторными и результативным признаками, при элиминировании влияния учтенных факторов.
Частные коэффициенты корреляции вычисляются по формулам:
Теоретическое корреляционное отношение и совокупный индекс корреляции. Эти показатели имеют такой же экономический смысл, что и при парной регрессии, и определяются по формулам:
Вместо теоретического корреляционного отношения может быть использован адекватный ему показатель – совокупный индекс корреляции:
Проверка адекватности многофакторной регрессионной модели
Построенное уравнение множественной регрессии необходимо содержательно интерпретировать и оценивать его с точки зрения адекватности реальной действительности.
Для оценки адекватности модели можно вычислить отклонение теоретических данных от эмпирических, остаточную дисперсию, а также ошибку аппроксимации, которая определяется по формуле:
Особое внимание необходимо обратить на интерпретацию и оценку параметров уравнения. Параметры уравнения регрессии следует проверить на их значимость. Для оценки значимости параметров при малых выборках уравнения множественной регрессии используются t-критерий Стьюдента при (n – m - 1) степенях свободы:
Адекватность уравнения регрессии оценивается с помощью F-критерия Фишера, который определяется по формуле:
Существенность совокупного коэффициента корреляции также оценивается с
помощью t-критерия Стьюдента:
9.6. Непараметрические показатели связи
Коэффициент Фехнера
Коэффициент Спирмена
Коэффициент конкордации
Коэффициенты ассоциации и контингенции
|
|
Тема: 10.Экономические индексы
10.1. Понятие экономических индексов и их классификация
10.2. Индивидуальные индексы
10.3. Агрегатные индексы
10.4. Средние индексы
10.5.Система базисных и цепных индексов. Индексы с постоянными и переменными весами
10.6. Индексы по составу явления
10.7. Территориальные индексы
10.8. Индексы Ласпейреса, Пааше и Фишера
10.9. Изучение взаимосвязи экономических индексов
10.1. Понятие экономических индексов и их классификация.
Индекс
Классификация индексов:
· - По степени охвата явления
·
· По базе сравнения выделяют
· По виду весов различают
· В зависимости от формы построения
· По характеру объекта исследования
· По составу явления выделяют
· По периоду исчисления
Основные обозначения:
· 10.2. Индивидуальные индексы
Индивидуальные индексы
Индивидуальные индексы служат для характеристики изменения отдельных элементов сложного явления. В зависимости от экономического назначения индивидуальные индексы бывают: физического объема продукции, себестоимости, цен, трудоемкости и т.д.
Индекс физического объема продукции:
показывает, во сколько раз возрос (уменьшился) выпуск какого-либо одного товара в отчетном периоде по сравнению с базисным, или сколько процентов составляет.
Индивидуальный индекс цен:
характеризует изменение цены одного определенного товара в текущем периоде по сравнению с базисным.
Индивидуальный индекс себестоимости единицы продукции:
показывает изменение себестоимости единицы продукции.
Общие индексы строят для количественных (объемных) и качественных показателей. В зависимости от цели исследования и наличия исходных данных используют различные формы построения общих индексов: агрегатная или средневзвешенная.
10.3. Агрегатные индексы.
Агрегатный индекс
Особенность этой формы индекса состоит в том, что непосредственно сравниваются две суммы одноименных показателей.
Индексируемая величина
Вес индекса
При выборе веса индекса следует руководствоваться правилом:
Индекс стоимости продукции (товарооборота) (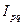 ) - представляет собой отношение стоимости продукции текущего периода к стоимости продукции в базисном периоде. Стоимость продукции – это произведение количества продукции в натуральном выражении (q) на цену (p).
Показывает, во сколько раз возросла (уменьшилась) стоимость продукции отчетного периода по сравнению с базисным, или сколько процентов составляет.
Индекс физического объема продукции – это индекс количественного показателя. Индексируемой величиной будет количество продукции, а весом – цена.
показывает, во сколько раз возросла (уменьшилась) стоимость продукции из-за изменения объемов ее производства.
Разность числителя и знаменателя ( ) - представляет собой отношение стоимости продукции текущего периода к стоимости продукции в базисном периоде. Стоимость продукции – это произведение количества продукции в натуральном выражении (q) на цену (p).
Показывает, во сколько раз возросла (уменьшилась) стоимость продукции отчетного периода по сравнению с базисным, или сколько процентов составляет.
Индекс физического объема продукции – это индекс количественного показателя. Индексируемой величиной будет количество продукции, а весом – цена.
показывает, во сколько раз возросла (уменьшилась) стоимость продукции из-за изменения объемов ее производства.
Разность числителя и знаменателя ( ) показывает, на сколько рублей изменилась стоимость продукции в результате изменения объема.
Индекс цен – это индекс качественного показателя. Индексируемой величиной будет цена товара, т.к. этот индекс характеризует изменение цен. Весом будет выступать количество произведенного товаров.
в числителе – фактическая стоимость продукции текущего периода, а в знаменателе – условная стоимость тех же товаров ценах базисного периода. Показывает, во сколько раз возросла (уменьшилась) стоимость продукции из-за изменения цен. Разность числителя и знаменателя – на сколько рублей изменилась стоимость продукции в результате роста (снижения) цен.
Стоимость продукции можно представить как произведение количества товара на его цену. Точно такая же связьсуществует и между индексами стоимости, физического объема и цен, т.е.
Разность числителя и знаменателя каждого индекса-сомножителя выражает размер изменения общей абсолютной величины под влиянием изменения одного фактора.
Все виды общих индексов в агрегатной форме представлены в табл. 10.1.
10.4. Средние индексы.
Средний индекс
При исчислении средних индексов используются две формы средних: арифметическая и гармоническая.
Арифметическая форма индекса используется сводных индексов количественных показателей, а гармоническая форма индекса – для расчета сводных индексов качественных показателей.
Например, средний арифметический индекс объема продукции вычисляется:
Средний гармонический индекс себестоимости можно исчислить так:
.
Индекс цен:
Индекс Доу-Джонса
Индекс Стэндарда и Пура (Standart and Poor's 500 Stock Index)
Система базисных и цепных индексов.
Индексы с постоянными и переменными весами.
Системой индексов
Система базисных индексов
Система цепных индексов
Система индексов стоимости имеет следующий вид:
· цепные индексы
· базисные индексы
Системой индексов с постоянными весами
Эти индексы строятся, как правило, для количественных показателей (например, индекс физического объема):
· базисные индексы
· цепные индексы
Система индексов с переменными весами
Поэтому эти индексы строятся, как правило, для качественных показателей (например, индекс цен):
· базисные индексы
· цепные индексы
Связь между цепными и базисными индексами
10.6. Индексы по составу явления
Изменение средней величины показателя зависит от двух факторов – изменения значения индексируемого показателя у отдельных единиц и изменения структуры явления.
Изменение структуры – это изменение доли отдельных групп единиц совокупности в общей их численности.
Индекс переменного состава – индекс, выражающий соотношение средних уровней изучаемого явления, относящихся в разным периодам времени. Например, индекс переменного состава стоимости продукции:
Отражает изменение не только изменение индексируемой величины (в данном случае, цены единицы продукции), но и структуры совокупности весов (объем).
Индекс постоянного состава – это индекс, исчисленный с весами, зафиксированными на уровне одного какого-либо периода, и показывающий изменение только индексируемой величины. Например, индекс фиксированного состава стоимости продукции:
Индекс структурных сдвигов – индекс, характеризующий влияние изменения структуры изучаемого явления на динамику среднего уровня этого явления:
Система взаимосвязанных индексов при анализе динамики средней цены имеет следующий вид:
10.7. Территориальные индексы
При построении территориальных индексов приходится решать вопрос, какие веса использовались при их исчислении. При сравнении цен двух стран (А и В) можно построить два индекса:
Формула Эджворта (индекс со стандартными весами):
10.8. Индексы Ласпейреса, Пааше и Фишера
В рыночном хозяйстве особое место уделяется индексу цен (оценка динамики цен, общий измеритель инфляции при макроэкономических исследованиях, установленных ставок налогов). До начала 90-х годов XX века отечественная статистика отдавала предпочтение индексу Пааше. Сложность его расчета заключается в том, что взвешивание по весам отчетного периода требует текущего сбора и обработки значительных объемов информации для формирования системы весов. Это связано с большими затратами различных видов ресурсов. Поэтому, начиная с 1991г. отечественная статистика определяет индекс цен по формуле Ласпейреса, которой отдается предпочтение и в зарубежной статистике.
Основным назначением индекса цен является оценка динамики цен на товары производственного и непроизводственного потребления. В практике статистике используются два основных вида формул индекса цен. Это формулы Ласпейреса и Пааше. ) показывает, на сколько рублей изменилась стоимость продукции в результате изменения объема.
Индекс цен – это индекс качественного показателя. Индексируемой величиной будет цена товара, т.к. этот индекс характеризует изменение цен. Весом будет выступать количество произведенного товаров.
в числителе – фактическая стоимость продукции текущего периода, а в знаменателе – условная стоимость тех же товаров ценах базисного периода. Показывает, во сколько раз возросла (уменьшилась) стоимость продукции из-за изменения цен. Разность числителя и знаменателя – на сколько рублей изменилась стоимость продукции в результате роста (снижения) цен.
Стоимость продукции можно представить как произведение количества товара на его цену. Точно такая же связьсуществует и между индексами стоимости, физического объема и цен, т.е.
Разность числителя и знаменателя каждого индекса-сомножителя выражает размер изменения общей абсолютной величины под влиянием изменения одного фактора.
Все виды общих индексов в агрегатной форме представлены в табл. 10.1.
10.4. Средние индексы.
Средний индекс
При исчислении средних индексов используются две формы средних: арифметическая и гармоническая.
Арифметическая форма индекса используется сводных индексов количественных показателей, а гармоническая форма индекса – для расчета сводных индексов качественных показателей.
Например, средний арифметический индекс объема продукции вычисляется:
Средний гармонический индекс себестоимости можно исчислить так:
.
Индекс цен:
Индекс Доу-Джонса
Индекс Стэндарда и Пура (Standart and Poor's 500 Stock Index)
Система базисных и цепных индексов.
Индексы с постоянными и переменными весами.
Системой индексов
Система базисных индексов
Система цепных индексов
Система индексов стоимости имеет следующий вид:
· цепные индексы
· базисные индексы
Системой индексов с постоянными весами
Эти индексы строятся, как правило, для количественных показателей (например, индекс физического объема):
· базисные индексы
· цепные индексы
Система индексов с переменными весами
Поэтому эти индексы строятся, как правило, для качественных показателей (например, индекс цен):
· базисные индексы
· цепные индексы
Связь между цепными и базисными индексами
10.6. Индексы по составу явления
Изменение средней величины показателя зависит от двух факторов – изменения значения индексируемого показателя у отдельных единиц и изменения структуры явления.
Изменение структуры – это изменение доли отдельных групп единиц совокупности в общей их численности.
Индекс переменного состава – индекс, выражающий соотношение средних уровней изучаемого явления, относящихся в разным периодам времени. Например, индекс переменного состава стоимости продукции:
Отражает изменение не только изменение индексируемой величины (в данном случае, цены единицы продукции), но и структуры совокупности весов (объем).
Индекс постоянного состава – это индекс, исчисленный с весами, зафиксированными на уровне одного какого-либо периода, и показывающий изменение только индексируемой величины. Например, индекс фиксированного состава стоимости продукции:
Индекс структурных сдвигов – индекс, характеризующий влияние изменения структуры изучаемого явления на динамику среднего уровня этого явления:
Система взаимосвязанных индексов при анализе динамики средней цены имеет следующий вид:
10.7. Территориальные индексы
При построении территориальных индексов приходится решать вопрос, какие веса использовались при их исчислении. При сравнении цен двух стран (А и В) можно построить два индекса:
Формула Эджворта (индекс со стандартными весами):
10.8. Индексы Ласпейреса, Пааше и Фишера
В рыночном хозяйстве особое место уделяется индексу цен (оценка динамики цен, общий измеритель инфляции при макроэкономических исследованиях, установленных ставок налогов). До начала 90-х годов XX века отечественная статистика отдавала предпочтение индексу Пааше. Сложность его расчета заключается в том, что взвешивание по весам отчетного периода требует текущего сбора и обработки значительных объемов информации для формирования системы весов. Это связано с большими затратами различных видов ресурсов. Поэтому, начиная с 1991г. отечественная статистика определяет индекс цен по формуле Ласпейреса, которой отдается предпочтение и в зарубежной статистике.
Основным назначением индекса цен является оценка динамики цен на товары производственного и непроизводственного потребления. В практике статистике используются два основных вида формул индекса цен. Это формулы Ласпейреса и Пааше.
|
|

 , то
, то . Знаки коэффициентов регрессии и корреляции см. в таблице:
. Знаки коэффициентов регрессии и корреляции см. в таблице: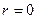

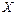 увеличивается
увеличивается 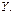
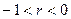
 уменьшается
уменьшается  и наоборот
и наоборот

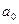 и
и 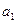 оценивается с
помощью t-критерия Стьюдента
оценивается с
помощью t-критерия Стьюдента 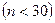 :
Аналогично проводится оценка коэффициента корреляции r с помощью
t- критерия, который определяется по формуле:
Задача: Имеются выборочные данные по 10 однородным предприятиям:
:
Аналогично проводится оценка коэффициента корреляции r с помощью
t- критерия, который определяется по формуле:
Задача: Имеются выборочные данные по 10 однородным предприятиям:
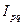 ) - представляет собой отношение стоимости продукции текущего периода к стоимости продукции в базисном периоде. Стоимость продукции – это произведение количества продукции в натуральном выражении (q) на цену (p).
Показывает, во сколько раз возросла (уменьшилась) стоимость продукции отчетного периода по сравнению с базисным, или сколько процентов составляет.
Индекс физического объема продукции – это индекс количественного показателя. Индексируемой величиной будет количество продукции, а весом – цена.
показывает, во сколько раз возросла (уменьшилась) стоимость продукции из-за изменения объемов ее производства.
Разность числителя и знаменателя (
) - представляет собой отношение стоимости продукции текущего периода к стоимости продукции в базисном периоде. Стоимость продукции – это произведение количества продукции в натуральном выражении (q) на цену (p).
Показывает, во сколько раз возросла (уменьшилась) стоимость продукции отчетного периода по сравнению с базисным, или сколько процентов составляет.
Индекс физического объема продукции – это индекс количественного показателя. Индексируемой величиной будет количество продукции, а весом – цена.
показывает, во сколько раз возросла (уменьшилась) стоимость продукции из-за изменения объемов ее производства.
Разность числителя и знаменателя ( ) показывает, на сколько рублей изменилась стоимость продукции в результате изменения объема.
Индекс цен – это индекс качественного показателя. Индексируемой величиной будет цена товара, т.к. этот индекс характеризует изменение цен. Весом будет выступать количество произведенного товаров.
в числителе – фактическая стоимость продукции текущего периода, а в знаменателе – условная стоимость тех же товаров ценах базисного периода. Показывает, во сколько раз возросла (уменьшилась) стоимость продукции из-за изменения цен. Разность числителя и знаменателя – на сколько рублей изменилась стоимость продукции в результате роста (снижения) цен.
Стоимость продукции можно представить как произведение количества товара на его цену. Точно такая же связьсуществует и между индексами стоимости, физического объема и цен, т.е.
Разность числителя и знаменателя каждого индекса-сомножителя выражает размер изменения общей абсолютной величины под влиянием изменения одного фактора.
Все виды общих индексов в агрегатной форме представлены в табл. 10.1.
10.4. Средние индексы.
Средний индекс
При исчислении средних индексов используются две формы средних: арифметическая и гармоническая.
Арифметическая форма индекса используется сводных индексов количественных показателей, а гармоническая форма индекса – для расчета сводных индексов качественных показателей.
Например, средний арифметический индекс объема продукции вычисляется:
Средний гармонический индекс себестоимости можно исчислить так:
.
Индекс цен:
Индекс Доу-Джонса
Индекс Стэндарда и Пура (Standart and Poor's 500 Stock Index)
Система базисных и цепных индексов.
Индексы с постоянными и переменными весами.
Системой индексов
Система базисных индексов
Система цепных индексов
Система индексов стоимости имеет следующий вид:
· цепные индексы
· базисные индексы
Системой индексов с постоянными весами
Эти индексы строятся, как правило, для количественных показателей (например, индекс физического объема):
· базисные индексы
· цепные индексы
Система индексов с переменными весами
Поэтому эти индексы строятся, как правило, для качественных показателей (например, индекс цен):
· базисные индексы
· цепные индексы
Связь между цепными и базисными индексами
10.6. Индексы по составу явления
Изменение средней величины показателя зависит от двух факторов – изменения значения индексируемого показателя у отдельных единиц и изменения структуры явления.
Изменение структуры – это изменение доли отдельных групп единиц совокупности в общей их численности.
Индекс переменного состава – индекс, выражающий соотношение средних уровней изучаемого явления, относящихся в разным периодам времени. Например, индекс переменного состава стоимости продукции:
Отражает изменение не только изменение индексируемой величины (в данном случае, цены единицы продукции), но и структуры совокупности весов (объем).
Индекс постоянного состава – это индекс, исчисленный с весами, зафиксированными на уровне одного какого-либо периода, и показывающий изменение только индексируемой величины. Например, индекс фиксированного состава стоимости продукции:
Индекс структурных сдвигов – индекс, характеризующий влияние изменения структуры изучаемого явления на динамику среднего уровня этого явления:
Система взаимосвязанных индексов при анализе динамики средней цены имеет следующий вид:
10.7. Территориальные индексы
При построении территориальных индексов приходится решать вопрос, какие веса использовались при их исчислении. При сравнении цен двух стран (А и В) можно построить два индекса:
Формула Эджворта (индекс со стандартными весами):
10.8. Индексы Ласпейреса, Пааше и Фишера
В рыночном хозяйстве особое место уделяется индексу цен (оценка динамики цен, общий измеритель инфляции при макроэкономических исследованиях, установленных ставок налогов). До начала 90-х годов XX века отечественная статистика отдавала предпочтение индексу Пааше. Сложность его расчета заключается в том, что взвешивание по весам отчетного периода требует текущего сбора и обработки значительных объемов информации для формирования системы весов. Это связано с большими затратами различных видов ресурсов. Поэтому, начиная с 1991г. отечественная статистика определяет индекс цен по формуле Ласпейреса, которой отдается предпочтение и в зарубежной статистике.
Основным назначением индекса цен является оценка динамики цен на товары производственного и непроизводственного потребления. В практике статистике используются два основных вида формул индекса цен. Это формулы Ласпейреса и Пааше.
) показывает, на сколько рублей изменилась стоимость продукции в результате изменения объема.
Индекс цен – это индекс качественного показателя. Индексируемой величиной будет цена товара, т.к. этот индекс характеризует изменение цен. Весом будет выступать количество произведенного товаров.
в числителе – фактическая стоимость продукции текущего периода, а в знаменателе – условная стоимость тех же товаров ценах базисного периода. Показывает, во сколько раз возросла (уменьшилась) стоимость продукции из-за изменения цен. Разность числителя и знаменателя – на сколько рублей изменилась стоимость продукции в результате роста (снижения) цен.
Стоимость продукции можно представить как произведение количества товара на его цену. Точно такая же связьсуществует и между индексами стоимости, физического объема и цен, т.е.
Разность числителя и знаменателя каждого индекса-сомножителя выражает размер изменения общей абсолютной величины под влиянием изменения одного фактора.
Все виды общих индексов в агрегатной форме представлены в табл. 10.1.
10.4. Средние индексы.
Средний индекс
При исчислении средних индексов используются две формы средних: арифметическая и гармоническая.
Арифметическая форма индекса используется сводных индексов количественных показателей, а гармоническая форма индекса – для расчета сводных индексов качественных показателей.
Например, средний арифметический индекс объема продукции вычисляется:
Средний гармонический индекс себестоимости можно исчислить так:
.
Индекс цен:
Индекс Доу-Джонса
Индекс Стэндарда и Пура (Standart and Poor's 500 Stock Index)
Система базисных и цепных индексов.
Индексы с постоянными и переменными весами.
Системой индексов
Система базисных индексов
Система цепных индексов
Система индексов стоимости имеет следующий вид:
· цепные индексы
· базисные индексы
Системой индексов с постоянными весами
Эти индексы строятся, как правило, для количественных показателей (например, индекс физического объема):
· базисные индексы
· цепные индексы
Система индексов с переменными весами
Поэтому эти индексы строятся, как правило, для качественных показателей (например, индекс цен):
· базисные индексы
· цепные индексы
Связь между цепными и базисными индексами
10.6. Индексы по составу явления
Изменение средней величины показателя зависит от двух факторов – изменения значения индексируемого показателя у отдельных единиц и изменения структуры явления.
Изменение структуры – это изменение доли отдельных групп единиц совокупности в общей их численности.
Индекс переменного состава – индекс, выражающий соотношение средних уровней изучаемого явления, относящихся в разным периодам времени. Например, индекс переменного состава стоимости продукции:
Отражает изменение не только изменение индексируемой величины (в данном случае, цены единицы продукции), но и структуры совокупности весов (объем).
Индекс постоянного состава – это индекс, исчисленный с весами, зафиксированными на уровне одного какого-либо периода, и показывающий изменение только индексируемой величины. Например, индекс фиксированного состава стоимости продукции:
Индекс структурных сдвигов – индекс, характеризующий влияние изменения структуры изучаемого явления на динамику среднего уровня этого явления:
Система взаимосвязанных индексов при анализе динамики средней цены имеет следующий вид:
10.7. Территориальные индексы
При построении территориальных индексов приходится решать вопрос, какие веса использовались при их исчислении. При сравнении цен двух стран (А и В) можно построить два индекса:
Формула Эджворта (индекс со стандартными весами):
10.8. Индексы Ласпейреса, Пааше и Фишера
В рыночном хозяйстве особое место уделяется индексу цен (оценка динамики цен, общий измеритель инфляции при макроэкономических исследованиях, установленных ставок налогов). До начала 90-х годов XX века отечественная статистика отдавала предпочтение индексу Пааше. Сложность его расчета заключается в том, что взвешивание по весам отчетного периода требует текущего сбора и обработки значительных объемов информации для формирования системы весов. Это связано с большими затратами различных видов ресурсов. Поэтому, начиная с 1991г. отечественная статистика определяет индекс цен по формуле Ласпейреса, которой отдается предпочтение и в зарубежной статистике.
Основным назначением индекса цен является оценка динамики цен на товары производственного и непроизводственного потребления. В практике статистике используются два основных вида формул индекса цен. Это формулы Ласпейреса и Пааше.