Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Наполнение (опорожнение) емкости

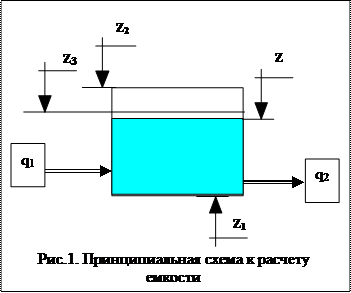Задана емкость постоянного сечения по глубине, площадью F. В нее подается вода с расходом q₁(м³/ч). В общем случае этот расход переменный во времени

q₁ = q₁(t). (1)

Функция q₁ может быть произвольной, в том числе, q₁= const.

Опорожнение емкости производится по второй трубе с расходом q₂, зависящим от уровня воды Z (м)

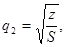(2)

где S – сопротивление отводных коммуникаций[1], ч²/м⁵.

Основное уравнение, описывающее динамику наполнения (опорожнения) – уравнение баланса

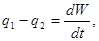(3)

где dW – изменение объема воды в бассейне за интервал времени dt.

При постоянной подаче и сечении бассейна (q₁, F= const)

dW =Fdz, (4)

откуда с учетом (2) получаем

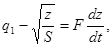(5)

Уравнение (5) решается при начальных условиях: t = 0, z = z_o. Решение уравнения (5) –

). (6)

Здесь следует отметить, что получить аналитическую зависимость Z(t) в явном виде не удастся (т.е именно Z(t), а не t(Z). как в (6)).

Поэтому придется использовать численные методы.

Результатами решения должны быть зависимости:

1. Уровня воды в емкости от времени.

2. Расхода из емкости от времени.

Методика численного решения задачи следующая:

1. Задаются исходные данные –

1.1. размеры емкости в плане А, В,

1.2. расход q₁,

1.3. сопротивление S,

1.4. отметки Zo, Z₁, Z₂, Z_3.

1.5. шаг счета Δ t.

2. На каждом шаге расчета определяют последовательно

· изменение уровня в емкости[2]

.

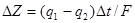· уровень воды-

Z_i+1=Z_i+Δ Z_i,

· расход воды из емкости по уравнению (2).

· если отметка уровня в бассейне становится больше Z₂, то подача воды прекращается ( q₁=0) до тех пор, пока уровень снизится до Z_{3 ,} после чего подача воды восстанавливается.

Для «продвинутых» студентов (в частности, для компьютерной специализации) можно предусмотреть такие возможности:

1. Изучение влияния шага счета Δ t на результаты.

2. Задание переменных значений F(Z) и q₁(t).

3. Сопоставление численного решения с точным – по уравнению (6).