Произвольной пространственной называется такая система сил, линии действия сил которой произвольно расположены в пространстве.

3.6.1. Условия равновесия произвольной пространственной системы сил

Векторная форма условия равновесия: для равновесия произвольной пространственной системы сил, приложенной к свободному абсолютно твердому телу, необходимо и достаточно, чтобы её главный вектор был равен нулю и главный момент системы сил относительно произвольной точки был равен нулю: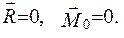

Аналитическая форма условия равновесия:

- для равновесия произвольной пространственной системы сил, приложенной к свободному абсолютно твердому телу, необходимо и достаточно, чтобы суммы проекций всех сил на каждую из трёх координатных осей были равны нулю, и суммы моментов всех сил системы относительно каждой из этих осей были равны нулю:

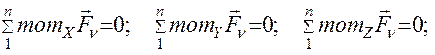
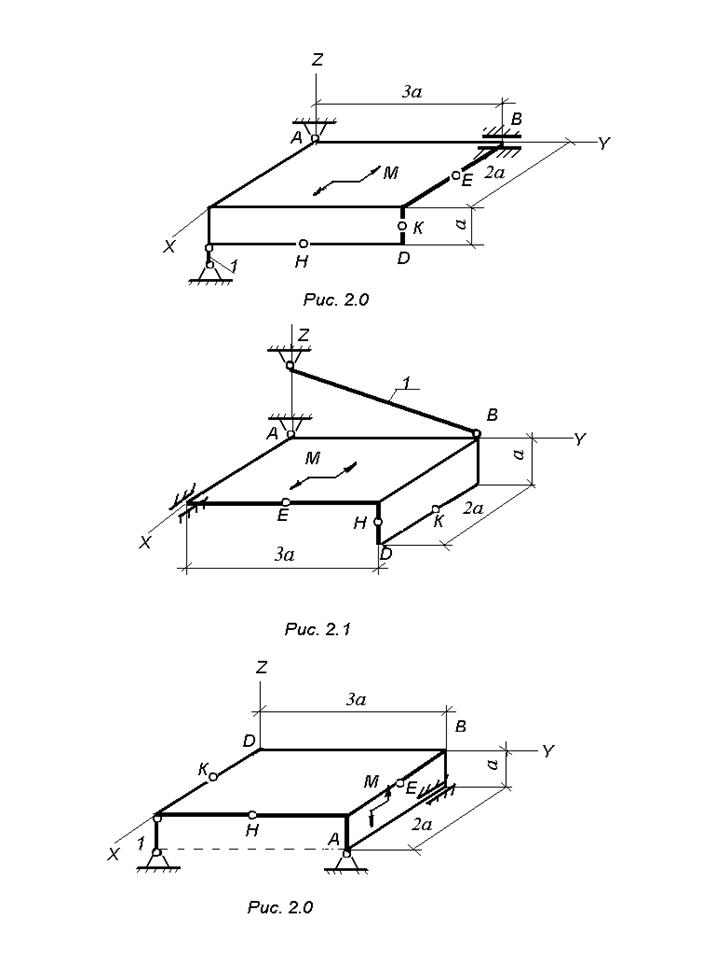
3.6.2. Дано: две однородные прямоугольные тонкие плиты жестко соединены (сварены) под прямым углом друг к другу и закреплены сферическим шарниром (или подпятником) в точке А, цилиндрическим шарниром (подшипником) в точке В и невесомым стержнем 1 (рис. С 2.0 – С 2.7) или же двумя подшипниками

в точках А и В и двумя невесомыми стержнями 1 и 2 (рис. С 2.8, С 2.9). Все стержни прикреплены к плитам и к неподвижным опорам шарнирами.

Размеры плит указаны на рисунках. Вес большей плиты Р₁=5 кН, вес меньшей плиты Р₁=3 кН. Каждая из плит расположена параллельно одной из плоскостей проекций (π ₁ - горизонтальной, π ₂ - фронтальной, π ₃ - профильной). При расчетах принять а=0, 6 м.

На плиты действуют пара сил с моментом М=4 кНм, лежащая в плоскости одной из плит, и две силы. Значения сил, их направления и точки приложения указаны в таблице С-2. Силы F₁ и F₄ лежат в плоскостях, параллельных плоскости π ₁; сила F₂ – в плоскости, параллельной плоскости π ₃; сила F₃ – в плоскости параллельной плоскости π ₂. Точки приложения сил (D, E, H, K) находятся в углах или серединах сторон плит.

Определить: реакции связей в точках А, В и реакцию стержня (стержней).

Указания. При решении задачи необходимо учесть, что реакция сферического шарнира (подпятника) имеет три составляющие (по трем координатным осям), а реакция цилиндрического шарнира (подшипника) – две составляющие, лежащие в плоскости, перпендикулярной оси шарнира. При вычислении момента силы её следует разложить на составляющие, параллельные координатным осям.

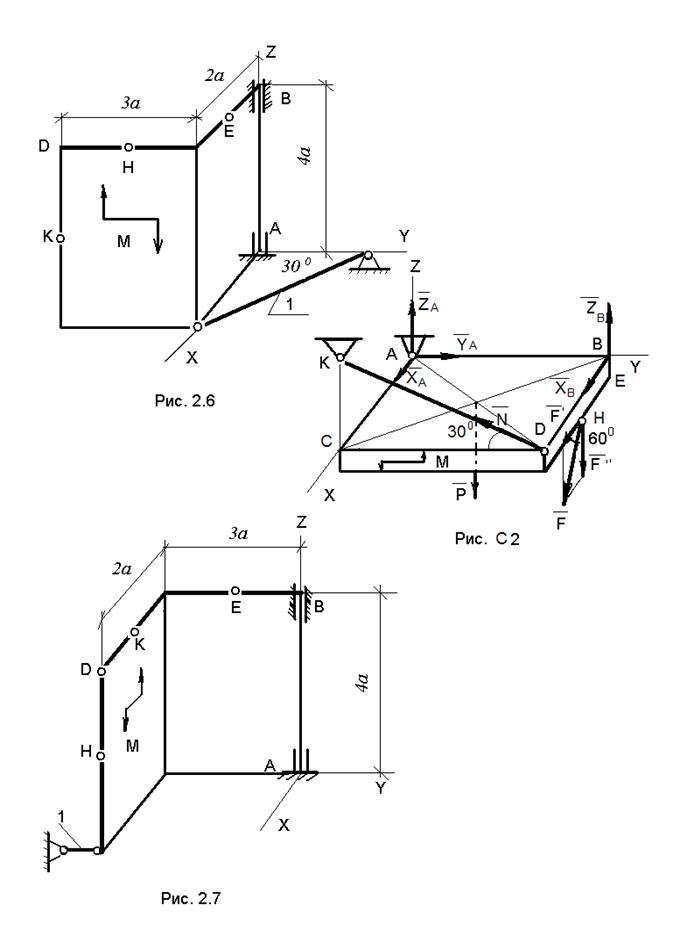
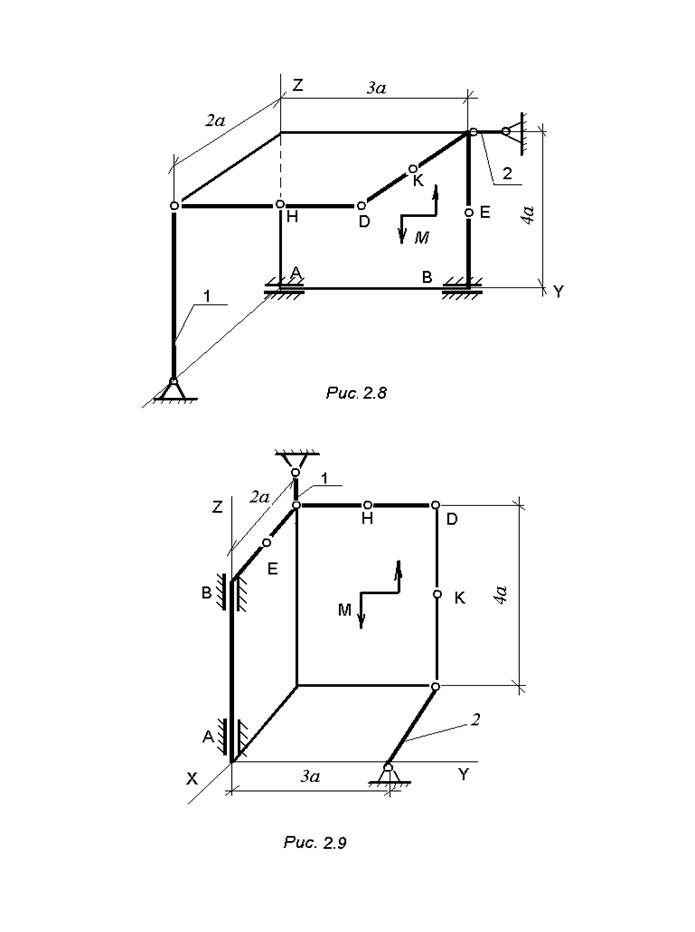
3.6.2. Пример С-2

Горизонтальная прямоугольная плита весом Р (рис. С-2) закреплена сферическим шарниром в точке А, цилиндрическим шарниром в точке В и невесомым стержнем DK. На плиту в плоскости, параллельной плоскости π ₃, действует сила F, а в плоскости, параллельной π ₂, – пара сил с моментом М.

Дано: Р = 3 кН; F = 8 кН; М= 4 кНм; α =60°; АС=0, 8 м; ВЕ=0, 4 м;

АВ=1, 2 м; ЕН=0, 4 м.

Определить: реакции в шарнирах А, В и стержне DK.

Решение

1. Рассмотрим равновесие плиты. На плиту действуют заданные силы P, F и пара сил с моментом М, а также реакции связей.

2. Систему координат выбираем таким образом, чтобы её начало совпадало с точкой А, а оси OX, OY были направлены по рёбрам плиты АС и АВ.

3. Реакцию сферического шарнира разложим на три составляющие , цилиндрического шарнира – на две составляющие 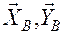, принадлежащие плоскости, перпендикулярной оси подшипника. Реакцию N стержня направляем вдоль стержня от D к K, предполагая, что он растянут.

4. Для определения шести неизвестных реакций составляем шесть уравнений равновесия пространственной системы сил, действующей на плиту (1-6):

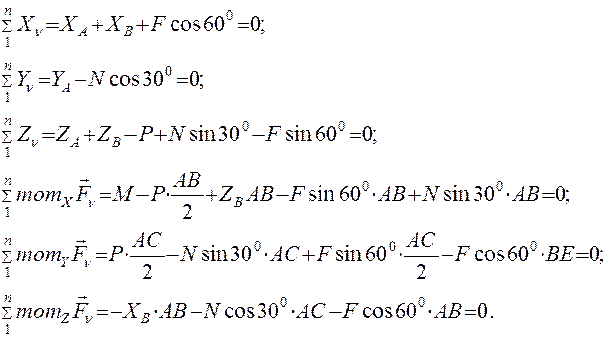
Для определения моментов силы относительно координатных осей разлагаем её на две составляющие , , 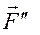параллельные осям OX, OY

(). Аналогично разложим по осям OY, OZ реакцию в стержне DK. Вычисляя моменты сил относительно координатных осей, следует помнить: момент силы относительно оси равен нулю, если линия действия силы пересекает ось или ей параллельна.

Подставив в полученные уравнения численные значения всех заданных величин и решив совместно эти уравнения, находим искомые реакции.

Ответ: X_A=3, 46 кН; Y_A= 5, 18 кН; Z_A= 4, 80 кН; X_В= -7, 46 кН; Z_В= 2, 15 кН; N=5, 96 кН.

Знак «-» указывает, что истинное направление составляющей силы реакции в точке В противоположно первоначально выбранному (рис. С -2).

Модуль реакции в шарнире А равен: , модуль реакции в шарнире В равен: .

Проверка: для проверки правильности решения необходимо составить условие равновесия для данной системы сил в новой системе координат.

Глава 4. КИНЕМАТИКА

4.1. Кинематика точки. Способы задания движения точки

Задать движение точки – значит указать способ, с помощью которого можно определить положение точки, её скорость и ускорение в любой момент времени относительно выбранной системы отсчёта.

Существуют три способа задания движения точки: векторный, координатный и естественный.

Векторный способ задания движения точки: выбирается система отсчета и задается радиус-вектор движущейся точки М как функция времени.

Эта функция должна быть непрерывной и дважды дифференцируемой по времени .

Траектория точки – это кривая линия, которую описывает точка (рис. 4. 1).

Скорость точки в данный момент времени равна пределу средней скорости при стремлении промежутка времени, в течение которого произошло перемещение, к нулю или первой производной радиуса-вектора точки по времени:

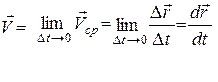или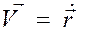

Рис. 4.1

Скорость точки всегда направлена по касательной к траектории её движения.

Ускорение точки в данный момент времени равно пределу среднего ускорения при стремлении промежутка времени, в течение которого произошло приращение скорости, к нулю или первой производной от скорости по времени или второй производной от радиуса-вектора точки по времени:

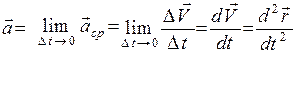или

Координатный способ задания движения точки: выбирается система отсчёта (рис. 4.2), задаются конечные уравнения движения точки, выражающие зависимость координат от времени: x=x(t), y=y(t), z=z(t) –

конечные уравнения движения точки являются параметрическими уравнениями её траектории.

Чтобы найти уравнение траектории точки в координатной форме, необходимо:

1. Исключить параметр t (время) из уравнения движения.

2. Найти область изменения координат, то есть определить, какие ограничения накладывают уравнения движения на движение точки по траектории.

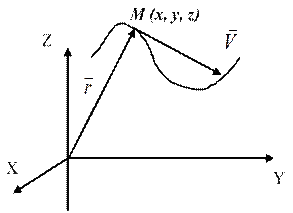
Рис. 4.2