
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!
Методика работы над алгоритмической задачей
|
|
Обозначения:
Комментарий: - сообщение для студента
Задание: - задание для ученика
Возможный диалог: сценарий диалога учителя и ученика
Основные этапы работы учителя
Комментарий:
Внести в таблицу комментарий, поясняющий деятельность учителя при работе над алгоритмической задачей.
| № | Примечания для учителя | |
| 1. | Поиск задачи. При необходимости корректировка условия задачи | Подбирает задачу в зависимости от целей урока |
| 2. | Непосредственное решение задачи | Решает задачу одним из возможных способов |
| 3. | Осмысление различных вариантов решения. Выбор варианта, предъявляемого учащимся. | При помощи исполнителя/без помощи исполнителя Разные варианты решения |
| 4. | Выявление базы знаний, необходимой для решения задачи. | Какие алгоритмические конструкции используются; СКИ; Математический аппарат |
| 5. | Выбор варианта актуализации знаний учащихся для решения задачи | Опрос, беседа, краткий обзор что еще? |
| 6. | Выделение основных модулей (метод последовательного уточнения) в процессе решения задачи | Что за чем следует С чего надо начать Что дальше Чем закончить |
| 7. | Разработка сценария решения задачи | Запись последовательности решения задачи с комментариями |
| 8. | Выделение основных затруднений учащихся в процессе решения задачи | Определяет места в сценарии, которые могут вызвать затруднение учащихся |
| 9. | Выбор способа оформления решения задачи | Выбирает способ оформления задачи в зависимости от цели урока |
| 10. | Разработка системы вопросов учащимся в процессе решения задачи | Записывает уточняющие, ориентирующие вопросы по ходу сценария решения задачи |
| 11. | Разработка способов организации деятельности учащихся по проверке правильности разработанных алгоритмов (отладка вспомогательных модулей и фрагментов программ, тестирование и отладка основного алгоритма) | Выбирает метод проверки правильности выполнения алгоритмов: совместная работа у доски, работа с исполнителем, взаимопроверка, другое |
| 12. | Разработка способов организации самостоятельной деятельности учащихся по завершению решения, закреплению полученных знаний и умений | Самостоятельное выполнение заданий по предложенному образцу, Выполнение заданий с проверкой у доски; Другое |
Комментарий: Рассмотрим основные этапы работы учителя на конкретном примере.
Методика работы над алгоритмической задачей
Комментарий:
В своих методических статьях и выступлениях А. П. Ершов выдвигал следующую идею применительно к школьной информатике: различать исполнителей алгоритмов, работающих с величинами и работающих «в обстановке»; а соответствующие алгоритмы для этих исполнителей называть алгоритмами работы с величинами и алгоритмами работы «в обстановке». В алгоритмах второго типа отсутствуют такие элементы, как величины (переменные, константы), команда присваивания, однако используются все типы алгоритмических структур. Идея применения таких исполнителей для обучения в полной мере была реализована в более поздних учебных изданиях.
Методика обучения алгоритмизации на учебных исполнителях, работающих «в обстановке»
Задача 1.
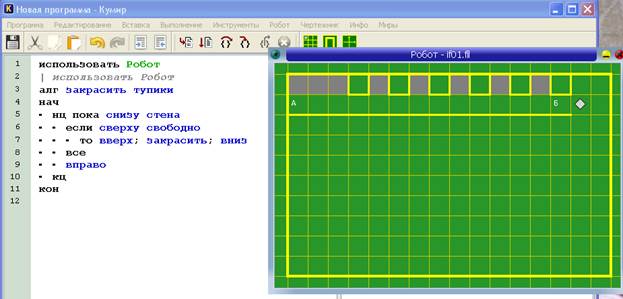
Робот стоит в левой клетке горизонтального коридора, от которого вверх отходят тупики размером в одну клетку. Требуется провести Робота из коридора вправо (из клетки А в клетку Б), а тупики закрасить.
Задание
Робот стоит в левой клетке горизонтального коридора, от которого вверх отходят тупики размером в одну клетку. Требуется провести Робота из коридора вправо (из клетки А в клетку Б), а тупики закрасить
Учитель: Что необходимо вспомнить, чтобы решить задачу?
Комментарий:
Показывается методическое пособие, где перечислены СКИ «Робот».
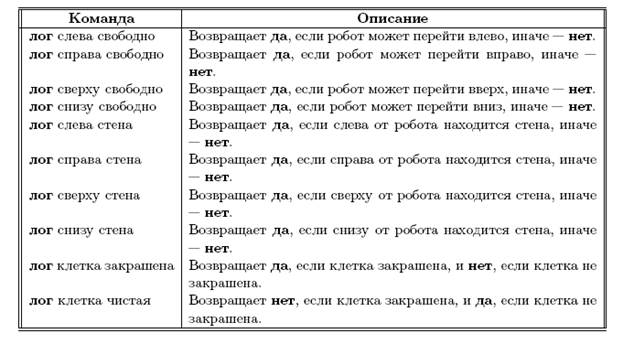
Команды-действия

Команды-проверки
Возможный диалог:
| Деятельность педагога | Деятельность ученика | Состояние доски |
| Рассмотрение классной задачи. Учитель читает задачу на странице 108. | - Дети слушают и читают условие задачи в учебнике | |
| – Что мы знаем из условия задачи? | - Дан горизонтальный коридор. - От этого коридора вверх отходят тупики размером в одну клетку. - Требуется вывести Робота из коридора вправо. -Тупики следует закрасить | 
|
| - Что нужно выполнить, чтобы ответить на вопрос задачи? | - Нужно пойти вправо до конца коридора. При этом, если будут встречаться тупики, их нужно будет закрасить. | нач нцпока снизу стена если сверху свободно то вверх закрасить вниз все вправо кц кон |
| Теперь разобьем задачу на подзадачи, распишем по пунктам. | ||
| - Каков наш первый шаг? | - Идем вправо до появления первого тупика | |
| - Как долго мы будем идти? | - неизвестно | |
| То есть Робот будет идти до тех пор, пока не дойдет до тупика. | ||
| - Какой цикл здесь лучше использовать? | - Пока | |
| - Правильно. Нам уже известно, что цикл пока – цикл с условием. Какое условие будет на первом шаге? | - Пока снизу стена идем вправо. | |
| - Правильно. А снизу стена – это логическая команда? | - Да | |
| Выберем из предложенных логических команд ту, которая подойдет для выполнения первого шага. Оформим первый шаг решения задачи на алгоритмическом языке. | - Это команда «снизу стена». - Выходит ученик и оформляет цикл для 1 шага | |
| - Какой следующий шаг нам нужно выполнить? | - Нужно проследить, когда Робот дойдет до первого тупика. | |
| - Что для этого нужно сделать? | - Нужно поставить условие если.. | |
| - Какая команда в условии если нам понадобится? | - Сверху свободно | |
| Это логическая команда? - | - Да. | |
| - Что должен выполнить Робот, если сверху будет свободно? | - Он должен подняться вверх, | |
| Что на следующем шаге должен выполнить Робот в этом тупике? | - закрасить тупик | |
| - Какую команду при этом нужно использовать? | закрасить | |
| - Каков следующий шаг? | - Робот должен опуститься вниз. | |
| - Какую команду будем использовать? - Вышли ли мы из тупика? | - Команда вниз. | |
| - Какое действие мы должны выполнить далее? | - Робот должен пойти вправо. | |
| - Правильно! Следовательно, команда если закончилась. Какое действие далее должен выполнить Робот? | - Роботу нужно двигаться вправо. | |
| - До каких пор Робот будет двигаться вправо? | - Пока опять не появится вверху тупик | |
| - Т.е. нам необходимо условие если поставить внутри цикла пока. | ||
| Чего мы этим добьемся? | - Робот будет идти по коридору к выходу, заходить во все тупики и закрашивать их | |
| - До каких пор Робот будет двигаться по коридору? | - Пока снизу стена. | |
| - Решили мы задачу? | Да | |
| - Теперь садимся за компьютеры и попробуем написать эту задачу в программе. Проверим правильность нашего решения. | - Теперь садимся за компьютеры и попробуем написать эту задачу в программе. Проверим правильность нашего решения. |
Комментарий: Какой метод использовал учитель?
Методика решения алгоритмической задачи с величинами
Основные типы учебных алгоритмических задач.
Комментарий:
Для закрепления основных понятий, связанных с определением алгоритма, полезно рассмотреть с учениками несколько заданий следующего содержания:
1. Выполнить роль исполнителя: дан алгоритм, формально исполнить его;
2. Определить исполнителя и систему команд для данного вида работы;
3. В рамках данной системы команд построить алгоритм;
4. Определить необходимый набор исходных данных для решения задачи.
В качестве примера задачи первого типа можно использовать алгоритм игры Баше, рассматриваемый в учебниках [1, стр. 60 № 8а)].
В книгах правила игры определены так: В игре используются 11, 16, 21, 26,... предметов. За один ход можно брать от 1 до 4 предметов. Проигрывает тот игрок, который берет последний предмет.
Рассматривается алгоритм, благодаря которому всегда выигрывает игрок, берущий предметы вторым.
Задача 2.
«Разгадать загадку» алгоритма, т.е. объяснить, почему второй игрок всегда выигрывает?
Задача 3.
Составить алгоритм, по которому игрок, делающий ход вторым, может выиграть в том случае, если не ошибается.
Возможный диалог:
| Деятельность педагога | Деятельность ученика | Состояние доски |
| - Почему игрок, начинающий вторым всегда выигрывает? | Существует выигрышная тактика, которая позволяет выигрывать | |
| - Давайте выявим «выигрышную» тактику? | ||
| - Что дано в задаче? | 16 предметов | Дано 16 предметов |
| - Что нам еще известно в задаче? | Игроки по очереди вводят число от 1 до 4 | n от 1 до 4 А: ввод числа от 1 до 4 В: ввод числа от 1 до 4 |
| _ Что нам надо получить в итоге? | - Проигрывает тот, кто берет последний предмет. | Остался 1 предмет. В: ввод числа 1 Игра закончена. |
| - Как мы достигнем того, чтобы второй игрок сделал ход последним? - «выигрышный» алгоритм игры Баше можно получить, если рассуждать «с конца игры», то есть рассмотреть сначала позицию перед последним ходом | - надо чтобы перед последним ходом второго игрока остался 1 предмет предмета | Если осталось N = 1 предметов, то В: взять n предметов (N =1) |
| - Сколько предметов должно остаться на предпоследнем ходу второго игрока? | - Для выигрыша надо оставить противнику перед его последним ходом n + 1 предмет. Тогда, сколько бы он ни взял (больше n брать нельзя), своим ходом вы забираете последний предмет. | Зарисовать предметы N + 1 2(N + 1) 3 (N + 1) |
| - Что можно сказать о действиях игроков | - они повторяются | |
| - До каких пор будут повторяться действия? | Пока не останется один предмет | Пока N > 1 |
| - Какую команду мы можем использовать? | пока | нц пока кц |
| Как мы узнаем, что игра закончилась? | Останется один предмет | |
| Какую команду мы можем применить, чтобы сообщить о количестве оставшихся предметах? | вывод | Вывод N |
Задание
Давайте составим алгоритм в виде блок схемы.
Возможный диалог:
Учитель: Что необходимо вспомнить, чтобы решить задачу?
Ученик: Описание величин: типы, виды величин; команда присваивания; команды алгоритмического языка: нц-пока-кц.
Учитель: Какие величины мы используем в данном алгоритме?
Ученик: Общее количество предметов; количество предметов, которые берет первый игрок за один ход; количество предметов, которые берет компьютер за один ход.
Учитель: Определите имя, тип и значение этих величин
Ученики:
N – общее количество предметов; вещ, N = 16.
b – количество предметов, которые берет первый игрок за один ход; вещ, b от 1 до 4.
a – количество предметов, которые берет компьютер за один ход; вещ, a от 1 до 4.
Учитель: Запишите последовательность действий, которые выполняют игроки.
Ученики:
И – игрок
К – компьютер
Комментарий: Заполнить таблицу.
| Этапы | команды | состояние |
| К: задает 16 предметов | N: =16 | N: =16 |
| И: берет b предметов | b: =n | |
| К: берет (5 – n) предметов | a: =5 – n | |
| К: количество предметов уменьшается на 5 | N: =N – 5 | N: =11 |
| И: берет b предметов | b: =n | |
| К: берет (5 – n) предметов | a: =5 – n | |
| К: количество предметов уменьшается на 5 | N: =N – 5 | N: =6 |
| И: берет b предметов | b: =n | |
| К: берет (5 – n) предметов | a: =5 – n | |
| К: количество предметов уменьшается на 5 | N: =N – 5 | N: =1 |
| И: берет 1 предмет. Конец игре | b: =n | N: =0 |
Учитель: Какой цикл можно использовать для упрощения записи алгоритма
Ученик: Цикл пока
Задание
Учитель: Составьте алгоритм в виде блок-схемы используя «цикл пока»
Ученики:

        
 
| Состояние доски | ||||||||||
| нач | |||||||||||
| цел a, цел b, цел N | |||||||||||
| N: =16 | |||||||||||
| нц пока N: > 1 | |||||||||||
| Ввод b | |||||||||||
| a: =5-в | |||||||||||
| N: = N-5 | |||||||||||
| кц | |||||||||||
| вывод N=1 | |||||||||||
| кон | |||||||||||
Задание
Запишите программу на языке КуМир, используя текст на строке вывода для организации диалога между игроком и компьютером
Возможный диалог:
Учитель: Какие величины мы используем?
Ученики: Количество предметов; количество предметов, которые берет первый игрок за один ход; количество предметов, которые берет компьютер за один ход
Учитель: Какие величины являются постоянными, а какие переменные?
Ученики: Все величины переменные - количество предметов; количество предметов, которые берет первый игрок за один ход; количество предметов, которые берет компьютер за один ход.
Учитель: Какие команды мы используем в данной программе?
Ученики: команды ввода/вывода; присваивания; цикл пока
Учитель: Запишите программу на языке КуМир, используя текст на строке вывода для организации диалога между игроком и компьютером
| алг нач цел a, b, N N: =16 вывод “Задано 16 предметов” нц пока N: > 1 вывод “Ваш ход. Можете взять от 1 до 4 предметов” ввод b N: = N-5 a: =5-b вывод “Я беру ”; вывод a; вывод “предметов” вывод “Осталось ”; вывод n; вывод“ предметов” кц вывод“Остался один предмет. Ваш ход” кон | Начало алгоритма |
| Имя и тип величин | |
| Операция присвоения | |
| Сообщение о начале игры | |
| Условие; операция будет повторяться, пока количество предметов больше N: =1. | |
| Сообщение для игрока с указание правил игры | |
| Игрок вводит число, равное количеству выбранных предметов | |
| Операция присваивания | |
| Операция присваивания | |
| Сообщение компьютера о своих действиях | |
| Сообщение компьютера о состоянии игры | |
| Сообщение о окончании игры | |
Учитель: Проверяем правильность составленной программы, работая в среде КуМир
Ученики:
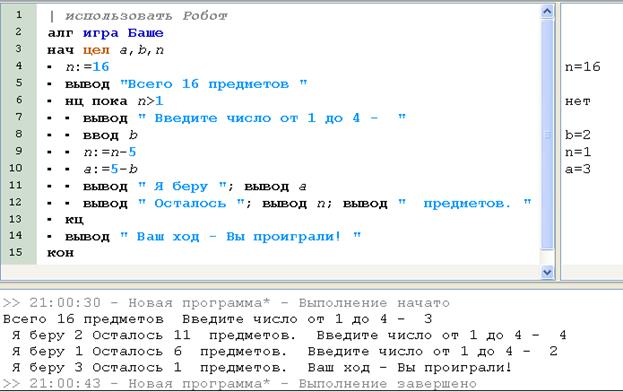
Учитель: Домашнее задание
Комментарий:
Можно предложить учащимся несколько заданий аналитического характера на тему игры Баше.
В качестве примера задачи первого типа можно использовать алгоритм игры Баше, рассматриваемый в учебниках. В книгах правила игры определены так: в игре используются 7, 11, 15, 19 предметов. За один ход можно брать 1, 2 или 3 предмета. Проигрывает тот игрок, который берет последний предмет. Предлагается алгоритм выигрыша для первого игрока.
Задача 4.
Попробуйте провести математический анализ игры Баше в общем случае для N камней. Определите правила игры (т. е. сколько камней можно брать за один ход), при котором имеется выигрышный алгоритм. Опишите этот алгоритм в виде последовательности команд.
Решение. Выигрышный алгоритм для второго игрока можно построить только в тех случаях, когда исходное число камней (N) представимо в виде: N = Х × K+ 1, где Х и К— натуральные числа. По правилам игры за один ход можно брать от 1 до X— 1 камней. Второй игрок будет всегда выигрывать, если своим ходом он будет дополнять число камней, взятых соперником, до X. Например, пусть N= 25. Это значение можно представить: 25 = 4× 6 + 1. Следовательно, правило игры должно быть таким: за один ход можно брать 1— 2— 3 камня. А для того, чтобы второй игрок всегда выигрывал, в свой ход он должен дополнять ход соперника до 4 камней.
|
|
