
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Алгоритмы оптимального когерентного приема для правила максимальной апостериорной вероятности
|
|
Для пояснения алгоритма предположим, что все искажения в канале строго детерминированы и случайным является только гауссовский аддитивный шум n (t), который вначале полагаем белым, со спектральной плотностью N 0. Это значит, что при передаче символа bi (i = 0, 1,..., т- 1) принимаемое колебание можно описать моделью (4.48):
z (t) = si (t) +n (t), 0£ t £ T, (1)
где все si (t)= gf (t - t - kT),  = gui (t - t) известны. Не известна лишь реализация помехи и позиция (индекс i) действительно переданного сигнала, который и должна определить решающая схема.
= gui (t - t) известны. Не известна лишь реализация помехи и позиция (индекс i) действительно переданного сигнала, который и должна определить решающая схема.
Будем также считать, что все si, являются финитными сигналами, длительность которых Т. Это имеет место, если передаваемые сигналы ui (t)финитны и имеют одинаковую длительность.
В дальнейшем будем везде полагать, что в системе обеспечена надёжная тактовая синхронизация, т.е. границы тактового интервала, на котором приходит сигнал si (t), известны точно. Момент начала посылки si (t) примем за нуль.
Пусть источник сигнала посылает разовый символ br с вероятностью p (br). Эта вероятность определяется свойствами источника (а также зависит от ранее посылаемых символов). Поэтому  .
.
Символ br преобразуется в сигнал sr (t), на который действуют аддитивные помехи, в результате чего на вход приемника поступает случайный процесс z (t). Распределение вероятностей можно определить, например, на k -х сечениях в отрезке времени 0£ t £ T.
Пусть wk (z ½ br) – k -мерная условная плотность распределения отсчетов функции z (t) в точках ti (i =1, 2, …, k; 0£ t £ T). Эта плотность распределения вероятности определяется реализацией сигнала и помехами в канале. Если бы не было помех, то функция z (t) совпадала бы с sr (t)= msi (t - t), (где m и t - считаются известными, т.к. рассматриваем когерентный прием) и при заданном символе br была бы не случайной. Отличие z (t) и sr (t) вызвано только помехами.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Безусловная k -мерная плотность распределения отсчетов функции z (t) определяется по формуле полной вероятности:
wk (z)= 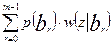 . (2)
. (2)
Найдем условную вероятность p (br ½ z) того, что поступившим на вход канала символом является br, при условии, что на выходе канала имеется функция z (t) (заданная отсчетами времени t 1, …, tk).
p (br ½ z)= 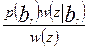 . (3)
. (3)
Формула Байеса (3) определяет значения вероятности, которые называются апостериорными, т.е. полученные после опыта (после приема функции z (t) вероятностями символов br) в отличие от априорных (т.е. существовавших до опыта) или безусловных вероятностей p (br).
Решающая схема, на вход которой поступил сигнал z (t) может принять одно из m решений, которое обозначим через bi (i =1, …, m). Решение bl - означает, что переданным символом считается bl. Если в результате обработки сигнала z (t) принято решение bl, то это решение верно, если переданным символом, вызвавшим функцию z (t) являлся bl, то вероятность его равна p (br ½ z). Вероятность ошибки p (ош ½ z, bl) при выборе решения bl определяется:
p (ош ½ z, bl)=1- p (bl ½ z) (4)
Сравним между собой две решающие схемы, из которых одна в результате обработки сигнала z (t) выбирает решение bi, а другая при том же z (t) выбирает - bj. Из выражения (4) следует, что p (ош ½ z, bi)< p (ош ½ z, bj) если p (bi ½ z)> p (bj ½ z), то есть вероятность ошибки меньше у той решающей схемы, которая выбирает решение, соответствующее большей апостериорной вероятности.
Таким образом, решающая схема, которая при всяком поступающим на вход демодулятора сигнала z (t) выбирает решение bl, соответствующее максимальному значению апостериорной вероятности p (bl ½ z)= 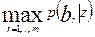 обеспечивает меньшую вероятность ошибок, чем всякая другая решающая схема.
обеспечивает меньшую вероятность ошибок, чем всякая другая решающая схема.
Таким образом, оптимальное правило (соответствующее критерию идеального наблюдателя) можно сформулировать следующим образом: при поступлении сигнала z (t) решающая схема выбирает решение bl, если апостериорная вероятность символа bl больше, чем вероятности всех остальных символов:
p (bl ½ z)> p (br ½ z) (r =1, …, m; r ¹ l) (5)
Выражение (5) – сокращенная запись системы из (m -1) неравенств, соответствующих различным значениям r. Решение принимается тогда, когда все эти неравенства выполнены.
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
|
|
