💸 Как сделать бизнес проще, а карман толще?

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое раписание, но и напоминать клиентам о визитах тоже. Проблема в том, что средняя цена по рынку за такой сервис — 800 руб/мес или почти 15 000 руб за год. И это минимальный функционал. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!

Развилка. Достаточно часто то или иное действие должно быть выполнено в зависимости от значения логического выражения

Достаточно часто то или иное действие должно быть выполнено в зависимости от значения логического выражения, выступающего в качестве условия. В таких случаях используется развилка.

Пример 1. Вычислить значение функции

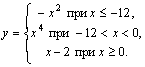
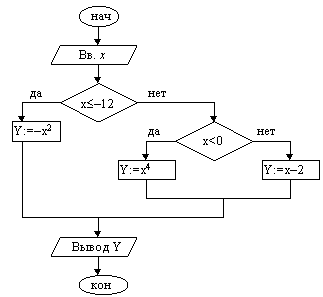
1. Ввести x. 2. Если x£ –12, то y: =–x2 3. Если x< 0, то y: =x4 4. y: = x–2 5. Вывести y 6. Конец

При тестировании алгоритмов с развилкой необходимо подбирать такие исходные данные, чтобы можно было проверить все ветви. В приведенном выше примере должно быть по крайней мере три тестовых набора.

Пример 2. Дано натуральное число n. Если число нечётное и его удвоение не приведет к выходу за 32767 (двухбайтовое целое число со знаком), удвоить его, иначе — оставить без изменения.

Чтобы удовлетворить условию удвоения, число n должно быть нечетным и меньше 16384.

1. Ввести число n 2. Если число n нечетное и меньше 16384, то n: = n * 2 3. Вывод n 4. Конец

Рассмотренный пример иллюстрирует неполную развилку. Также следует отметить, здесь логическое выражение, являющееся условием, содержит 2 операнда.

Циклы

Если какие-либо операторы необходимо выполнить несколько раз, то их не переписывают каждый раз заново, а организуют цикл.

Пример 1. Подсчитать количество нечетных цифр в записи натурального числа n.

Идея решения. Из заданного числа выбирать из младшего разряда цифру за цифрой до тех пор, пока оно не исчерпается, т.е. станет равным нулю. Каждую нечётную цифру учитывать.

1. Ввести число n 2. K: = 0 {подготавливаем счётчик} 3. Если n = 0, переход к п. 7 4. Если n mod 10 mod 2 = 1, то K: = K +1 5. n: = n div 10 6. Переход к п. 3 7. Вывод K 8. Конец

Задача решена двумя способами. Слева решение оформлено с использованием цикла с предусловием, справа — с постусловием.

Пример 2. Дана последовательность, общий член которой определяется формулой

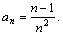
Вычислить при n > 2 сумму тех ее членов, которые больше заданного числа e.

При решении задачи находится очередной член последовательно и, если он больше e, добавляется к сумме.

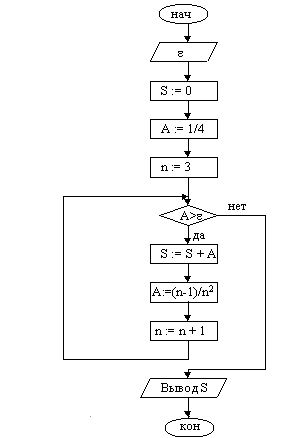
1. Ввести e 2. S: = 0 3. A: = 1/4 4. n: = 3 5. Сравнить А с e. Если A> =e, переход к п. 10 6. S: = S + A 7. A: = (n-1)/(n*n) 8. n: = n + 1 9. Переход к п. 5 10. Вывод S 11. Конец

В рассмотренных выше примерах количество повторений заранее неизвестно. В первом оно зависит от количества цифр в записи натурального числа, во втором — от числа e.

В тех же случая, когда количество шагов известно из условия задачи, проще и предпочтительней использовать цикл с параметром.

Пример 3. Найти произведение первых k натуральных чисел, кратных трём.

При составлении алгоритма учтем, что первое натуральное число, кратное 3, есть тройка, а все последующие больше предыдущего на 3.

1. Ввод k 2. P: = 1 {здесь накапливаем произведение} 3. T: = 0 {здесь будут числа, кратные 3} 4. I: = 1 5. Если I > k, переход к п. 10 6. T: = T + 3 7. P: = P * T 8. I: = I + 1 9. Перейти к п. 5 10. Вывод P 11. Конец

Другие примеры будут записаны уже на ЯПВУ. В настоящей же публикации предпринята попытка продемонстрировать, что изучение программирования разумно начинать собственно с разработки алгоритмов, не акцентируя первоначально внимания на записи алгоритма на том или ином языке программирования. В то же время автор, являясь сторонником структурного подхода к программированию, предлагает придерживаться этого подхода и при программировании на уровне блок-схем.