💸 Как сделать бизнес проще, а карман толще?

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое раписание, но и напоминать клиентам о визитах тоже. Проблема в том, что средняя цена по рынку за такой сервис — 800 руб/мес или почти 15 000 руб за год. И это минимальный функционал. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!

Резонансный и гетеродинный методы измерения частоты

Принцип действия резонансного метода основан на сравнении измеряемой частоты ƒ _х с собственной резонансной частотой ƒ _р градуированного колебательного контура или резонатора. Измерительные приборы, работающие на основе этого метода, называются резонансными частотомерами; их обобщенная структурная схема приведена на рисунке.

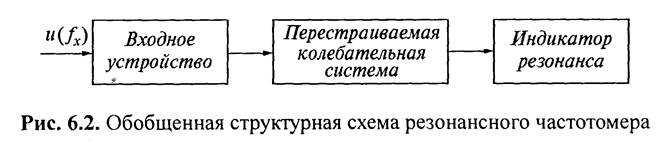Перестраиваемая колебательная система через входное устройство возбуждается сигналом источника измеряемой частоты и( ƒ _х). Интенсивность колебаний в колебательной системе резко увеличивается в момент резонанса, т.е. при ƒ _х = ƒ _р. Данный момент фиксируется индикатором резонанса, связанного с колебательной системой, и значение измеряемой частоты ƒ _х; считывается с градуированной шкалы механизма настройки. В качестве колебательной системы на частотах до сотен мегагерц используют колебательные контуры; на частотах до 1 ГГц — контуры с распределенными параметрами (отрезки коаксиальной линии); на частотах свыше 1 ГГц — объемные резонаторы.

На рис. 6.3 приведена упрощенная структурная схема резонансного частотомера (на СВЧ его называют волномером) с объемным резонатором.

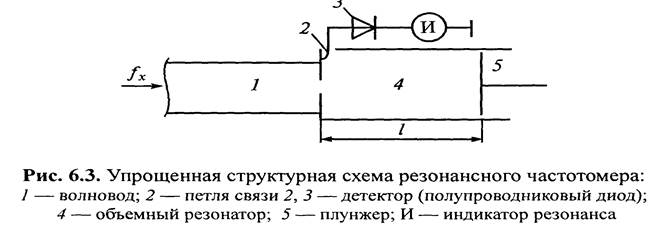Линейный размер резонатора l в момент настройки в резонанс однозначно связан с длиной волны λ возбуждаемых в нем электромагнитных колебаний. Резонанс наступает при длине резонатора l = п λ /2, где n = 1, 2, 3 и т.д. Поэтому, перемещая плунжер 5 до момента получения первого резонанса, а затем следующего и оценивая по отсчетной шкале разность Δ l = l₁ - l ₂ = λ /2, можно определить длину волны λ, где l₁ и l ₂ — показания отсчетной шкалы в момент 1- и 2-го резонансов. Измеренную частоту ƒ _х вычисляют по формуле ƒ _х = с/ λ, где с — скорость распространения света в вакууме. Чтобы увеличить точность измерений частоты, необходимо повышать добротность Q резонаторов. Для этого их внутренние поверхности полируют и серебрят, доводя величину Q до значения (5-10)10³.

Резонансные частотомеры имеют сравнительно простое устройство и достаточно удобны в эксплуатации. Наиболее точные из таких приборов обеспечивают измерение частоты с относительной погрешностью 10^-3 - 10^-4 Основными источниками погрешностей измерения частоты являются погрешность настройки в резонанс резонатора, погрешность отсчетной шкалы и погрешность считывания данных.

Гетеродинный метод является одной из разновидностей методов сравнения измеряемой частоты ƒ _х с частотой эталонного генератора — гетеродина. Этот метод использует принцип построения измерительных схем с нулевыми биениями. Упрощенная структурная схема гетеродинного частотомера представлена на рис. 6.4.

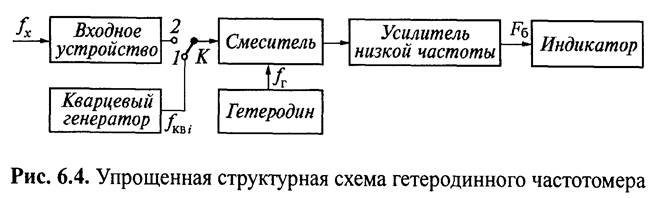Она содержит: входное устройство, кварцевый генератор, смеситель, гетеродин, усилитель низкой частоты и индикатор (нулевых биений). Действие гетеродинного частотомера сводится к простому принципу: при переводе ключа К в; положение 1 производят калибровку шкалы гетеродина; при положении 2 — измерение частоты ƒ _х, подаваемой на входное устройство.

Калибровку шкалы гетеродина осуществляют непосредственно перед измерением с помощью дополнительного, кварцевого генератора. Сигнал, поступающий с, генератора, имеет сложную форму и содержит ряд гармонических составляющих с кратными частотами:

ƒ _{кв 1,} ƒ _{кв 2},..., ƒ _{кв i},..., ƒ _{кв n} где п — номер гармоники. Эти частоты называют кварцевыми точками. Отсчетный лимб гетеродина устанавливают в положение, соответствующее ближайшей к измеряемой частоте ƒ _x; кварцевой точке (примерное значение измеряемой частоты должно быть известно, иначе процесс измерения очень усложняется). Сигналы с кварцевого генератора ƒ _{кв i;} и гетеродина ƒ _г поступают на смеситель, поэтому на его выходе возникают колебания с суммарными, разностными и комбинационными частотами. Индикатор фиксирует наличие сигнала биений на минимальной разностной частоте F₆ = |ƒ _{кв i} - ƒ _г|, проходящего через усилитель низкой частоты (высокочастотные составляющие, получающиеся в результате смешения частот кварцевого генератора и гетеродина, через усилитель низкой частоты не проходят). Меняя емкость в контуре гетеродина, получают нулевые биения, следовательно, частота гетеродина становится равной частоте кварцевой гармоники ƒ _г ≈ ƒ _{кв i}.

Затем приступают к измерению неизвестной частоты ƒ _x, переводя ключ К в положение 2. Вращая отсчетный лимб гетеродина, добиваются нулевых биений и по откорректированной шкале гетеродина определяют значение ƒ _х ≈ ƒ _г.

Гетеродинные частотомеры являются достаточно точными измерительными приборами. Их относительная погрешность измерения лежит в пределах 10^-3...10^-5. Однако в диапазоне средних частот (до 300 МГц и ниже) их вытесняют электронно-счетные частотомеры, которые обеспечивают ту же высокую точность, но значительно проще в эксплуатации.

В диапазоне СВЧ-колебаний гетеродинный метод измерения частоты применяется совместно с цифровыми методами. Расширение предела измерения до 10... 12 ГГц достигается за счет переноса (преобразования) измеряемой частоты в область более низких частот. Такой перенос можно осуществить, например, с помощью дискретного гетеродинного преобразователя частоты, структурная схема которого вместе с цифровым частотомером приведена на рис. 6.5.

В состав цифрового частотомера входит генератор опорной (образцовой) частоты ƒ _о,. Эта частота поступает на нелинейный элемент (генератор гармоник), который формирует сетку гармонических составляющих ƒ _n = п ƒ ₀, где п = 1, 2,...— целые числа. С помощью перестраиваемого фильтра (объемный резонатор с отсчетной шкалой) добиваются выделения из них гармоники ƒ _n, ближайшей к измеряемой частоте ƒ _х. При этом на выходе смесителя появляется сигнал с разностной частотой Δ ƒ = |ƒ _х - nf₀ |. Усилитель промежуточной частоты УПЧ имеет полосу пропускания, соизмеримую с разностной частотой Δ ƒ.

Результат измерения неизвестной частоты f_x колебаний вычисляют по формуле f_x= nf_o± Δ ƒ, в которой номер гармоники п считывается со шкалы перестраиваемого фильтра. Поскольку последнее выражение неоднозначно, то для получения наиболее точного результата проводят второе измерение, выбирая с помощью перестраиваемого фильтра гармонику (п ± 1) ƒ ₀, соседнюю с гармоникой nf₀. Если результаты вычисления частоты ƒ _х совпали при двух измерениях, то они считаются верными.

Электрическая схема электродинамического частотомера на основе логометрического механизма и векторная диаграмма токов приведены на рис. 13.10.

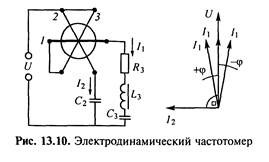Рамки подвижной части частотомера скреплены между собой под углом 90°. Параметры контура L₃, С₃ и R₃ подобраны таким образом, что частота резонанса напряжений близка к средней частоте диапазона измерения ƒ _ср = (ƒ _н +ƒ _к)/2, гдеƒ _н и ƒ _к — соответственно начальное и конечное значения шкалы прибора.

Вращающие моменты, действующие на подвижную часть, равны:

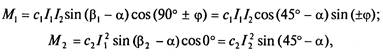где β ₁ = 135°, β ₂ = 45° — соответственно углы между плоскостями первой и второй рамок и плоскостью неподвижной катушки при α = 0.

Момент М₁, зависит от угла поворота подвижной части α и фазового сдвига между токами I₁ и I₂, который, в свою очередь, зависит от измеряемой частоты f_x. Момент М₂ зависит только от угла α и не зависит от частоты f_x. Моменты M₁ и М₂ действуют навстречу друг другу, и подвижная часть поворачивается до тех пор, пока не наступает равенство М₁ = М₂. Токи I₁ и I₂ с изменением измеряемой частоты изменяются незначительно, и поэтому из равенства моментов следует:

tg(45^o – α) = c sin(±φ) .