Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
-
Как продвинуть сайт на первые места?Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.Ускорение продвиженияЕсли вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги. Начать продвижение сайта
-
Сервис онлайн-записи на собственном Telegram-ботеТот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно. Чат-бот для мастеров и специалистов, который упрощает ведение записей: — Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать; Начать пользоваться сервисом -
Метод наименьших квадратов
|
|
Пусть переменная величина у, являющаяся функцией переменой величины х, измеряется при n различных значениях х, т.е. получают n экспериментальных точек: (х1, у1); (х2, у2); …(хn, уn). Будем считать, что зависимость у от х является функцией 
, вид которой зависит от параметров a1, a2, …, am. Величину этих параметров находят из условия минимума суммы квадратов:
.
Отсюда и название рассматриваемого метода. Из условия минимума S следует система уравнений
(i=1, 2, …, m), (1.19)
решая которую находят значения параметров 
.
Будем считать, что зависимость между х и у является линейной: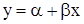 
.
Тогда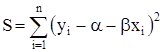 
. (1.20)
Подставляя сумму квадратов S, определяемую формулой (1.20) в уравнения (1.19) и решая их, найдем такие значения А и В параметров 
и 
, при которых сумма (1.20) минимальна, т.е. минимальна сумма квадратов отклонений экспериментальных точек (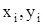
) от прямой линии 
.
Получим формулы:
; 
; (1.21)
; 
;
,
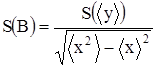где скобки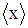 
означают среднее арифметическое величины х по всем n экспериментальным точкам (см. формулу 1.1). В формулах S(B) и S(A) - это выборочные оценки среднеквадратичных отклонений величин В и А. Отсюда полуширина 
доверительного интервала для вероятности Р выражается с помощью коэффициента Стьюдента:
,
где число степеней свободы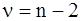 
(n - число экспериментальных точек).
Если значения 
большие, то вычисления по формулам (1.21) требуют высокой точности. Для уменьшения ошибок вычислений можно начало координат по оси Х перенести в точку .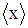
|
|