
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!
Вычисление арифметических выражений.
|
|
ЛЕКЦИЯ 1
Элементы программирования в среде MATLAB
Вычисление арифметических выражений.
1. Вычисления в среде MATLAB возможны в режиме командной строки (готовность системы к работе – знак > >) (см. рис. 1.1).
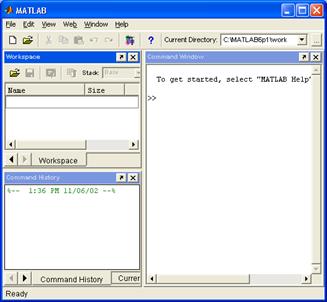
Рис. 1.1. Упрощенный интерфейс в системе MATLAB.
При работе с MATLAB в командном режиме действует простейший строчный редактор. Его команды перечислены в таблице.1.
Таблица 1.1. Команды строчного редактора MATLAB.
| Комбинация клавиш | Назначение |
| ® или Ctrl+b | Перемещение курсора вправо на один символ |
| или Ctrl+f | Перемещение курсора влево на один символ |
| Ctrl+® или Ctrl+r | Перемещение курсора вправо на одно слово |
| Ctrl+ или Ctrl+l | Перемещение курсора влево на одно слово |
| Home или Ctrl+a | Перемещение курсора в начало строки |
| End или Ctrl+e | Перемещение курсора в конец строки |
| и ¯ или Ctrl+р и Ctrl+n | Перелистывание предыдущих команд вверх или вниз для подстановки в строку ввода |
| Del или Ctrl+d | Стирание символа справа от курсора |
| или Ctrl+h | Стирание символа слева от курсора |
| Ctrl+k | Стирание до конца строки |
| Esc | Очистка строки ввода |
| Ins | Включение/выключение режима вставки |
| PgUp | Перелистывание страниц сессии вверх |
| PgDn | Перелистывание страниц сессии вниз |
Обратите особое внимание на применение клавиш курсора «вверх» и «вниз». Они используются для подстановки после маркера строки ввода > > ранее введенных строк, например с целью их исправления, дублирования или дополнения. При этом указанные клавиши обеспечивают перелистывание ранее введенных строк снизу вверх или сверху вниз. Такая возможность существует благодаря организации специального стека, хранящего строки с исполненными ранее командами.
2. Вычисления в среде MATLAB возможны в текстовых файлах с расширением.m (так называемые М-файлы, см. рис. 1.2). М-файлы могут быть созданы либо с помощью редактора М-файлов MATLAB, либо в другом редакторе, например Microsoft Word (с присвоением в дальнейшем этому файлу расширения.m). Последний подход является более эффективным, чем работа в командной строке MATLAB, особенно для задач, выполнение которых требует большого объема команд.
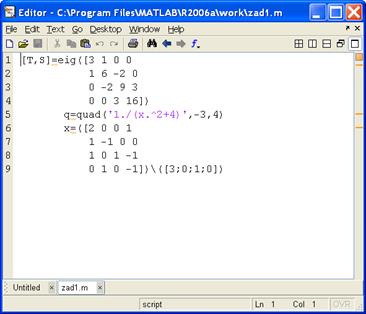
Рис.1.2. Окно редактора с текстом М-файла
М-файлы бывают двух типов: файл-программы (Script M-Files), содержащие последовательность команд и не имеющие входных и выходных аргументов, и файл-функции (Function M-Files), в которых описываются функции, определяемые пользователем.
Арифметические операции в MATLAB:
| + сложение | / деление слева направо |
| - вычитание | \ деление справа налево |
| * умножение | ^ возведение в степень |
Порядок (приоритетность) выполнения арифметических операций:
1. возведение в степень.
2. умножение и деление.
3. сложение и вычитание.
Выполнение операций одинакового приоритета происходит в порядке слева направо. Для изменения порядка выполнения ставятся круглые скобки.
Для работы с комплексными числами используются те же операции
(+, -, *, /, \), однако комплексные числа в выраженияхнеобходимо заключать в круглые скобки.
Любая переменная, используемая в выражениях, должна быть заранее определена. Знак равенства - оператор присваивания. Имя переменной не должно совпадать с именами встроенных процедур, функций и встроенных переменных системы и может содержать до 19 символов. Система различает большие и малые буквы в именах переменных.
Выражение в правой части оператора присваивания может быть числом, арифметическим выражением, строкой символов или символьным выражением. Символьная или строковая переменная берется в апострофы.
Если команда не содержит знака присваивания, то по умолчанию вычисленное значение присваивается специальной системной переменной ans. Полученное значение можно использовать в последующих вычислениях, но нужно помнить, что значение ans изменяется после каждого вызова команды без оператора присваивания.
Кроме того, в MATLAB существуют и другие системные переменные:
· i, j – мнимая единица (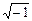 ) используется для создания мнимой части комплексных чисел (по умолчанию);
) используется для создания мнимой части комплексных чисел (по умолчанию);
· pi – число 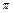 (3.141592653589793);
(3.141592653589793);
· eps – погрешность операций над числами с плавающей точкой;
· inf – машинный символ бесконечности (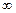 );
);
· NaN – неопределенный результат (0/0, 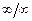 и т.д.);
и т.д.);
· realmin – наименьшее число с плавающей точкой (2.2251е-308);
· realmax – наибольшее число с плавающей точкой (1.7977е+308);
Все перечисленные переменные можно использовать в математических выражениях.
Ниже приведена таблица с некоторыми элементарными математическими функциями.
Таблица 1.2. Некоторые элементарные математические функции.
| Описание функции | Функция |
| синус числа x | sin(x) |
| косинус числа x | cos(x) |
| тангенс числа x | tan(x) |
| котангенс числа x | cot(x) |
| арксинус числа x | asin(x) |
| арккосинус числа x | acos(x) |
| арктангенс числа x | atan(x) |
| арккотангенс числа x | acot(x) |
| экспонента числа x | exp(x) |
| натуральный логарифм числа x | log(x) |
| корень квадратный из числа x | sqrt(x) |
| модуль числа x | abs(x) |
| действительная часть комплексного аргумента x | real(x) |
| мнимая часть комплексного аргумента x | imag(x) |
Пример 1.1. Вычислить следующие арифметические выражения.
1) 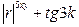 при
при 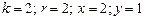
2) 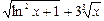 при
при 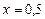
3) 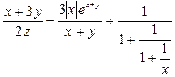 при
при 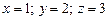
4) 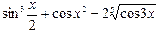 при
при 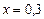
Для выполнения создается М-файл. Ниже приведен текст М-файла.
| k=2; r=2; x=2; y=1; r1=abs(r)^(5*x*y)+tan(3*k) x=.5; r2=sqrt(log(x)^2+1)+3*x^(1/3) x=1; y=2; z=3; r3=(x+3*y)/(2*z)-3*abs(x)*exp(x+y)/(x+y)+1/(1+1/(1+1/x)) x=0.3; r4=sin(x/2)^3+cos(x^2)-2*cos(3*x)^(1/5) |
Следует обратить внимание, что для просмотра результатов работы оператора знак «;» не ставится.
Результаты (в командном окне):
r1 =
1.0237e+003
r2 =
3.5978
r3 =
-18.2522
r4 =
-0.8193
|
|
