Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Поэлементная обработка изображений.

Сущность поэлементной обработки изображений сводится к следующему. Пусть , 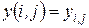– значения яркости исходного и получаемого после обработки изображений соответственно в точке кадра, имеющей декартовы координаты (номер строки) и (номер столбца). Поэлементная обработка означает, что существует функциональная однозначная зависимость между этими яркостями

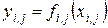, (1.1)

позволяющая по значению исходного сигнала определить значение выходного. В общем случае, как это учтено в данном выражении, вид или параметры функции 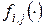, описывающей обработку, зависят от текущих координат. При этом обработка является неоднородной. Однако в большинстве практически применяемых процедур используется однородная поэлементная обработка. В этом случае индексы и j в выражении (1.1) могут отсутствовать. При этом зависимость между яркостями исходного и обработанного изображений описывается функцией:

(1.2)

одинаковой для всех точек кадра.

Линейное контрастирование изображения. Если для цифрового представления каждого отсчета изображения отводится 1 байт (8 бит) запоминающего устройства, то входной или выходной сигналы могут принимать одно из 256 значений. Обычно в качестве рабочего используется диапазон 0...255; при этом значение 0 соответствует при визуализации уровню черного, а значение 255 – уровню белого. Предположим, что минимальная и максимальная яркости исходного изображения равны x_min и x_max соответственно. Если эти параметры или один из них существенно отличаются от граничных значений яркостного диапазона, то визуализированная картина выглядит как ненасыщенная, неудобная, утомляющая при наблюдении. Пример такого неудачного представления приведен на рис. 1.1а, где диапазон яркостей имеет границы x_min = 180,
x_max = 240.

При линейном контрастировании используется линейное поэлементное преобразование вида

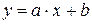_, (1.3)

параметры которого и определяются желаемыми значениями минимальной y_min и максимальной и y_max выходной яркости. Решив систему уравнений

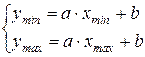
относительно параметров преобразования и , нетрудно привести (1.3) к виду:

.

Результат линейного контрастирования исходного изображения, представленного на рис. 1.1а, приведен на рис. 1.1б при y_min = 0 и
y_max = 255. Сравнение двух изображений свидетельствует о значительно лучшем визуальном качестве обработанного изображения. Улучшение связано с использованием после контрастирования полного динамического диапазона экрана, что отсутствует у исходного изображения.

а)	б)
Рис. 1.1. Пример линейного контрастирования:
а) исходное изображение; б) результат обработки

Преобразование гистограмм, эквализация. Все поэлементные преобразования изображений можно рассмотреть с точки зрения изменения плотности вероятности распределения яркостей исходного и получаемого изображений. Очевидно, что ни при одном из них плотность вероятности выходного продукта не будет совпадать с плотностью вероятности исходного изображения (за исключением преобразования ).

Определение вероятностных характеристик изображений, прошедших нелинейную обработку, является прямой задачей анализа. При решении практических задач обработки изображений может быть поставлена обратная задача: по известному виду плотности вероятности 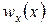и желаемому виду 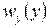определить требуемое преобразование 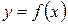, которому следует подвергнуть исходное изображение. В практике цифровой обработки изображений часто к полезному результату приводит преобразование изображения к равновероятному распределению. В этом случае

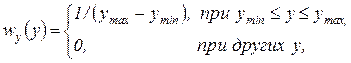(1.4)

где y_min и y_max – минимальное и максимальное значения яркости
преобразованного изображения.

Определим характеристику преобразователя, решающего данную задачу. Пусть x и y связаны функцией (1.2), а 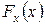и 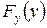– интегральные законы распределения входной и выходной величин. Учитывая (1.4), находим:

Подставляя это выражение в условие вероятностной эквивалентности

= ,

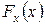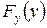после простых преобразований получаем соотношение

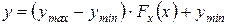, (1.5)

представляющее собой характеристику (1.2) в решаемой задаче. Согласно (1.5) исходное изображение проходит нелинейное преобразование, характеристика которого 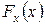определяется интегральным законом распределения самого исходного изображения. После этого результат приводится к заданному динамическому диапазону при помощи операции линейного контрастирования.

Таким образом, преобразование плотности вероятности предполагает знание интегрального распределения для исходного изображения. Как правило, достоверные сведения о нем отсутствуют. Использование для рассматриваемых целей аналитических аппроксимаций также малопригодно, т.к. их небольшие отклонения от истинных распределений могут приводить к существенному отличию результатов от требуемых. Поэтому в практике обработки изображений преобразование распределений выполняют в два этапа.

На первом этапе измеряется гистограмма исходного изображения. Для цифрового изображения, шкала яркостей которого, например, принадлежит целочисленному диапазону 0...255, гистограмма представляет собой таблицу из 256 чисел. Каждое из них показывает количество точек в кадре, имеющих данную яркость. Разделив все числа этой таблицы на общий размер выборки, равный числу используемых точек изображения, получают оценку распределения вероятностей яркости изображения. Обозначим эту оценку 0 £ j £ 255. Тогда оценка интегрального распределения получается по формуле:

_.

На втором этапе выполняется само нелинейное преобразование (1.2), обеспечивающее необходимые свойства выходного изображения. При этом вместо неизвестного истинного интегрального распределения используется его оценка, основанная на гистограмме. С учетом этого все методы поэлементного преобразования изображений, целью которых является видоизменение законов распределения, получили название гистограммных методов. В частности, преобразование, при котором выходное изображение имеет равномерное распределение, называется эквализацией (выравниванием) гистограмм.

Отметим, что процедуры преобразования гистограмм могут применяться как к изображению в целом, так и к отдельным его фрагментам. Последнее может быть полезным при обработке нестационарных изображений, содержание которых существенно различается по своим характеристикам на различных участках. В этом случае лучшего эффекта можно добиться, применяя гистограммную обработку к отдельным участкам.

Использование соотношений (1.4), (1.5), справедливых для изображений с непрерывным распределением яркости, является не вполне корректным для цифровых изображений. Необходимо иметь в виду, что в результате обработки не удается получить идеальное распределение вероятностей выходного изображения, поэтому полезно проводить контроль его гистограммы.

На рис. 1.2 приведен пример эквализации, выполненной в соответствии с изложенной методикой. Характерной чертой многих изображений, получаемых в реальных изображающих системах, является значительный удельный вес темных участков и сравнительно малое число участков с высокой яркостью.

а)	б)
Рис. 1.2. Пример эквализации изображения:
а) исходное изображение; б) результат обработки

Эквализация призвана откорректировать картину, выровняв интегральные площади участков с различными яркостями. Сравнение исходного (рис. 1.2а) и обработанного (рис. 1.2б) изображений показывает, что происходящее при обработке перераспределение яркостей приводит к улучшению визуального восприятия.