Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Методичні вказівки до виконання практичної роботи. МЕТА:навчитися використовувати жорданові виключення для розв’язування системи лінійних рівнянь методом оберненої матриці.
|
|
Практична робота № 4
Тема: РОЗВ′ ЯЗАННЯ СИСТЕМ ЛІНІЙНИХ РІВНЯНЬ МЕТОДОМ ЖОРДАНОВИХ ВИКЛЮЧЕНЬ ТА ОБЕРНЕНОЇ МАТРИЦІ
МЕТА: навчитися використовувати жорданові виключення для розв’язування системи лінійних рівнянь методом оберненої матриці.
Хід роботи
1. Знайти матрицю, що є оберненою матриці коефіцієнтів системи рівнянь за варіантом завдання (Таблиця 1).
2. Розв’язати систему лінійних рівнянь методом оберненої матриці.
3. Розв’язати систему лінійних рівнянь методом жорданових виключень.
4. Порівняти результати та перевірити їх правильність за допомогою блока Given – Find програмі MathCad.
Методичні вказівки до виконання практичної роботи
Кроком звичайного жорданового виключення, здійсненим над даною таблицею з дозволяючим елементом aij≠ 0, з i-дозволяючою строкою та j-дозволяючим стовпчиком назвемо операцію рішення рівняння відносно xj
bi=ai1x1+ai2x2+…+aijxj+…+ainxn
підстановки цього рішення в початкову систему з запису знов отриманої системи у вигляді нової таблиці.
Один крок жорданового виключення переводить початкову таблицю у нову за схемою:
1.Дозволюячий елемент замінюється на 1.
2.Інші елементи дозволяючого стовпчика j залишаються без змінень.
3.Інші елементи дозволяючої строки i міняють знак на протилежний.
4.Усі інші елементи brs вираховуються за формулою
brs=arsaij-arjais, i≠ r j≠ s
5.Усі елементи нової таблиці діляться на дозволюячий елементaij.
Зробив послідовно n-кроків Жорданових виключень з дозволяючи ми стовпчиками, які відрізняються від стовпчиків вільних членів і викреслюючи після кожного кроку стовпчик коеффіціентів під переброшеним нагору таблиці нулемБ отримаємо кінцеве рішення у вигляді:
x1 = a1
x2 = a2
…
xn =an
Метод оберненої матриці рішення СЛУ полягає у наступному: знаходиться обернена матриця A-1 до матриці коеффіціентів системи методом Жорданових рішень.
| x1 | x2 | x3 | b |
| 0, 67 | 0, 07 | 0, 17 | -0, 32 |
| 0, 17 | 0, 12 | 0, 73 | -0, 40 |
| 0, 05 | 0, 36 | 0, 12 | -0, 30 |
Приклад 1. Знайти матрицю, що є оберненою матриці коефіцієнтів системи рівнянь.
| x1 | x2 | x3 |
| b1 | 0, 67 | 0, 07 | 0, 17 |
| b2 | 0, 17 | 0, 12 | 0, 73 |
| b3 | 0, 05 | 0, 36 | 0, 12 |
| b1 | x2 | x3 | |
| x1 | 1, 492537 | -0, 10448 | -0, 25373 |
| b2 | 0, 253731 | 0, 102239 | 0, 544776 |
| b3 | 0, 074627 | 0, 354776 | 0, 107313 |
| b1 | b2 | x3 | |
| x1 | 1, 751825 | -1, 0219 | 0, 302974 |
| x2 | -2, 48175 | 9, 781022 | -5, 32847 |
| b3 | -0, 80584 | 3, 470073 | -1, 7831 |
| b1 | b2 | b3 | |
| x1 | 1, 614901 | -0, 43228 | -0, 16991 |
| x2 | -0, 07365 | -0, 58866 | 2, 988317 |
| x3 | -0, 45193 | 1, 946091 | -0, 56082 |
Результат з MathCad
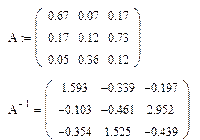
Приклад 2. Розв’язати систему лінійних рівнянь методом оберненої матриці.
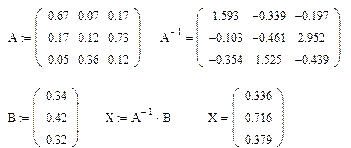
Приклад 3. Розв’язати систему лінійних рівнянь методом жорданових виключень.
| x1 | x2 | x3 | ||
| 0, 67 | 0, 07 | 0, 17 | -0, 32 | |
| 0, 17 | 0, 12 | 0, 73 | -0, 4 | |
| 0, 05 | 0, 36 | 0, 12 | -0, 3 | |
| x2 | x3 | |||
| x1 | -0, 10448 | -0, 25373 | 0, 477612 | |
| * | 0, 102239 | 0, 544776 | -0, 31881 | |
| * | 0, 354776 | 0, 107313 | -0, 27612 | |
| x3 | ||||
| x1 | * | * | 0, 302974 | 0, 151825 |
| x2 | * | -5, 32847 | 3, 118248 | |
| * | * | -1, 7831 | 0, 830161 | |
| x1 | * | * | * | 0, 292881 |
| x2 | * | * | * | 0, 637465 |
| x3 | * | * | * | 0, 465572 |
Приклад 4. Порівняти результати та перевірити їх правильність за допомогою блока Given – Find програмі MathCad.
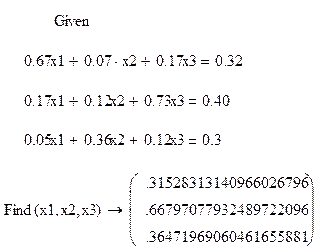
Між значеннями отриманними методом Жорданових виключень, та прорахованими у MathCad-і є невеличкі розбіжності, з-за похибки цього методу.
|
|