Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Метод потенциалов

Пусть имеется опорное решение (опорный план). Каждому i-му поставщику и j-му потребителю поставим в соответствие числа u_i и v_jкоторые называются потенциалами.

Значения потенциалов находят из системы уравнений, каж­дое из которых получено для заполненных клеток опорного ре­шения: u_i + v_j= c_ij. Одному из потенциалов дается произвольное значение, например u_i = 0 или 1, по которому находят все остальные потенциалы.

Для свободных клеток находят оценки по формуле 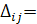c_ij – (u_i + v_j). Если все оценки > 0, то опорное решение является оптимальным. Если хотя бы одна из оценок < 0, то опорное решение оптимальным не является и его можно улуч­шить. Для этого из всех оценок < 0 выбираем наибольшее по абсолютной величине и производим перерасчет плана перевозок, т. е. осуществляем переход к другому опорному решению.

Для этого перехода необходимо для выбранной свободной клетки с < 0 построить многоугольник - контур, одна из вершин кото­рого находится в выбранной клетке, а все остальные вершины находятся в занятых клетках (вершин всегда чётное количество). При этом все углы в контуре прямые и обязательно должен соблюдаться баланс в столбцах и строках таблицы, для этого свободной вершине присваивается знак «+», знаки остальных вершин чередуются. На каждой стороне контура может находится две заполненые вершины, кроме того одна вершина лежит в заполняемой пустой клетке.

а) Рассмотрим нахождение оптимального плана, взяв за опорное решение, полученное применением метода «северо-западного» угла (см. табл. 1). Добавим в табл. 1 строку v_j и столбец u_i.

Таблица 5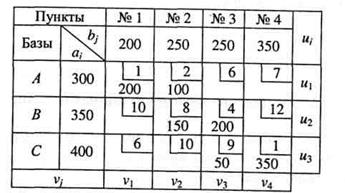

Для нахождения потенциалов необходимо решить систему, составленную для занятых клеток таблицы 5 по формуле ui + vj= cij

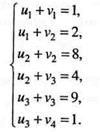
Положим u₁ = 1, тогда v₁ = 0, v₂ = 1, и₂ = 7, v₃ = -3, и₃ = 12, v₄= -11. Для свободных клеток найдем оценки по формуле 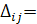c_ij – (u_i + v_j):

Так как среди оценок есть две отрицательные: = -6 и = -3, то опорное решение оптимальным не является и его можно улучшить. Наименьшая из отрицательных оценок (наи­большая по абсолютной величине) = -6. Данная оценка соот­ветствует клетке (3; 1). Следовательно, можно попытаться умень­шить L, увеличив х₃₁. Положим х₃₁ = λ.

Построим контур, одна из вершин которого находится в клетке (3; 1), а все другие вершины находятся в занятых клетках и поскольку суммы значений неизвестных по строкам и столбцам должны остаться неизменными, необходимо произвести следующий балансовый пересчет (табл. 6).

Таблица 6

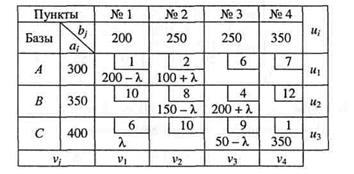
Для определения значения λ рассмотрим значения в клетках, из которых планируется переместить груз. Это клетки: (1; 1), (2; 2) и (3; 3). Значение λ определяется как минимальное из решений уравнений:

200 - λ = 0, 150 - λ = 0 и 50 - λ = 0.

Минимальное решение соответствует λ = 50.

При этом значении λ получаем второе опорное решение (табл. 7).

Талица 7

Этому опорному решению соответствует значение

L = 1∙ 150 + 2∙ 150 + 8∙ 100 + 4∙ 250 + 6∙ 50 + 1∙ 350 = 2900 (денежных единиц).

Найдем потенциалы из решения системы, составленной для занятых клеток табл. 7.

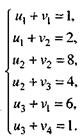
Положим u1 = 1, тогда v1 = 0, v2 = 1, и2 = 7, v3 = -3, и3 = 6, v4 = -5. Для свободных клеток найдем оценки :

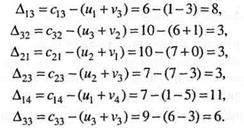
Так как среди оценок нет отрицательных, то полученное опорное решение

х ₁₁ = 150, х₁₂ = 150, х₂₂ = 100, х₂₃= - 250, х₃₁ = 50 и х₃₄ = 350 является оптимальным и

L =1∙ 150 +2∙ 150 + 8∙ 100 + 4∙ 250 + 6∙ 50 +1∙ 350 = 2900 (д. ед.).

Ответ: х ₁₁ = 150, х₁₂ = 150, х₂₂ = 100, х₂₃= - 250, х₃₁ =50, х₃₄ = 350, L_min = 2900 (д. ед.)