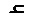Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Критическим условиям самовозгорания твердых дисперсных материалов методом касательных
|
|
Склонность к самовозгоранию является свойством вещества, проявляющимся в способности загораться при отсутствии внешнего источника зажигания за счет внутренних экзотермических реакций.
Современные методы определения склонности веществ к самовозгоранию основаны на анализе кривых температура – время или критических условий самовозгорания. Наибольшее распространение получили термографические методы.
Критические условия при тепловом самовозгорании и самовоспламенении можно записать предельным равенством адиабатической скорости самонагревания (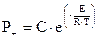 ) критической температуре Тв и виртуальной скорости охлаждения Р- в стадии регулярного теплового режима первого рода (
) критической температуре Тв и виртуальной скорости охлаждения Р- в стадии регулярного теплового режима первого рода (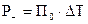 ) при этой же температуре (Тв), т.е.
) при этой же температуре (Тв), т.е.
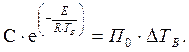 (8)
(8)
Равенство (8) справедливо для образцов с различными темпами охлаждения. Поэтому, определив критические температуры самовозгорания нескольких образцов (не менее 4-5), при известных их темпах охлаждения методом касательных можно определить кинетические параметры Е и С, методика определения которых состоит в следующем.
Экспериментально определяют несколько (не менее 4-5) критических температур самовозгорания Т0, i образцов (навесок) с различными темпами охлаждения П0 i. Численное значение критических температур Т0, i откладывают на горизонтальной оси (оси температур). Из точек, соответствующих критическим температурам (Т0, i) проводят прямые охлаждения под углами к оси иксов (Т), с тангенсами, равными темпам охлаждения (П0). Затем проводят огибающую кривую таким образом, чтобы она по возможности касалась всех графиков охлаждения. Согласно теории теплового самовозгорания эта кривая является графиком искомой функции Р+(Т), описывающей температурную зависимость адиабатической скорости самонагревания.
При тепловом механизме самовозгорания эта зависимость описывается экспонентой Аррениуса
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
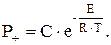
Кинетические параметры Е и С, входящие в это уравнение, определяют следующим образом.
Значение координат точек касания графиков самонагревания Р+(Т) с графиком охлаждения Р = П0·∆ Т заносят в таблицу.
По этим точкам в координатах: обратная температура (ось Х) – натуральный логарифм адиабатической скорости самонагревания (ось У) строят прямую
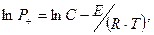 (9)
(9)
С помощью построенного графика энергию активации Е рассчитывают по формуле:
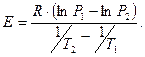 (10)
(10)
Затем значение Е подставляют в (9) и вычисляют lnC.
Порядок расчета Е и С методом касательных рассмотрен ниже на конкретном примере.
УСЛОВИЕ ЗАДАЧИ №2
Определить кинетические параметры энергии активации (Е) и предэкспоненциального множителя (С) в уравнении Аррениуса по критическим условиям самовозгорания твердых дисперсных материалов методом касательных. Исходные данные для решения задачи приведены в таблице 2.1.
ИСХОДНЫЕ ДАННЫЕ
Таблица 2.1
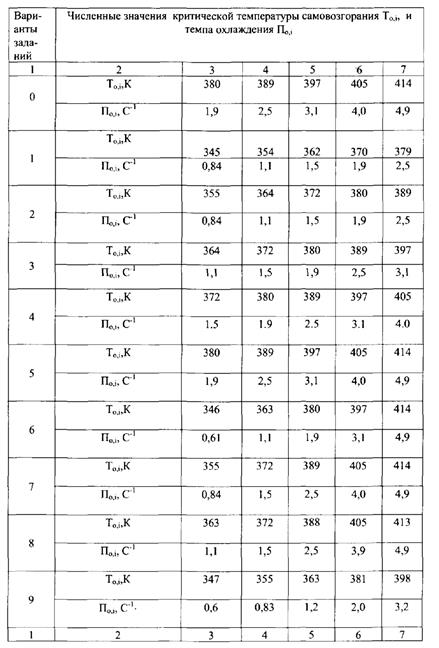
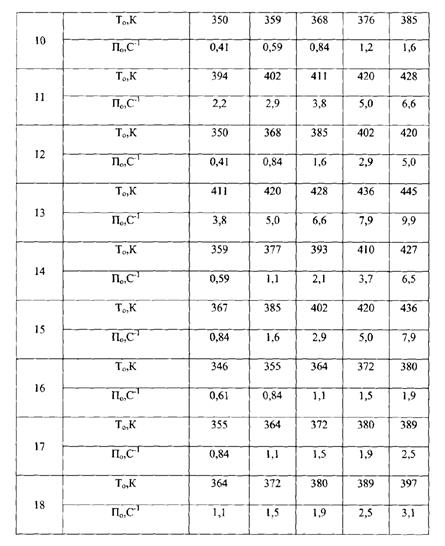
Примечание: Построение графиков производится на миллиметровой бумаге, которая вклеивается в тетрадь
КОНТРОЛЬНЫЙ ПРИМЕР
Для того, чтобы построить график адиабатической скорости самонагревания в координатах Р-, Т0, i (как показано на рис. 2.1), необходимо взять из индивидуального задания (таблица 2.1) значения критических температур самонагревания (Т0, i, К) и отложить на горизонтальной оси Т0, i все пять точек. Масштаб горизонтальной оси принять таким образом, чтобы от последнего пятого значения температуры самовозгорания вправо оставалось 1/3 тетрадного листа (рис. 2.1).
Например: Вариант n
| Т0, i, К | |||||
| П0, с-1 | 0, 62 | 0, 84 | 1, 10 | 1, 40 | 1, 90 |

Рис. 2.1.
Чтобы провести прямые охлаждения, необходимо проделать следующее графические и арифметические действия:
- взять ∆ Т (произвольно, любое целое число);
- отложить на оси Т0, i значение (Т0, i +∆ Т);
- восстановить из полученных точек перпендикуляры к оси Т0, i;
- найти произведения 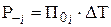 (полученных значений будет также пять);
(полученных значений будет также пять);
- отложить вертикально вверх на соответствующих перпендикулярных прямых полученные значения Р- i.
Принимаем ∆ Т =20 0С и отложим на оси Т0, i значения Т0, i +∆ Т (рис. 2.2).
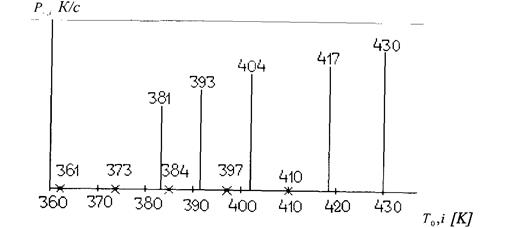
Рис 2.2
Находим произведения П0j·∆ Т:
первая точка: 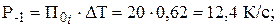
вторая точка: 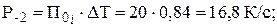
третья точка: 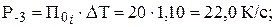
четвертая точка: 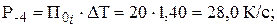
пятая точка: 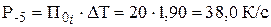
Откладываем вверх по вертикали полученные значения, причем масштаб по вертикальной оси выбирается таким образом, чтобы от последнего полученного значения (Р-5 =38, 0) оставалось 1/2 тетрадного листа (рис 2.2).
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
Через две точки строим прямые охлаждения по уравнению 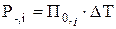 (рис. 3.3). Построение прямой охлаждения для первой точки (Р-i) проводят следующим образом: соединяем точку со звездочкой (361 К) с координатой точки Р-, 1 =12, 4К/с на перпендикуляре 381 К. Так получаем прямую охлаждения 1 (см. рис. 2.3). Аналогично строим прямые охлаждения для 2, 3, 4 и 5 прямой.
(рис. 3.3). Построение прямой охлаждения для первой точки (Р-i) проводят следующим образом: соединяем точку со звездочкой (361 К) с координатой точки Р-, 1 =12, 4К/с на перпендикуляре 381 К. Так получаем прямую охлаждения 1 (см. рис. 2.3). Аналогично строим прямые охлаждения для 2, 3, 4 и 5 прямой.
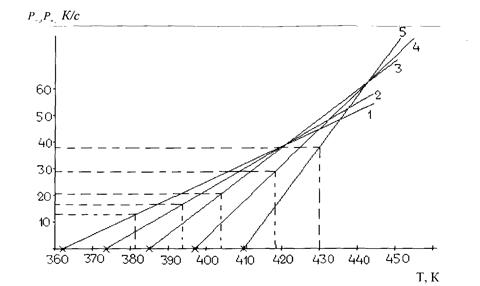
Рис 2.3
После этого строим кривую температурной зависимости адиабатической скорости самонагревания
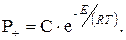
Эта кривая должна проходить таким образом, чтобы она касалась прямых охлаждения только в одной точке и не пересекала этих прямых (рис 2.4).
Кривая адиабатической скорости самонагревания строится следующим образом. На прямых охлаждения (1, 2, 3, 4 и 5) определяем при помощи лекала возможные точки касания экспоненты и намечаем их координаты. Так для прямой охлаждения 1 экспонента коснется в точке Р+, 1=16, 9, Т0, 1=387; для прямой 2 – Р+, 2 =31, Т0, 2=408; для прямой 3 – Р+, 3 =49, 6, Т0, 3=428; для прямой 4 – Р+, 4 =66, 2, Т0, 4=443; для прямой 5 – Р+, 5 =88, 0, Т0, 5=455.
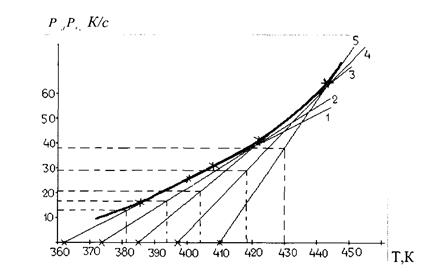
Рис 2.4 График температурной зависимости адиабатической
скорости самонагревания.
Через эти точки проводим по лекалу касательную, получаемую в виде экспоненты, которая описывается зависимостью (8).
Координаты получаемых точек касания кривой адиабатической скорости самонагревания с прямыми охлаждения заносим в таблицу 2.2.
Таблица 2.2
| Температура охлаждения П0, с-1 | Температура Т, К (из графика) | Р+, К/с (из графика) | 103/Т, К-1 (расчетом) | ln (Р+) (расчетом) |
| 0, 62 0, 84 1, 10 1, 40 1, 90 | 16, 9 31, 0 49, 6 66, 2 88, 0 |
Путем вычислений заполняем оставшиеся две графы таблицы 2.2 по нижеприведенным соотношениям:
1. 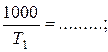
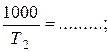 и т.д.
и т.д.
2. 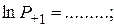
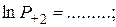 и т.д.
и т.д.
Результаты вычислений заносим в последние две графы таблицы 2.3.
Таблица 2.3
| Температура охлаждения П0, с-1 | Температура Т, К (из графика) | Р+, К/с (из графика) | 103/Т, К-1 (расчетом) | ln (Р+) (расчетом) |
| 0, 62 0, 84 1, 10 1, 40 1, 90 | 16, 9 31, 0 49, 6 66, 2 88, 0 | 2, 5839 2, 4509 2, 3364 2, 2573 2, 1978 | 2, 8273 3, 4339 3, 9039 4, 1926 4, 4773 |
По данным последних двух колонок (табл. 2.3) строим график в координатах ln(Р+), 103/Т, К, как показано на рис. 3.5.
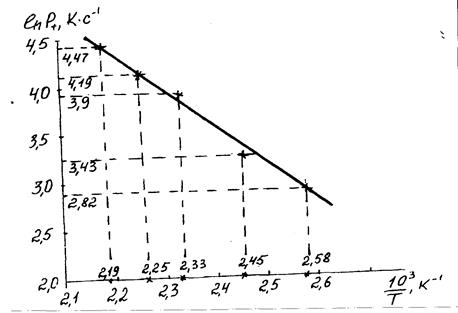
Рис. 2.5
По полученным на графике (рис. 2.5) точкам строим прямую. Затем на этой прямой выбираем две характерные точки (любые) и координаты этих точек подставляем в следующие соотношения:
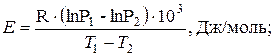
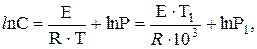
откуда находим С:
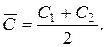

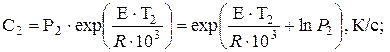
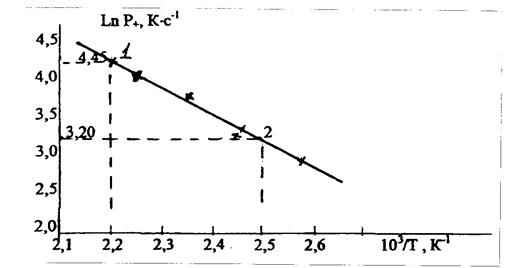
Рис. 3.6 График адиабатической скорости самонагревания
в координатах Аррениуса.
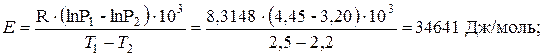
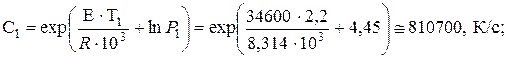
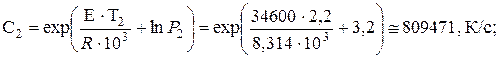
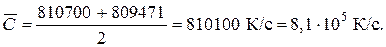
ВЫВОД ПО РАБОТЕ:....................................
Удельная поверхность геометрических фигур
| Фигура | Объем - V, поверхность - F | |||||||
 Шар Шар
| 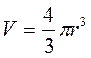
| |||||||
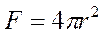
| ||||||||
         Цилиндр Цилиндр
h=r | 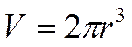
| |||||||
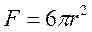
| ||||||||
      Цилиндр Цилиндр
h=2r
| 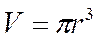
| |||||||
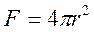
| ||||||||
              Цилиндр
h=3r Цилиндр
h=3r
| 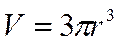
| |||||||
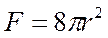
| ||||||||
 Куб
r – ребро куба Куб
r – ребро куба
| 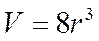
| |||||||
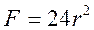
|
|
|

 r - радиус
r - радиус