Квадратичные формы, их преобразования. Рязань 2012 Тема 10. Квадратичные формы

ЛЕКЦИИ ПО ДИСЦИПЛИНЕ

«ЛИНЕЙНАЯ АЛГЕБРА»

Направление 080100

«Экономика»

Очная форма обучения

Рязань 2012
Тема 10. Квадратичные формы

Квадратичные формы, их преобразования

Определение 6.1. Квадратичной формой от n переменных называется однородный многочлен второй степени

. (6.1)

Запись вида (6.1) называется координатной формой записи квадратичной формы (с приведенными подобными членами).

Если в 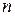-мерном линейном пространстве выбран некоторый базис, то переменные можно интерпретировать как координаты вектора в этом базисе, при этом координатный вектор-столбец. Если обозначить через (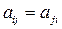, ) матрицу 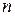-го порядка из коэффициентов 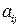, то квадратичную форму (5.1) можно записать в матричной форме

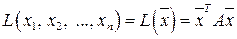. (6.2)

При этом квадратная матрица называется матрицей квадратичной формы. В силу условия 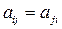при всех она является симметрической матрицей. В самом деле, имеем

.

Определение 6.2. Рангом квадратичной формы (6.2) называется ранг её матрицы . При этом пишут

.

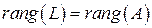Определение 6.3. Квадратичная форма (6.2) называется невырожденной, если соответствующая ей матрица является невырожденной. При этом . В противном случае (если 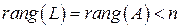) квадратичная форма (6.2) называется вырожденной.

Рассмотрим, как меняются коэффициенты квадратичной формы (6.2) при линейной замене переменных. Пусть переменные заменяются на переменные по формулам

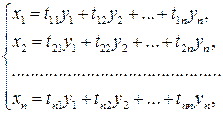(6.3)

где некоторые числа.

Если обозначить 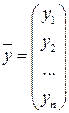, , 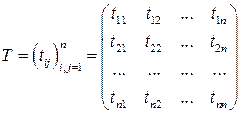то формулы (6.3) можно переписать в матричной форме

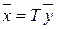. (6.4)

Определение 6.4. Преобразование (6.4) называется линейным преобразованием. Матрица называется матрицей линейного преобразования. При этом, если матрица является неособенной матрицей, то преобразование (6.4) называется неособенным линейным преобразованием.

Применим преобразование (6.4) к форме (6.2):

,

где обозначена матрица .

Итак, если к квадратичной форме (6.2) применить линейное преобразование (6.4), то получим квадратичную форму

(6.5)

Если рассматривать 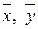как координатные вектор-столбцы вектора в базисах 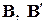соответственно, то матрица является матрицей перехода от базиса к базису (при этом преобразование (6.4) будет неособенным линейным преобразованием).

Наибольший интерес для дальнейшего изучения квадратичных форм представляют такие неособенные преобразования (6.4), которые приводят квадратичную форму (6.2) к квадратичной форме (6.5) с диагональной матрицей :

.

Определение 6.5. Говорят, что квадратичная форма имеет канонический вид, если она содержит только квадраты переменных и не содержит парных произведений разноименных переменных:

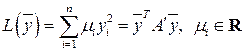. (6.6)

При этом базис, в котором квадратичная форма имеет канонический вид (6.6), называется диагонализирующим базисом. Задача нахождения диагонализирующего базиса называется задачей диагонализации квадратичной формы.

Если (6.2) есть невырожденная квадратичная форма (), то в результате неособенного линейного преобразования (6.4) матрица будет являться неособенной матрицей (при неособенных линейных преобразованиях ранг матрицы не изменяется). То есть при всех : . Если же квадратичная форма (6.2) является вырожденной и имеет ранг 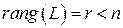, то диагонализирующий базис (если он существует) можно выбрать так, что матрица в этом базисе имеет следующий диагональный вид:

, , .

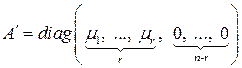Позже будет показано, что для любой квадратичной формы всегда можно найти диагонализирующий базис, в котором эта форма имеет канонический вид (6.6).

Пример 6.1. Задана квадратичная форма от трех переменных 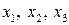в стандартном базисе пространства :

.

Найти вид этой квадратичной формы в базисе, если задана матрица перехода

.

Решение. Матрица 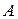квадратичной формы имеет вид

.

Тогда по формуле (6.5) определяем матрицу этой формы в новом базисе

.

В новом базисе переменных 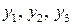квадратичная форма имеет канонический вид

.
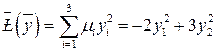