
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!
Работа 5.1
|
|
О П Т И К А
ИНТЕРФЕРЕНЦИЯ СВЕТА. ОПЫТ ЮНГА
Цель работы: 1) наблюдение интерференционной картины от двух параллельных щелей в монохроматическом свете;
2) определение длины волны лазерного излучения.
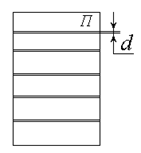 |
Схема экспериментальной установки
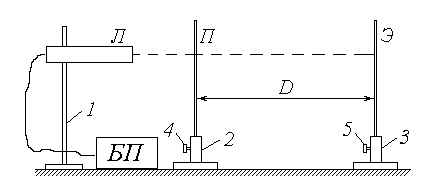
1, 2, 3 – штативы; 4, 5 – регулировочные винты; Л – газовый лазер;
БП – блок питания лазера; П – пластинка со щелями; Э – экран
Описание установки и методики измерений
Источником монохроматического излучения в данной работе является газовый лазер Л, закрепленный горизонтально в штативе 1; включение лазера осуществляется тумблером на панели блока питания БП. В штативе 2 размещена непрозрачная зачерненная пластинка П, на которую нанесены несколько пар горизонтальных щелей, расположенных на малом расстоянии d друг от друга (фронтальное изображение пластинки со щелями дано на схеме установки справа). Ослабив регулировочный винт 4, можно перемещать пластинку П по вертикали, направляя лазерный луч на различные пары щелей. Интерференционная картина наблюдается на экране Э, закрепленном в штативе 3 и удаленном на расстояние D от пластинки со щелями (на схеме плоскости пластинки П и экрана Э перпендикулярны плоскости чертежа).
Газовый лазер испускает узкий пучок монохроматического (красного) цвета. Как известно, свет представляет собой электромагнитную волну; в случае узкого пучка фронт этой волны можно считать плоским. Уравнение плоской волны имеет вид
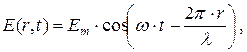 (1)
(1)
где E (r, t) – проекция светового вектора (напряженности электрического поля) на плоскость его колебаний в точке, находящейся на расстоянии r от источника света в момент времени t; Em – амплитуда колебаний; w – циклическая частота; l – длина волны излучения.
Из выражения (1) следует, что значение Е определяется фазой колебаний
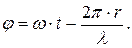 (2)
(2)
 Попадая на пластинку П, луч лазера проходит через две узкие и близко расположенные друг к другу щели S 1 и S 2 (рис. 32). Каждую из этих щелей можно рассматривать как источ-ник света, причем благо-даря одинаковой частоте и постоянной во времени разности фаз эти источ-ники когерентны. Расхо-дящиеся от них световые пучки перекрываются, и на экране Э можно на-блюдать результат их на-ложения, т.е. картину интерференции.
Попадая на пластинку П, луч лазера проходит через две узкие и близко расположенные друг к другу щели S 1 и S 2 (рис. 32). Каждую из этих щелей можно рассматривать как источ-ник света, причем благо-даря одинаковой частоте и постоянной во времени разности фаз эти источ-ники когерентны. Расхо-дящиеся от них световые пучки перекрываются, и на экране Э можно на-блюдать результат их на-ложения, т.е. картину интерференции.
В произвольную точку М экрана приходят две волны и возбуждают колебания
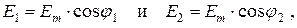
разность фаз которых, согласно (2), равна
 (3)
(3)
где D = (r 1 – r 2) – разность хода лучей от источников до точки М. Амплитуда результирующего колебания в точке М определяется выражением

а интенсивность света в данной точке
 (4)
(4)
где I 0 – интенсивность от каждого из источников в отдельности.
Таким образом, результат интерференции зависит от величины cos d. При cos d = - 1 интенсивность I = 0; совокупность таких точек на экране образует ряд темных полос. При cos d = 1 интенсивность максимальна: I = I max = 4 I 0 – такие точки образуют светлые полосы.
Как известно, cos d = 1 при d = 2 kp и cos d = - 1 при d = (2 k + 1) p, где k Î Z. С учетом выражения (3) получим условия наблюдения максимумов
D = kl (5)
и минимумов
D = (2 k + 1)× 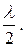 (6)
(6)
Найдем положение соответствующих точек, т.е. координаты светлых и темных полос на экране. Направим ось Oy вертикально в плоскости экрана Э; начало координат совместим с центром наблюдаемой картины (см. рис. 32). Воспользуемся теоремой Пифагора:
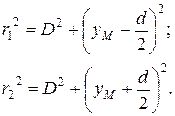
Вычитая почленно первое уравнение из второго, получим
r 12 – r 12 = 2 yd
или
(r 2 + r 1)(r 2 - r 1) = 2 yd (7)
(здесь и в дальнейшем индекс «М» у координаты исследуемой точки опущен).
Расстояние между щелями d составляет менее 1 мм, а расстояние от щелей до экрана D – несколько десятков сантиметров. Поэтому можно с достаточной степенью точности положить величину (r 2 + r 1)» 2 D. Учитывая также, что (r 2 - r 1) = D, преобразуем (7) к виду
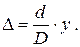 (8)
(8)
Координаты светлых полос найдем, подставляя (8) в условие максимума (5):
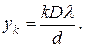
Ширина интерференционной полосы D y (расстояние между соседними максимумами или минимумами) может быть определена как
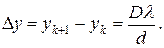
Полученное соотношение позволяет по известным расстояниям d, D и D y найти длину волны излучения:
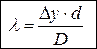 . (9)
. (9)
Примерный вид интерференционной картины от двух щелей показан на рис. 33. Для практического определения ширины интерференционной 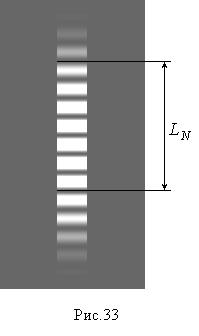 полосы необходимо измерить расстояние LN , на котором укладывается целое число N светлых полос. Ширина полосы находится из очевидного соотношения
полосы необходимо измерить расстояние LN , на котором укладывается целое число N светлых полос. Ширина полосы находится из очевидного соотношения
 (10)
(10)
(чем больше N, тем точнее будет определена величина D y; в приведенном на рис. 33 примере N = 7).
|
|
