Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Решение матричного уравнения в Excel.

КВАДРАТИЧНЫЕ ФОРМЫ

Целью лабораторной работы “ Квадратичные формы ” является освоение матричных функций Excel и VBA.

Выполнение лабораторной работы предполагает знание элементов векторного анализа, в частности, матричных операций.

Лабораторная работа “Квадратичные формы” состоит из двух частей, в первую часть входят:

– решение матричного уравнения в Excel;

– решение матричного уравнения в Excel с предварительным преобразованием;

– вычисление квадратичной формы в Excel;

– вычисление квадратичной формы с использованием матричных функций Excel;

– вычисление квадратичной формы с использованием матричных функций VBA,

а во вторую:

– операции над массивами в Excel;

– операции над массивами в VBA.

Критерием правильности решений матричных уравнений являются результаты проверки подстановкой найденных значений корней в исходные уравнения.

Критерием правильности вычислений квадратичной формы является совпадение полученных значений трех способов вычислений.

Выполнение лабораторной работы начинается с внесения исходных данных задания в соответствующие ячейки таблицы Excel, в выбранной адресации:

– значения матрицы А – А8: D11;

– значения вектора B – F8: F11;

– значения вектора Y – H8: H11, рис. 6.1.

Часть первая

Решение матричного уравнения в Excel.

Так как решением матричного уравнения АХ=В является вектор Х=А^-1В, то необходимо сформировать обратную матрицу А^-1, это выполняется в ячейках A14: D17, для чего:

- выделить A14: D17,

- через мастер функций f_x вызвать матричную операцию МОБР, в окне “массив” которой указать адрес исходной матрицы А – А8: D11;

- затем одновременно нажать клавиши Ctrl-Shift-Enter.

В результате в ячейках A14: D17 появятся значения элементов обратной матрицы А^-1, рис. 6.2., а для любой ячейки диапазона A14: D17 в строке состояний подтверждение выполнения матричной операции {=МОБР(A8: D11)}.

Так как результатом произведения исходной матрицы А на обратную матрицу А^-1 является единичная матрица E, то для проверки правильности значений элементов полученной обратной матрицы необходимо:

- выделить F14: I17;

- через мастер функций f_x вызвать матричную операцию МУМНОЖ, в окне рис. 6.3 “Массив1” которой указать адрес исходной матрицы А – А8: D11, а в окне “Массив2” которой указать адрес обратной матрицы А^-1 – А14: D17;

- затем одновременно нажать клавиши Ctrl-Shift-Enter.

В результате в ячейках F14: I17 появятся значения элементов единичной матрицы E, рис. 6.2., а для любой ячейки диапазона F14: I17 в строке состояний подтверждение выполнения матричной операции {=МУМНОЖ(A8: D11; A14: D17)}

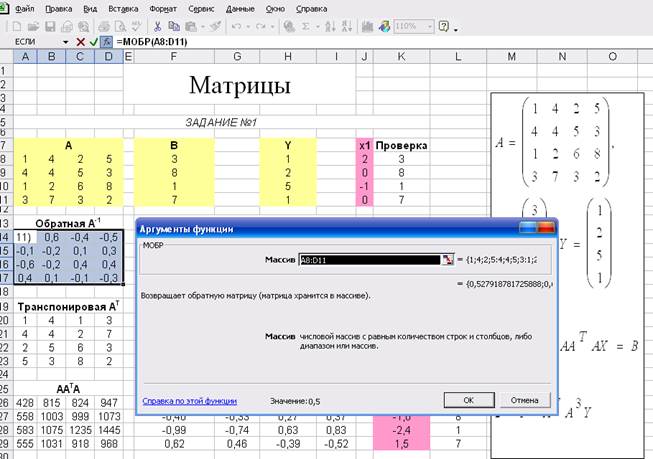
Рис. 6.1.

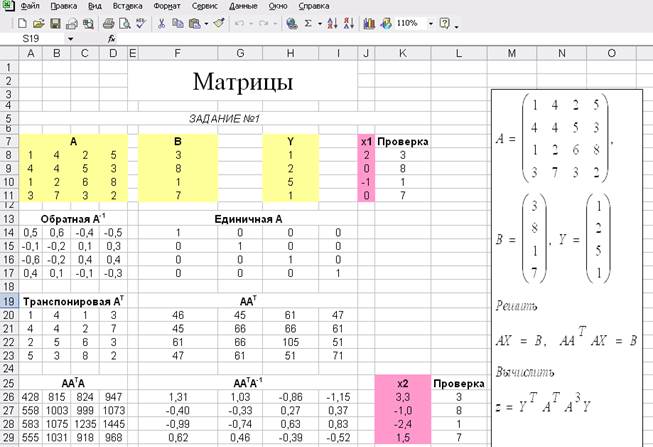
Рис. 6.2.

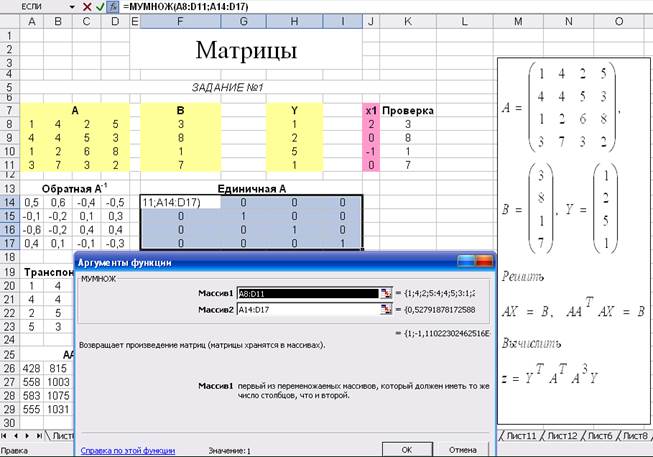
Рис. 6.3.

Для получения вектора решений Х=А^-1В необходимо:

- выделить J8: J11;

- через мастер функций f_x вызвать матричную операцию МУМНОЖ, в окне “Массив1” которой указать адрес обратной матрицы А^-1 – F14: I17, а в окне “Массив2” которой указать адрес вектора свободных членов B – F8: F11;

- затем одновременно нажать клавиши Ctrl-Shift-Enter.

В результате в ячейках J8: J11 появятся значения элементов вектора решений X , рис. 6.2., а для любой ячейки диапазона J8: J11 в строке состояний подтверждение выполнения матричной операции {=МУМНОЖ(F14: I17; F8: F11)}.

Для проверки истинности значений элементов полученного вектора решений X необходимо подставить полученные значения в исходное уравнение АХ=В, для чего следует:

- выделить K8: K11;

- через мастер функций f_x вызвать матричную операцию МУМНОЖ, в окне “Массив1” которой указать адрес исходной матрицы А – А8: D11, а в окне “Массив2” которой указать адрес полученного вектора решений X – J8: J11;

- затем одновременно нажать клавиши Ctrl-Shift-Enter.

В результате в ячейках K8: K11 появятся значения элементов вектора свободных членов B, рис. 6.2., совпадающие со значениями элементов исходного вектора B –F8: F11, а для любой ячейки диапазона K8: K11 в строке состояний подтверждение выполнения матричной операции {=МУМНОЖ(A8: D11; J8: J11)}.