💸 Как сделать бизнес проще, а карман толще?

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое раписание, но и напоминать клиентам о визитах тоже. Проблема в том, что средняя цена по рынку за такой сервис — 800 руб/мес или почти 15 000 руб за год. И это минимальный функционал. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!

Монохроматических световых полей

Пространственная когерентность

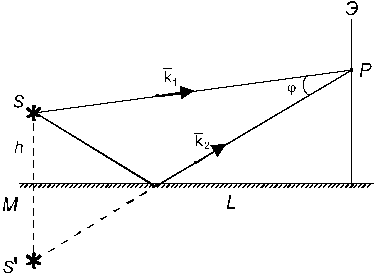Рис. 1. Схема опыта Ллойда.

Ухудшение видности интерференционной картины, связанное с конечными размерами источника, можно пояснить на примере опыта Ллойда (рис.1).

В опыте Ллойда когерентными являются источник S и его изображение S¢ в плоском зеркале М. Если точечный источник света излучает монохроматические волны длины l, то ширина интерференционной полосы (расстояние между точками экрана с максимальными I _max или минимальными I _min интенсивностями) определяется соотношением:

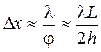, (1)

где j - угол между волновыми векторами и , h - расстояние от источника до поверхности зеркала, L - расстояние от источника до экрана.

Видность интерференционной полосы в этом случае (считаем, что когерентные источники одинаковы) равна 1.

Интервал длин волн, испускаемых реальным источником, будем считать малым для того, чтобы степень временной когерентности была достаточной для получения четкой интерференционной картины.

Отдельные участки протяженного источника света (например, S₁ и S₂ на рис.2) излучают волны, фазы которых не связаны между собой. Наблюдаемая на экране интерференционная картина в схеме Ллойда с таким источником, является наложением картин, создаваемых каждым участком в отдельности. Их нулевые максимумы (точки экрана, для которых разность хода лучей равна нулю) совпадают (точка О на рис.2).

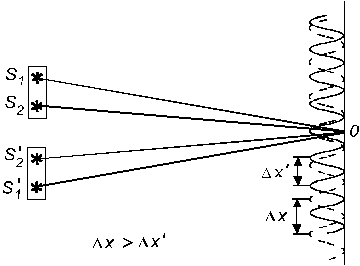Рис.2. Размывание интерференционных полос при использовании протяженного источника.

Поскольку ширины интерференционных полос 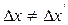(см. соотношение (1), в котором 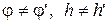), то видность V результирующей картины будет ухудшаться с возрастанием номера полосы.

Как видность V связана с размерами протяженного источника?

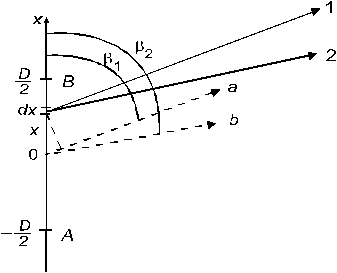Рис.3. К определению разности хода лучей 1 и 2.

Пусть имеется равномерно светящаяся щель АВ ширины D (рис.3), расположенная перпендикулярно плоскости рисунка.

Направим ось X вдоль АВ и поместим начало отсчета в середине АВ. Один элементарный источник ширины dx создает на экране интерференционную картину. Направление распространения лучей 1 и 2 зависит от выбора конкретной оптической схемы. Например в опыте Ллойда луч 1 непосредственно падает на экран Э (рис.1), а луч 2 - отражается от зеркала. Так как интенсивности пучков 1 и 2 одинаковы и равны (I₀ - интенсивность всего источника) распределение интенсивности в элементарной интерференционной картине будет следующим (см. соотношения (5) и (9) теоретического раздела):

, (2)

где D(x) - разность хода лучей 1 и 2 от данного элемента до точки наблюдения. Ее можно представить как:

, (3)

где D₀ - оптическая разность хода лучей a и b, вышедших из центра источника. Второе слагаемое в соотношении (3), дополнительная разность хода лучей 1 и 2 по отношению к лучам а и b, связано с конечным размером источника.

Найдем теперь распределение интенсивности в суммарной интерференционной картине:

, (4)

где .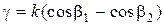

Интегрируем (4):

. (5)

Видность интерференционных полос будет равна (рис.4):

Рис.4. Зависимость видности V от линейных D или угловых qразмеров источника

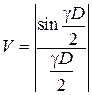. (6)

Применим полученный результат к расчету видности интерференционной картины в схеме Юнга (рис.5):

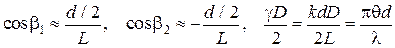, (7)

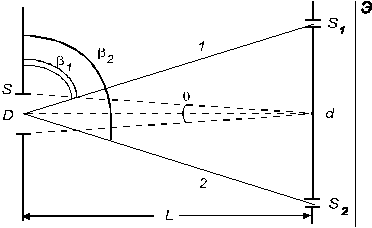Рис.5 Интерференционная схема Юнга.

где d - расстояние между щелями, q - угловой размер источника света (щель ширины D).

Окончательно, видность V равна:

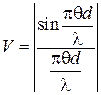. (8)

Видность интерференционных полос, полученных от щелей S ₁ и S ₂ , равна нулю, если 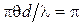, т.е. при выполнении условия:

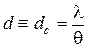(9)

Если поместить щели S ₁ и S ₂ на расстоянии d > d _c, то видность интерференционных полос будет очень мала (см. рис.4; d > d _c, соответствует значениям аргумента 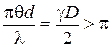), т.е. колебания в точках S ₁ и S ₂ будут некогерентными. Другими словами, колебания в двух точках волнового фронта, отстоящих от источника света на расстоянии L, будут когерентными, если расстояние между ними не превосходит d _c. Эту величину называют радиусом (областью) когерентности.

Таким образом, оказывается, что интерференционный опыт Юнга позволяет выяснить, насколько когерентны между собой колебания в поперечном сечении светового пучка, достигающего щелей S ₁ и S ₂. Варьируя расстояние между щелями S ₁ и S ₂ и одновременно измеряя видность интерференционной картины на расположенном за ними экране, можно «обследовать» когерентность колебаний по всей площади этого сечения.

Уменьшение видности интереференционной картины, обусловленное конечным размером источника, связывают с понятием пространственной когерентности. А для количественной характеристики когерентности колебаний в поперечном сечении пучка вводят понятие радиуса когерентности.

Лазерная спекл - структура

Когда наблюдатель рассматривает в лазерном свете диффузно отражающий или преломляющий объект, изображение кажется ему зернистым. Создается впечатление, что поверхность объекта покрыта множеством мелких, хаотически расположенных светлых и темных пятнышек - так называемых спеклов (от английского слова speckle - испещрять). Если наблюдатель смещается, то ему кажется, что спекл - структура мерцает и смещается относительно объекта. Явление возникновения спеклов связано с использованием высококогерентного света.

Физическая природа спеклов проста. Каждая точка объекта рассеивает некоторое количество света в направлении наблюдателя. Вследствие своей высокой когерентности лазерный свет, рассеянный одной из точек объекта, интерферирует со светом, рассеянным любой другой точкой объекта. Сетчатка глаза регистрирует картину хаотической интерференционной картины. Это и есть спеклы. Хаотичность обусловлена шероховатостью поверхности, так как фаза рассеянного света изменяется случайно от точки к точке, следуя за вариациями высоты рельефа в данном месте. Аналогично можно рассмотреть и возникновение спеклов на экране при прохождении лазерного света через матовую пластинку.

Вследствие нерегулярной толщины матовой пластинки пространственно когерентная лазерная волна приобретает приращение фазы, случайным образом изменяющееся от точки к точке поверхности пластинки. Свет, прошедший через матовую пластинку, хорошо моделирует излучение протяженного самосветящегося источника.

Важное отличие матового стекла от самосветящегося источника света состоит в следующем: фазовые соотношения между световыми колебаниями в разных точках матового стекла нерегулярны, но неизменны во времени. Поэтому зернистая структура освещенности экрана также постоянна во времени. В случае же самосветящегося источника разность фаз колебаний в двух каких - либо точках его поверхности будет быстро изменяться, что приведет, очевидно, к хаотическому движению зерен и исчезновению зернистой структуры. Можно сказать, что спекл - картина, наблюдаемая от матового стекла, отвечает мгновенному распределению освещенности, возникающему в случае самосветящегося источника.

Участки экрана с повышенным значением освещенности отвечают, очевидно, тому, что волны, приходящие в них из различных точек матового стекла, оказываются, по случайным обстоятельствам, преимущественно синфазными. Наоборот, в участках с пониженной освещенностью происходит взаимное гашение волн, приходящих из различных точек матового стекла. Для того, чтобы степень синфазности этих волн существенно изменилась, нужно сместиться в плоскости экрана на некоторое расстояние; его среднее значение и будет определять размер области когерентности. Таким образом, «среднее зерно» есть область когерентности, а средний его размер - радиус когерентности.

При движении матового стекла происходит случайное изменение во времени фаз интерферирующих волн. Результирующее поле сходно со световым полем самосветящегося источника. При этом: радиус когерентности у полученного светового поля не изменяется (он определяется угловым размером источника), а спекл - картина исчезает.