Квантовые состояния. Уравнение Шредингера

Уравнения Шредингера для микрочастицы, движущейся в потенциальной яме. Волновая функция и ее физический смысл. Энергия микрочастицы. Распределение плотности вероятности.

М. Борн (1882—1970) в 1926 г. предположил, что по волновому закону меняется не сама вероятность, а величина, названная амплитудой вероятности и обозначаемая Y(х, у, z, t). Эту величину называют также волновой функцией (или Y-функцией). Амплитуда вероятности может быть комплексной, и вероятность Wпропорциональна квадрату ее модуля:

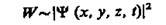
(|Y|² = YY*, Y * — функция, комплексно сопряженная с Y). Таким образом, описание состояния микрообъекта с помощью волновой функции имеет статистический, вероятностный характер: квадрат модуля волновой функции (квадрат модуля амплитуды волн де Бройля) определяет вероятность нахождения частицы в момент времени г в области с координатами хи x+dx, уи y+dy, zи z+dz.

Итак, в квантовой механике состояние микрочастиц описывается принципиально по-новому — с помощью волновой функции, которая является основным носителем информации об их корпускулярных и волновых свойствах. Вероятность нахождения частицы в элементе объемом dV равна

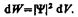
Величина

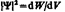
(квадрат модуля Y-функции) имеет смысл плотности вероятности, т. е. определяет вероятность нахождения частицы в единичном объеме в окрестности точки с координатами х, у, z. Таким образом, физический смысл имеет не сама Y-функция, а квадрат ее модуля |Y|², которым задается интенсивность волн де Бройля.

Вероятность найти частицу в момент времени е в конечном объеме V, согласно теореме сложения вероятностей, равна

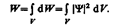
Основное уравнение нерелятивистской квантовой механики сформулировано в 1926 г. Э. Шредингером. Уравнение Шредингера, как и все основные уравнения физики (например, уравнения Ньютона в классической механике и уравнения Максвелла для электромагнитного поля), не выводится, а постулируется. Правильность этого уравнения подтверждается согласием с опытом получаемых с его помощью результатов, что, в свою очередь, придает ему характер закона природы. Уравнение Шредингера имеет вид

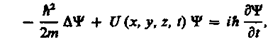(217.1)

где ℏ =h/(2p), т — масса частицы, D — оператор Лапласа

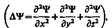
i — мнимая единица, U (х, у, z, f)— потенциальная функция частицы в силовом поле, в котором она движется, Y (х, у, z, t) — искомая волновая функция частицы.

Уравнение (217.1) справедливо для любой частицы (со спином, равным 0; см. § 225), движущейся с малой (по сравнению со скоростью света) скоростью, т. е. со скоростью v< < c. Оно дополняется условиями, накладываемыми на волновую функцию: 1) волновая функция должна быть конечной, однозначной и непрерывной (см. § 216); 2) производные 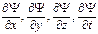должны быть непрерывны; 3) функция |Y| должна быть интегрируема; это условие в простейших случаях сводится к условию нормировки вероятностей (216.3).

Квантовые числа, их физический смысл

Квантовые числа. В квантовой механике доказывается, что уравнению Шредингера удовлетворяют собственные функции Y (r, в, < р), определяемые тремя квантовыми числами: главным л, орбитальным / и магнитным /и/.

Главное квантовое число л, согласно (223.3), определяет энергетические уровни электрона в атоме и может принимать любые целочисленные значения начиная с единицы:

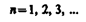
Из решения уравнения Шредингера вытекает, что момент импульса (механический орбитальный момент) электрона квантуется, т. е. не может быть произвольным, а принимает дискретные значения, определяемые формулой

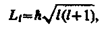
где l — орбитальное квантовое число, которое при заданном л принимает значения

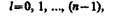
т. е. всего n значений, и определяет момент импульса электрона в атоме.

Из решения уравнений Шредингера следует также, что вектор L _l момента импульса электрона может иметь лишь такие ориентации в пространстве, при которых его проекция L _lx на направление z внешнего магнитного поля принимает квантованные значения, кратные n:

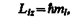
где m _l — магнитное квантовое число, которое при заданном l может принимать значения

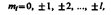
т. е. всего 2 l+ 1 значений. Таким образом, магнитное квантовое число m _l определяет проекцию момента импульса электрона на заданное направление, причем вектор момента импульса электрона в атоме может иметь в пространстве 2 l +1 ориентации.

Спин электрона (и всех других микрочастиц) — квантовая величина, у нее нет классического аналога; это внутреннее неотъемлемое свойство электрона, подобное его заряду и массе.

Если электрону приписывается собственный механический момент импульса (спин) L_s, то ему соответствует собственный магнитный момент p_ms. Согласно общим выводам квантовой механики, спин квантуется по закону

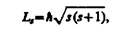
где s — спиновое квантовое число.

По аналогии с орбитальным моментом импульса, проекция L_aспина квантуется так, что вектор L, может принимать 2s + 1ориентации. Так как в опытах Штерна и Герлаха наблюдались только две ориентации, то 2s+1=2, откуда s = ½. Проекция спина на направление внешнего магнитного поля, являясь квантованной величиной, определяется выражением, аналогичным (223.6):

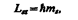
где m_s— магнитное спиновое квантовое число; оно может иметь только два значения:

m_s = ± 1/2

Стационарное уравнение Шредингера. Частица в одномерной потенциальной яме. Прохождение частицы через потенциальный барьер.

Уравнение 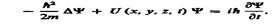является общим уравнением Шредннгера. Его также называют уравнением Шредингера, зависящим от времени. Для многих физических явлений, происходящих в микромире, уравнение (217.1) можно упростить, исключив зависимость Yот времени, иными словами, найти уравнение Шредингера для стационарных состояний — состояний с фиксированными значениями энергии. Это возможно, если силовое поле, в котором частила движется, стационарно, т. е. функция U = U(х, у, z)не зависит явно от времени и имеет смысл потенциальной энергии. В данном случае решение уравнения Шредингера может быть представлено в виде произведения двух функций, одна из которых есть функция только координат, другая — только времени, причем зависимость от времени выражается множителем 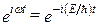, так что

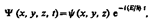
где Е— полная энергия частицы, постоянная в случае стационарного поля. Подставляя (217.4) в (217.1), получим

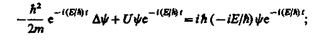
откуда после деления на общий множитель е и соответствующих преобразовании придем к уравнению, определяющему функцию y:

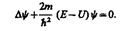
Уравнение называется уравнением Шредингера для стационарных состояний.

Проведем качественный анализ решений уравнения Шредингера применительно к частице в одномерной прямоугольной «потенциальной яме» с бесконечно высокими «стенками». Такая «яма» описывается потенциальной энергией вида (для простоты принимаем, что частица движется вдоль оси х)

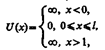
где l — ширина «ямы», а энергия отсчитывается от ее дна (рис. 296).

Уравнение Шредингера (217.5) для стационарных состояний в случае одномерной задачи запишется в виде

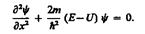
По условию задачи (бесконечно высокие «стенки»), частица не проникает за пределы «ямы», поэтому вероятность ее обнаружения (а следовательно, и волновая функция) за пределами «ямы» равна нулю. На границах «ямы» (при х = 0 и х = l)непрерывная волновая функция также должна обращаться в нуль. Следовательно, граничные условия в данном случае имеют вид

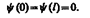
В пределах «ямы» (0 £ х £ l) уравнение Шредингера (220.1) сведется к уравнению
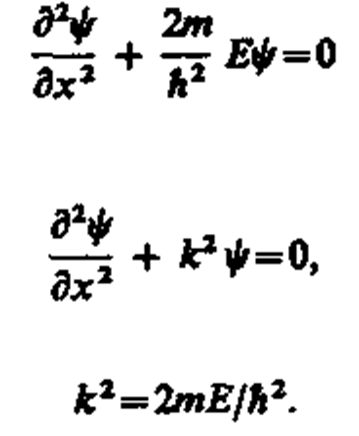