Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Молекулярные токи.

Всякое вещество является магнетиком, т.е. способно под действием магнитного поля приобретать магнитный момент (намагничиваться).

Намагниченное вещество создает магнитное поле , которое накладывается на обусловленное токами поле .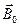

Результирующее поле, таким образом, равно: .

С точки зрения Ампера, намагничение тел объясняется наличием в молекулах циркулирующих токов, которые получили название молекулярных токов. Каждый такой ток обладает магнитным моментом и создает в окружающем пространстве магнитное поле. В отсутствие внешнего поля молекулярные токи ориентированы беспорядочным образом, и результирующее поле равно нулю.

Под действием магнитного поля магнитные моменты поворачиваются по полю и вследствие этого магнетик намагничивается, магнитный момент его становится отличным от нуля и возникает поле .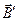

Намагниченностью 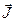называют магнитный момент единицы объема ,

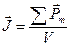где 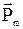– магнитный момент отдельной молекулы.

Поле 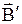также как и поле не имеет источников,

поэтому дивергенция результирующего поля равна нулю: .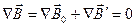

Вектор результирующего поля равен ,

причем, , где 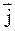– плотность макроскопического тока.

Тогда, по аналогии,

ротор вектора 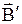должен быть пропорционален плотности молекулярных токов: ,

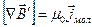а ротор результирующего поля равен: . (10)

Таким образом, для того, чтобы вычислить ротор 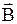, надо знать плотность как макротоков, так и молекулярных токов, причем плотность молекулярных токов зависит от .

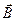Чтобы обойти это затруднение, необходимо ввести некоторую вспомогательную величину.

Найдем ее.

Выразим плотность молекулярных токов , через намагниченность магнетика .

Сумма молекулярных токов, охватываемых замкнутым контуром, равна интегралу по поверхности этого контура: .

(рис.9.). Рассмотрим элемент контура 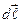, который образует с вектором намагниченности 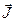угол

Этот элемент нанизывают на себя молекулярные токи, центры которых попадают внутрь косого цилиндра объемом 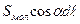(где –площадь, охватываемая отдельным моле- кулярным током).

Если число молекул в единице объема обозначить через n, то суммарный молекулярный ток, охватываемый элементом 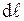, можно выразить формулой: .

Произведение 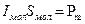– это магнитный момент отдельного молекулярного тока.

Тогда – магнитный момент единицы объема, по определению – это модуль вектора намагниченности .

.

Тогда 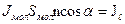- проекция вектора на направление .

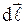Таким образом, суммарный молекулярный ток, охватываемый элементом 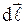, равен скалярному произведению 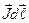, а сумма молекулярных токов, охватываемых всем контуром, равна: .

Правую часть этого выражения преобразуем по теореме Стокса: .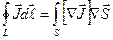

- циркуляция вектора 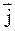по произвольному контуру L равна потоку вектора rotj через произвольную поверхность S, ограниченную данным контуром.

где S – поверхность, которая опирается на контур L,

получаем 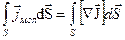- интегралы равны.

Это возможно, когда равны подинтегральные выражения.

Или 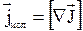(11)

- плотность молекулярных токов равна ротору вектора намагниченности.

Подставим значение из (11) в выражение (10), имеем: ,

или (12) .

Сравнив последнее выражение с законом полного тока в форме (4), видим, что разность векторов, стоящая под знаком ротора в левой части (12) есть не что иное,

как вектор напряженности : 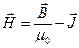- это и есть искомый вспомогательный вектор.

Вектор для магнитного поля является аналогом вектора электрического смещения для поля электрического. Он, также как и не зависит от среды.

Принято, что в каждой точке магнетика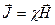

где 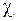– магнитная восприимчивость, характеризующая способность вещества намагничиваться.

В слабых полях 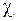не зависит от .

Тогда , или ,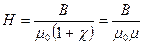

Причем 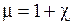– магнитная проницаемость вещества.