💸 Как сделать бизнес проще, а карман толще?

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое раписание, но и напоминать клиентам о визитах тоже. Проблема в том, что средняя цена по рынку за такой сервис — 800 руб/мес или почти 15 000 руб за год. И это минимальный функционал. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!

Расчет неразветвленной цепи переменного тока.

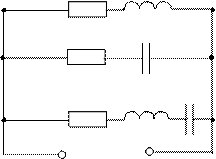
Цепь переменного тока содержит различные элементы (резисторы, катушки индуктивности, конденсаторы), включенные последовательно. Общий вид цепи показан на рисунке 1. В зависимости от данных нарисовать схему и определить следующие величины:

1) полное сопротивление цепи Z;

2) падение напряжения на каждом элементе и напряжение U, приложенное к цепи;

3) ток I в неразветвленной части цепи;

4) угол сдвига фаз (по величине и знаку);

5) активную, реактивную и полную мощности для всей цепи;

6) определить характер цепи.

Начертить в масштабе векторную диаграмму напряжений, треугольники сопротивлений и мощностей, и пояснить их построение.

R1 X_L1 R2 X_C1 R3 X_L2 X_C2

Рисунок 1.

Таблица №1.

Расчет разветвленной цепи переменного тока

методом проводимостей.

Разветвленная цепь переменного тока состоит из трех параллельных ветвей, содержащих различные элементы (резисторы, катушки индуктивности, конденсаторы). Общий вид цепи показан на рисунке 1. П Р И М Е Ч А Н И Е: Индекс «1» - у дополнительного параметра означает, что он относится к первой ветви; индекс «2» - ко второй, «3» - к третьей. В зависимости от данных нарисовать схему и определить следующие величины:

7) полные сопротивления ветвей Z₁, Z₂, Z₃;

8) активные и реактивные проводимости параллельных ветвей;

9) токи I₁, I₂, I₃ в ветвях;

10) ток I в неразветвленной части цепи;

11) угол сдвига фаз (по величине и знаку);

12) активную, реактивную и полную мощности для всей цепи.

Начертить в масштабе векторную диаграмму и пояснить ее построение.

R1 X_L1

R2 X_C2

R3 X_L3 X_C3

Рисунок 1.

Таблица №1.

Расчет трехфазной цепи.

1. В трехфазную четырехпроводную сеть с линейным напряжением U_л включили звездой разные по характеру сопротивления (рисунок 1). Определить фазное напряжение, активную, реактивную, полную мощности. Найти линейные токи и начертить в масштабе векторную диаграмму цепи. По векторной диаграмме определить числовое значение тока в нулевом проводе (задача для четных номеров).

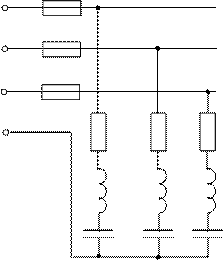А A

В B

С C

N R_A R_B R_C R_AB R_BC R_CA

X_LA X_LB X_LC X_LAB X_LBC X_LCA X_CA X_CB X_CC X_CAB X_CBC X_CCA

Рисунок 1. Рисунок 2.

2. В трехфазную сеть с линейным напряжением U_л включены треугольником разные по характеру сопротивления (рисунок 2). Определить фазные и линейные токи, активную, реактивную и полную мощности потребляемой всей цепью. Начертить векторную диаграмму цепи и по ней определить числовые значения линейных токов. (задача для нечетных номеров)

ПРИМЕЧАНИЕ. Все данные приведены в таблице №1. Схему рисовать исходя из данных.

Таблица 1.

1.6. Примеры решения типовых задач

Определить эквивалентное сопротивление цепи показанной на рис.1, если R₁=R₃=R₅=R₆=3 Ом, R₂=20 Ом, R₄=24 Ом. Найти силу тока идущего через каждый резистор, если к цепи приложено напряжение U=36В.

R1 R3

R2 R4

R6 R5

Рис. 1

1. Определяем эквивалентное сопротивление цепи R_эк. Сопротивления R₃, R₄, R₅ соединены последовательно

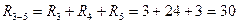Ом

2. Сопротивления R₂ и R_3-5 соединены параллельно, поэтому

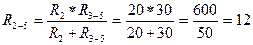Ом

3. Сопротивления R₁, R_2-5, R₆ соединены последовательно

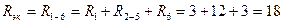Ом

4. Показываем на схеме токи, протекающие по каждому сопротивлению, и находим их. Так как напряжение U приложено ко всей цепи, то согласно закону Ом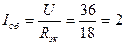а

А

5. Так как сопротивления R₁, R_2-5, R₆ соединены последовательно, то А

6. Найдем падения напряжения

Указания к решению задач 2 и 3.

Эти задачи относятся к разветвленным и неразветвленным переменного тока. Перед их решением изучите материал темы 3.1., ознакомьтесь с методикой построения векторных диаграмм.

Пример 2. Активное сопротивление катушки r_к=6 Ом, индуктивность ее L=0, 0318. Последовательно с катушкой включено активное сопротивление R=2 Ом и конденсатор емкостью С=795 мкФ. К цепи приложено напряжение U=100 В. Определить: полное сопротивление цепи, силу тока, коэффициент мощности, активную, реактивную и полную мощности, напряжения на каждом сопротивлении. Начертить в масштабе векторную диаграмму. Частота тока в цепи f=50 Гц.

r_k L R C

U

Рисунок 2

Решение:

1. Найдем индуктивное сопротивление катушки и емкостное сопротивление конденсатора

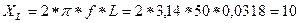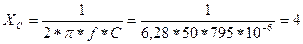Ом

Ом

2. Полное сопротивление цепи 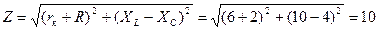Ом

3. Сила тока А

4. Коэффициент мощности , по таблице Брадиса находим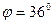

Определяя угол сдвига фаз через четную функцию косинус, мы теряем знак угла. Поэтому в тех случаях, где важен знак угла, следует пользоваться нечетными его функциями (синусом или тангенсом). В нашем примере

,

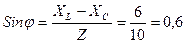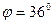
Знак плюс у угла показывает, что напряжение опережает ток.

5. Активная мощность 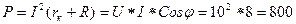Вт

6. Реактивная мощность 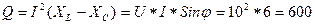Вар

7. Полная мощность 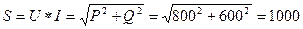ВА

8. Для построения векторной диаграммы найдем напряжения на сопротивлениях цепи

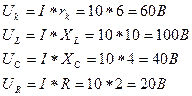
Построение векторной диаграммы начнем с выбора масштабов для тока и напряжения. Задаемся масштабом по току: в 1 См-4 А и масштабом по напряжению: в 1См – 20 В.

Построение векторной диаграммы начнем с вектора тока, который откладываем по горизонтали в масштабе

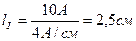
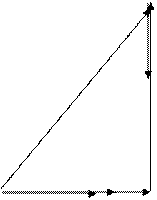U_C

U U_L

U_k U_R

I

Вдоль вектора тока откладываем напряжения на активных сопротивлениях r_k и R:

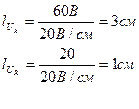
Из конца вектора U_R откладываем в сторону опережения (против часовой стрелки) вектора тока на 90⁰ вектор напряжения U_L на индуктивном сопротивлении. Длина вектора

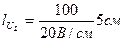
Из конца вектора U_L откладываем в сторону отставания от вектора тока на 90⁰ вектор напряжения на емкостном сопротивлении U_C. Длина вектора

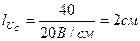
Геометрическая сумма векторов U_k, U_R, U_L, U_C представляет полное напряжение U. Так как длина вектора равна 5 см, то величина напряжения составит

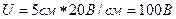
Пример 3. Катушка с активным сопротивлением r=20 Ом и индуктивным сопротивлением X_L= 15 Ом, соединена параллельно с конденсатором, емкостное сопротивление которого X_C=50 Ом. Определить токи в ветвях и в неразветвленной части цепи, активные и реактивные мощности ветвей и всей цепи; начертить в масштабе векторную диаграмму. К цепи приложено напряжение U=100 В.

R X_L

X_C

U

Рисунок 3

Решение:

1. Найдем токи в ветвях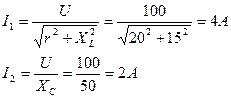

2. Углы сдвига фаз будем находить по синусам во избежание потери знаков углов: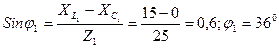

(φ ₁> 0, т.е. напряжение опережает ток)

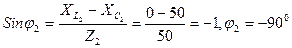
(φ ₂< 0, т.е. напряжение опережает ток)

3. Активные и реактивные составляющие токов ветвей:

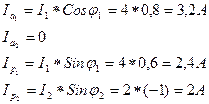
4. Ток в неразветвленной части цепи

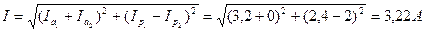
5. Коэффициент мощности всей цепи

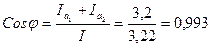
6. Активные мощности ветвей и всей цепи:

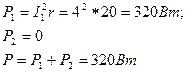
7. Реактивные мощности ветвей и всей цепи:

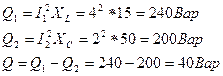
8. Полная мощность цепи:

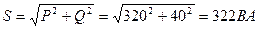
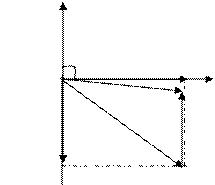
I_р2=I₂

I_а1 U

I

I_р1

I₁

9. Для построения векторной диаграммы задаемся масштабами: по току в 1 см-1 А; по напряжению в 1 см-25 В. Построение начнем с вектора напряжения U. Под углом φ ₁ к нему откладываем (в сторону отставания) в принятом масштабе вектор тока I₁; под углом φ ₂ (в сторону опережения) – вектор тока I₂. Геометрическая сумма этих векторов представляет ток I в неразветвленной части цепи. Проекции токов ветвей на вектор напряжения являются активными составляющими I_а1 и I_а2; проекция этих токов на вектор, перпендикулярный вектору напряжения, - реактивными составляющими I_р1 и I_р2.

Указания к решению задач 4 и 5

Решение этой группы задач требует знания учебного материала темы 3.2. «Трехфазные электрические цепи синусоидального переменного тока»; отчетливого представления об особенностях соединения потребителей в звезду и треугольник, соотношениях между линейными и фазными величинами при таких соединениях, а также умения строить векторную диаграмму при симметричной и несимметричной нагрузках.