💸 Как сделать бизнес проще, а карман толще?

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое раписание, но и напоминать клиентам о визитах тоже. Проблема в том, что средняя цена по рынку за такой сервис — 800 руб/мес или почти 15 000 руб за год. И это минимальный функционал. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!

Математический анализ

Одна из главных заслуг Эйлера перед наукой — монография «Введение в анализ бесконечно малых» (1748). В 1755 году выходит дополненное «Дифференциальное исчисление», а в 1768—1770 годах — три тома «Интегрального исчисления». В совокупности это фундаментальный, хорошо иллюстрированный примерами курс, с продуманной терминологией и символикой, откуда многое перешло и в современные учебники. Собственно современные методы дифференцирования и интегрирования были опубликованы в данных трудах.

Основание натуральных логарифмов было известно ещё со времён Непера и Якоба Бернулли, однако Эйлер выполнил настолько глубокое исследование этой важнейшей константы, что с тех пор она носит его имя. Другая исследованная им константа: постоянная Эйлера — Маскерони.

Первая книга по вариационному исчислению

Он делит с Лагранжем честь открытия вариационного исчисления, выписав уравнения Эйлера — Лагранжа для общей вариационной задачи. В 1744 году Эйлер опубликовал первую книгу по вариационному исчислению («Метод нахождения кривых, обладающих свойствами максимума либо минимума»).

Эйлер значительно продвинул теорию рядов и распространил её на комплексную область, получив при этом знаменитую формулу Эйлера. Большое впечатление на математический мир произвели ряды, впервые просуммированные Эйлером, в том числе не поддававшийся до него никому ряд обратных квадратов:

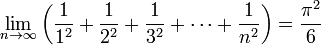
Современное определение показательной, логарифмической и тригонометрических функций — тоже его заслуга, так же, как и их символика и обобщение на комплексный случай^[20]. Формулы, часто именуемые в учебниках «условия Коши — Римана», более правильно было бы назвать «условиями Даламбера — Эйлера».

Он первый дал систематическую теорию интегрирования и используемых там технических приёмов, нашёл важные классы интегрируемых дифференциальных уравнений. Он открыл эйлеровы интегралы — ценные классы специальных функций, возникающие при интегрировании: бета-функция и гамма-функция Эйлера. Одновременно с Клеро вывел условия интегрируемости линейных дифференциальных форм от двух или трёх переменных (1739). Первый ввёл двойные интегралы. Получил серьёзные результаты в теории эллиптических функций, в том числе первые теоремы сложения.

С более поздней точки зрения, действия Эйлера с бесконечными рядами не всегда могут считаться корректными (обоснование анализа было проведено лишь полвека спустя), но феноменальная математическая интуиция практически всегда подсказывала ему правильный результат. Впрочем, дело было не только в интуиции, Эйлер действовал здесь достаточно сознательно, во многих важных отношениях его понимание смысла расходящихся рядов и операций с ними превзошло стандартное понимание XIX века и послужило основой современной теории расходящихся рядов, развитой в конце XIX — начале XX века^[21].