
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Погрешности измерений и оценка их характеристик
|
|
Вопрос № Случайные погрешности (ошибки)
Случайными являются такие ошибки, которые меняются непредсказуемо от одного измерения к другому при определении одной и той же физической величины с помощью одной и той же измерительной системы при неизменных условиях. Обычно они обусловлены большим числом факторов, которые влияют на результат измерения независимо. Мы не можем скорректировать случайные ошибки, так как нам неизвестны их причины и следствием их являются случайные (непредсказуемые) колебания результата измерения.
Примерами случайных ошибок служат:
ошибки наблюдателя;
ошибки регулировки и настройки Ипри;
ошибки округления и т. д.
Все, о чем мы можем говорить, имея дело со случайными ошибками, это вероятность того, что ошибка будет той или иной величины. Теория вероятностей и мат. статистика дают возможность делать определенные утверждения при наличии случайных ошибок.
Можно считать, что как систематические, так и случайные ошибки вызываются сигналом помехи, который накладывается на истинный сигнал при его измерении. Флюктуация помехи вызывает случайную ошибку, а постоянный сигнал помехи является причиной систематической погрешности. К сожалению, постоянный характер помехи делает задачу обнаружения систематических ошибок более трудной.
Влияние случайных ошибок можно уменьшить, осуществляя измерения несколько раз и принимая в качестве конечного результата среднее значение результатов отдельных измерений. Возможно это тогда, когда измеряемая величина не изменяется на протяжении всех этих измерений и измерения выполняются быстро. Среднее значение 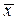 результатов
результатов 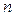 измерений
измерений 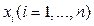 имеет вид:
имеет вид:
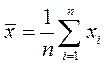 .
.
Среднее 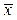 представляет собой лучшую возможную оценку значения
представляет собой лучшую возможную оценку значения 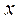 постоянной ФВ по
постоянной ФВ по 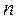 результатам измерений. Такой вывод можно сделать из того факта, что
результатам измерений. Такой вывод можно сделать из того факта, что
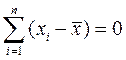
Таким образом, сумма всех отклонений 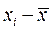 равна нулю. Кроме того, величина
равна нулю. Кроме того, величина
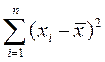
минимальна.
Другими словами, минимальными являются рассеяние 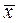 или разброс выборочных значений
или разброс выборочных значений  относительно среднего
относительно среднего 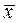 .
.
Мерой рассеяния 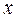 в окрестности среднего
в окрестности среднего 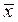 является дисперсия
является дисперсия  (мера концентрированности распределения), равная по определению,
(мера концентрированности распределения), равная по определению,
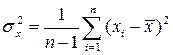 .
.
Обычно указывается квадратный корень из дисперсии; эта величина называется среднеквадратическим отклонением 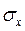 . Выборки
. Выборки 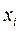 , полученные в отдельных измерениях величины
, полученные в отдельных измерениях величины 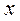 , при наличии случайный ошибок, можно представить на диаграмме в виде столбцов. Чтобы построить такую диаграмму, нам следует разбить диапазон всех возможных значений
, при наличии случайный ошибок, можно представить на диаграмме в виде столбцов. Чтобы построить такую диаграмму, нам следует разбить диапазон всех возможных значений 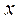
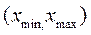 , включающий все выборки
, включающий все выборки  полученные в измерениях, на небольшие интервалы ширины
полученные в измерениях, на небольшие интервалы ширины 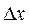 , а затем отложить число выборок
, а затем отложить число выборок 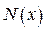 , попавших в эти небольшие интервалы
, попавших в эти небольшие интервалы 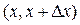 , как функцию от
, как функцию от 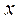 (см рис.1). Обычно размер мелких интервалов выбирается по правилу
(см рис.1). Обычно размер мелких интервалов выбирается по правилу
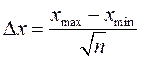 .
.
Если 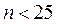 , то лучшее определить значение
, то лучшее определить значение  по правилу Старджеса
по правилу Старджеса
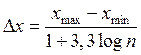 .
.
Если ширину интервала 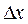 выбрать слишком малой, то «огибающая» диаграммы будет сильно изрезанной. При слишком большом значении
выбрать слишком малой, то «огибающая» диаграммы будет сильно изрезанной. При слишком большом значении 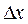 «огибающая» оказывается квантованной слишком грубо, и форма распределения проступает не так явно.
«огибающая» оказывается квантованной слишком грубо, и форма распределения проступает не так явно.
Можно построить нормализованную диаграмму, откладывая 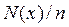 , а не
, а не 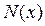 . Тогда по вертикали указывается относительное число измерений, результаты которых лежат в данном интервале. В этом случае можно утверждать, что теперь по оси ординат отложена вероятность попадания результата измерения в данный интервал. Кроме того, можно произвести нормализацию также и по ширине интервала
. Тогда по вертикали указывается относительное число измерений, результаты которых лежат в данном интервале. В этом случае можно утверждать, что теперь по оси ординат отложена вероятность попадания результата измерения в данный интервал. Кроме того, можно произвести нормализацию также и по ширине интервала 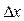 , откладывая
, откладывая 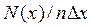 вместо
вместо 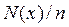 . Диаграмму, получающуюся в результате нормализации, обычно называют гистограммой.
. Диаграмму, получающуюся в результате нормализации, обычно называют гистограммой.
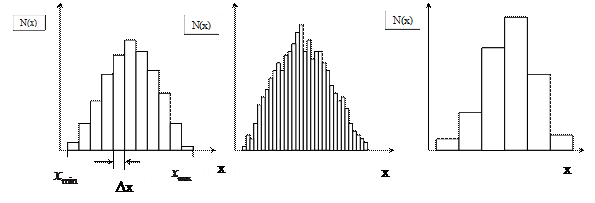 |
Рис.1 Гистограммы:
а. при правильном выборе ширины интервалов Δ х, на которые разбивается весь диапазон возможных значений х;
b. при слишком малых значениях Δ х;
c. при слишком больших значениях Δ х.
Если число выборок растет, а диапазон 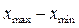 остается в ограниченных пределах, как это бывает на практике при измерении всех физических величин, то число интервалов, на которые разбивается этот диапазон, и число столбцов в гистограмме, увеличиваются, тогда как ширина одного интервала
остается в ограниченных пределах, как это бывает на практике при измерении всех физических величин, то число интервалов, на которые разбивается этот диапазон, и число столбцов в гистограмме, увеличиваются, тогда как ширина одного интервала 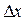 уменьшается. При
уменьшается. При 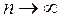 огибающая гистограммы переходит в гладкую кривую. Такая (дважды) нормализованная гистограмма носит название плотности распределения вероятностей
огибающая гистограммы переходит в гладкую кривую. Такая (дважды) нормализованная гистограмма носит название плотности распределения вероятностей 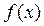 . По определению,
. По определению,
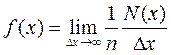 .
.
Это соотношение можно также записать в виде:
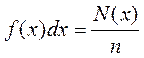 .
.
Это означает, что 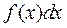 есть вероятность того, что значение выборки попадает в интервал между
есть вероятность того, что значение выборки попадает в интервал между 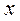 и
и 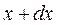 ; отсюда и следует название: плотность распределения вероятности. Из последнего равенства следует, что
; отсюда и следует название: плотность распределения вероятности. Из последнего равенства следует, что
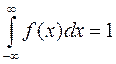 .
.
Интеграл в этом выражении представляет собой сумму всех вероятностей 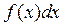 . Он равен вероятности того, что очередная выборка попадет в первый интервал ширины
. Он равен вероятности того, что очередная выборка попадет в первый интервал ширины 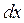 , или во второй, или в третий и т.д. Так как результат измерения должен принадлежать одному из этих интервалов, сумма должна равняться 1. Последнее соотношение показывает, что единице равна площадь под плотностью распределения вероятностей (что и достигается, главным образом, путем двукратной нормализации). Зная плотность распределения вероятностей, легко найти вероятность того, что результат очередного измерения окажется меньше определенного значения а (см. рис.2). Обозначая эту вероятность
, или во второй, или в третий и т.д. Так как результат измерения должен принадлежать одному из этих интервалов, сумма должна равняться 1. Последнее соотношение показывает, что единице равна площадь под плотностью распределения вероятностей (что и достигается, главным образом, путем двукратной нормализации). Зная плотность распределения вероятностей, легко найти вероятность того, что результат очередного измерения окажется меньше определенного значения а (см. рис.2). Обозначая эту вероятность 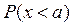 , получим
, получим
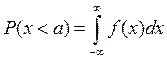
Эта величина в точности равна площади под 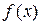 слева от линии х = а (см. рис.2).
слева от линии х = а (см. рис.2).
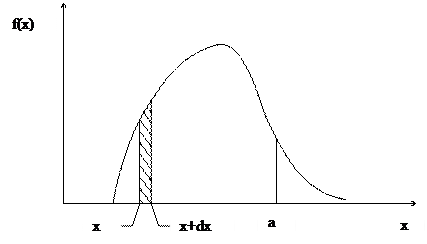 |
Рис.2 Плотность распределения вероятностей.
Точно так же при заданной плотности распределения 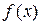 можно найти среднее
можно найти среднее 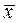 набора выборочных значений
набора выборочных значений 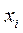 :
:
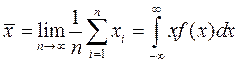 .
.
Дисперсию можно представить в виде:
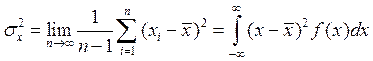 .
.
Отметим ещё раз, что СКО – это квадратный корень из дисперсии:
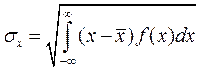
Если ошибки, содержащиеся в результатах измерений, обусловлены большим числом взаимно независимых событий, то можно доказать, что они распределены по вполне определенному закону: в этом случае распределение вероятностей является нормальным или гауссовым. Доказательство содержится в центральной предельной теореме теории вероятностей.
Плотность вероятности нормального распределения имеет вид:
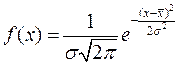 ;
;
график такого распределения показан на рис.3. Вероятности того, что 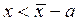 или
или 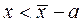 , выражаются следующими интегралами, соответственно:
, выражаются следующими интегралами, соответственно:
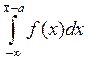
и
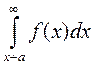 ;
;
эти интегралы нельзя представить с помощью элементарных функций.
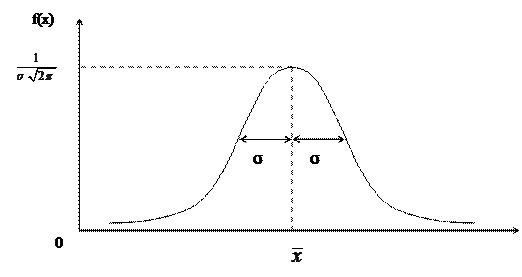 |
Рис.3 Нормальное или гауссово распределение
Примеры найденных численно приближенных значений этих интегралов представлены в табл.1. «Вероятность того, что результат измерения, имеющий нормальное распределение со средним значением и СКО, лежит вне интервалов шириной 1 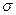 , 2
, 2 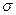 и 3
и 3 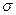 с центром в точке
с центром в точке 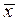 ».
».
Табл.1
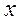 находится вне интервала находится вне интервала
| Вероятность |
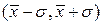
| 0, 32 |
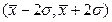
| 0, 045 |
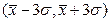
| 0, 0026 |
На рис.4 показан случай, когда результаты измерений содержат как случайные, так и систематические ошибки. Здесь случайные ошибки распределены по нормальному закону.
Истинное значение измеряемой величины равно а. Систематическая ошибка вызывает сдвиг среднего значения выборок, которое равно b. Полная ошибка (при верояности больших уклонений 0, 14%) равна сумме систематической ошибки а-b и «максимальной случайной ошибки». Этой полной ошибкой определяется погрешность измерения. Неопределенность результата измерения является мера разброса между выборками, обусловленного только случайными ошибками. Строго говоря, неопределенность результата измерения задается интервалом, в пределах которого истинное значение измеряемой величины находится с заданной доверительной вероятностью.
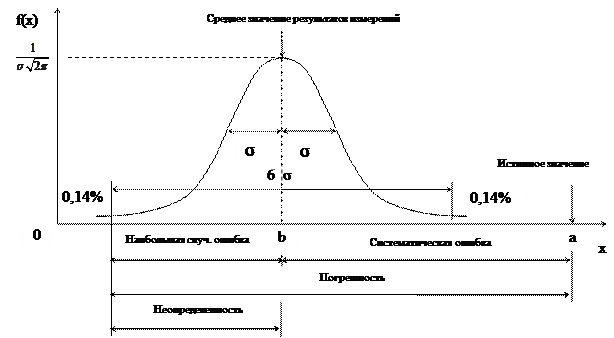 |
Рис.4 Случайные и систематические ошибки
|
|