
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение текстовых задач геометрическим методом.
|
|
В вузовском курсе математики у будущего учителя начальных классов, как правило, формируются умения решать задачи арифметическим и алгебраическим методами. Геометрический метод в явном виде не изучается, хотя и используется для построения вспомогательных моделей при решении задач различных видов (" на движение", " на работу", " на переливание" и т.д.). В начальном курсе математики для облегчения решения многих текстовых задач также используются вспомогательные модели, имеющие ярко выраженную геометрическую окраску.
Геометрический метод решения текстовых задач базируется на основных понятиях планиметрии (точка, отрезок, длина, площадь, треугольник, прямоугольник и др.), а также свойствах плоских фигур и графиков элементарных функций. Математическая модель задачи в этом случае представляет собой либо диаграмму, либо график. Решить задачу геометрическим методом это значит найти ответ на требование задачи, используя геометрические построения или свойства геометрических фигур. Причем одну и ту же задачу можно решить различными геометрическими способами (Задача считается решенной различными способами, если для ее решения используются различные построения или свойства фигур).
Различаются два приема решения задач с использованием данного метода: конструктивный (чисто графический) и вычислительный (графико-вычислительный). При решении задачи конструктивным приемом диаграмма или график вычерчиваются как можно более точно, непосредственно по значениям величин, входящим в условие задачи. Построения делаются циркулем, линейкой, угольником на миллиметровой бумаге или бумаге " в клеточку". Ответ получается обычно приближенный, но приемлемый для практических целей: он находится при помощи измерений длин отрезков или других элементов чертежа, а зачастую просто " считывается" с чертежа. В том случае, когда используется вычислительный прием, диаграмма или график применяется как условное изображение связи между рассматриваемыми величинами. Чертеж, как правило, выполняется от руки - в виде наброска, эскиза. Решение задачи осуществляется аналитически, путем вычислений, но основывается на точных геометрических соотношениях.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Пример 1. Решим задачу " В одной канистре 2 литра воды, в другой - 6 л. Каждый час в первую доливают 3 литра воды, а во вторую - 2 литра. Через сколько часов в канистрах будет одинаковое количество воды? ", используя конструктивный прием.
Решение. Первый способ. Пусть 2 литра - это длина одного отрезка по вертикали, 1 час - это длина одного отрезка по горизонтали (рис. 1). Сначала откладываем отрезки, характеризующие первоначальное количество воды в каждой канистре, а затем отрезки, характеризующие количество воды, которая находится в каждой канистре к концу первого часа, затем - второго часа, третьего часа и наконец четвертого часа. Видим, что через 4 часа после начала наполнения в канистрах будет одинаковое количество вода.

|
Второй способ. Каждый час в канистру доливают одинаковое количество воды, поэтому количество воды, находящееся в каждой канистре, линейно зависит от времени. Отложим на оси Ох время (в часах), на оси Оу - количество воды (в литрах). Построим графики, характеризующие количество воды в каждой канистре (рис. 2) Абсцисса точки их пересечения (точки 0) указывает, через сколько часов в канистрах будет одинаковое количество воды Из чертежа видно, что ее значение равно 4. Ордината указывает, какое количество воды находится в канистрах. Ее значение равно 14.
Ответ: одинаковое количество воды в канистрах будет через 4 часа.
Пример 2. Решим задачу " Расстояние от города А до города В мотоциклист проехал за 4 часа. Если бы его скорость была на 20 км/ч меньше, то он проехал это расстояние за 5 часов. Определить расстояние между городами и скорость мотоциклиста, используя вычислительный и конструктивный приемы.
Решение. Вычислительный прием. Пусть в первом случае, предусмотренном условием задачи, время движения мотоциклиста (4 часа) изображается отрезком ОТ1, а скорость (ее величина пока еще неизвестна) - отрезком ОS1 (рис. 3). Тогда площадь прямоугольника ОS1O1T1 соответствует расстоянию между городами А и В. Пусть во втором случае скорость мотоциклиста изображается отрезком OS2, а соответствующее время (5 часов) - отрезком ОT2 В этом случае то же расстояние между городами А и В определяется площадью прямоугольника OS2O2Т2, равновеликого прямоугольнику OS1O1T1 Прямоугольник OS2O3T1 - общая часть прямоугольников ОS1O1T1 и OS2O2T2, поэтому равновеликими будут прямоугольники S2S1O1O3 и T1T2O2O3- Значит, S2S1*S2O3 = T1T2*T1O3- Учитывая, что S2S1 = 20 км/ч, S2O3 = 4 ч, T1T2 = 1 ч, находим T1O3 = (S2S1*S2O3)/T1O3 = (20 км/ч * 4ч)/1 ч = 80 км/ч. Следовательно, OS2 =T1O3=80км/ч, OS1= 80км/ч + 20км/ч = 100 км/ч, а расстояние между городами равно 100км/ч * 4ч = 400 км.
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
Геометрический метод достаточно редко используется как самостоятельный для решения текстовых задач, хотя некоторые задачи значительно проще решаются именно им.
 |

 S1 O1
S1 O1

 S2 O2
S2 O2
O3
 О
О
T1 T2
Пример 3. Решим задачу " Один завод может справиться с заданием за 20 дней. Через 10 дней после начала работы ему начинает помогать второй завод, который может справиться с этим заданием за 30 дней. Через сколько дней задание будет выполнено? "
рифметический метод. Примем все задание за 1.
1)1: 20 - 1/20 (ч.) - задания выполняет первый завод в день;
2)1: 30 = 1/30 (ч.) - задания выполняет второй завод в 1 день
3)1/20 х 10 = 1/2 (ч.) - выполняет завод за 10 дней;
4)1/20 + 1/30 - 5/60 (ч.) - оба завода выполнят в день, работая вместе;
5)1 - 1/2 = 1/2 (ч.) - осталось выполнить двум заводам;
6)1/2: 5/60 = 6 (д.) - за столько дней выполнят два завода оставшуюся часть задания;
7)10 + 6 = 16 (д.) - потребуется на выполнение всего задания.
Геометрический метод.
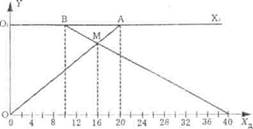
Построим графики выполнения задания каждым заводом. Отложим на оси 0Х время (в днях), на оси 0 - соответствующий объем задания, который будет выполнен заводом (рис. 4). Это количество будем измерять в частях всего задания: отрезок 001 условно обозначает этот объем (при арифметическом решении пишут: " Примем все задания за 1"). Для удобства проведем еще одну ось времени 0: хг. Отметим на верхней оси точку А (20 дней): тогда отрезок 0А - график выполнения задания первым заводом. Отметим на оси 0^ точку В (10 дней), а на 0х - точку С (ЗОд. + 10д. = 40д.); значит, отрезок ВС - график выполнения задания вторым заводом. Абсцисса точки пересечения этих графиков (точка М) указывает, через сколько дней после начала работы первого завода будет выполнено все задание. Из чертежа видно, что ее значение равно 16.
Ответ: все задание будет выполнено за 16 дней.
В некоторых случаях графическое решение задачи позволяет наглядно увидеть несоответствие между ответом и условиями задачи. Пример 4. Решим задачу " Школьники 4-го класса должны посадить 88 деревьев, школьники 3-го класса -76 деревьев. Ежечасно четвероклассники сажают 15 деревьев, а третьеклассники - 13 деревьев. Через сколько часов школьникам обоих классов останется посадить одинаковое количество деревьев?
Решение.
1) 88 - 76 = 12 (д.) _ на столько больше деревьев должны посадить четвероклассники, чем третьеклассники.
2)15 - 13 = 2 (д.) - на столько больше деревьев сажают каждый час четвероклассники, чем третьеклассники.
3) 12: 2 = б (ч) - через сколько часов школьникам обоих классов останется посадить одинаковое количество деревьев.
Рассуждения при решении данной задачи логичны и как будто бы правильные, но число, полученное в результате, не соответствует действительности. Если каждый час четвероклассники будут сажать по 15 деревьев, то через 6 часов они должны посадить 90 деревьев, а у них всего 88 деревьев. При графическом оформлении решения задачи несоответствия подобного рода между ответом и действительностью становятся наглядными и следовательно, заметными еще в процессе решения или даже в самом начале решения.
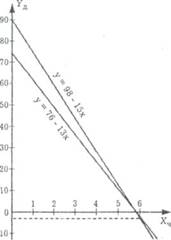
Приведем решение данной задачи геометрическим методом, используя конструктивный прием. Каждый час школьники сажают одинаковое количество деревьев, поэтому количество оставшихся деревьев линейно зависит о времени. Отложим на Рис. 4 оси 0Х время (в часах), па оси 0,. - количество деревьев. Построим графики, характеризующие количество деревьев, имеющихся у школьников каждого класса (рис. 5). Абсцисса точки их пересечения (точки 0) указывает, через сколько часов у школьников останется.
одинаковое количество деревьев. Из чертежа видно, что ее значение равно 6. Ордината указывает, какое количество деревьев осталось у школьников. Она отрицательна. Следовательно, все деревья школьники посадят раньше, чем наступит тот час, когда их могло бы остаться поровну.
|
Ответ: одинаковое количество деревьев у школьников остаться не может.
Чаще всего геометрический метод все же является вспомогательным при решении задач арифметическим или алгебраическим методами. Его используют при анализе задачи для построения ее графической модели, которая, в свою очередь, помогает найти путь решения задачи.
Пример 5.
Задача. В автобусе на 48 пассажиров больше, чем в троллейбусе. Сколько пассажиров находится в автобусе и троллейбусе отдельно, если в троллейбусе в четыре раза меньше, чем в автобусе?
Решение. Графическая модель задачи представлена на рис. 6 и " подсказывает" следующий путь решения задачи. Число пассажиров - в троллейбусе приеме за 1 часть. Тогда можно найти, сколько частей приходится на число пассажиров в автобусе, а затем, сколько частей приходится на 48 пассажиров. После этого можно определить число пассажиров составляющих 1 часть (находящихся в троллейбусе). Зная, что в автобусе пассажиров в четыре раза больше, найдем их число.
 | |
 |
?
 48 ч.
48 ч.
 | |
 |
?
1)1x4 = 4 (ч.) - приходится на пассажиров в автобусе;
2)4 - 1 = 3 (ч.) - приходится на разность между пассажирами в автобусе и троллейбусе,
3)48: 3 = 16 (пас.) - в троллейбусе;
4)16 х 4 = 64 (пас.) - в автобусе.
Ответ: в автобусе 64 пассажира, в троллейбусе 16 пассажиров.
Рассмотренные примеры показывают, что геометрический метод решения текстовых задач во многих случаях облегчает поиск пути решения задачи, упрощает ее решение, позволяет проверить правильность полученного ответа. В процессе математической подготовки будущего учителя начальных классов необходимо помочь студентам усвоить сущность этого метода и научить применять его при решении задач.
|
|
