Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Ход работы. По специальным главам информатики

ЛАБОРАТОРНАЯ РАБОТА №1

По специальным главам информатики

Решение дифференциального уравнения методом Эйлера

Автор отчета (подпись) 09.01.2012 Бобков А.В.

Обозначение отчета ЛР-02069964-210700-03-12

Преподаватель (подпись) 09.01.2012 Маняев И.В.

Саранск 2012

Краткая теория

Метод Эйлера.

Решить дифференциальное уравнение у/=f(x, y) численным методом - это

значит для заданной последовательности аргументов х0, х1…, хn и числа у0, не определяя функцию у=F(x), найти такие значения у1, у2, …, уn, что уi=F(xi)(i=1, 2, …, n) и F(x0)=y0. Таким образом, численные методы позволяют вместо нахождения функции У=F(x) получить таблицу значений этой функции для заданной

последовательности аргументов. Величина h=xk-xk-1 называется шагом

интегрирования.

Метод Эйлера относиться к численным методам, дающим решение в виде

таблицы приближенных значений искомой функции у(х). Он является

сравнительно грубым и применяется в основном для ориентировочных расчетов. Однако идеи, положенные в основу метода Эйлера, являются исходными для ряда других методов.

Формула метода Эйлера.

y_i=y_i-1+h*f(x_i-1; y_i-1)

где h-шаг.

Ход работы

1. Составим алгоритм программы для решения дифференциального уравнения dy/dx=2*(x^2+y), y(0)=1 на отрезке [0; 1] с шагом h=0.1;

Листинг 1.код решения дифференциального уравнения методом Эйлера

Program zadanieeil1;

Var

m, z, d, h, x, y: real; {m-начальное значение х, d-значение у при х=0, z-переменная необходимая для выхода из программы}

i: integer;

Function f(x, y: real): real;

Begin

end;

Begin

Writeln(Полученные значения ');

Writeln(' dy/dx=2*(x^2+y) ');

m: =0; d: =1; z: =1; h: =0.1; {присвоение начальных значений значений }

Writeln('--------------------');

Writeln('| i | x | y |');

Writeln('--------------------');

x: =m; y: =d; i: =1;

Writeln('|', i: 2, ' |', x: 5: 2, ' |', y: 7: 4, ' |');

repeat

y: =y+h*f(x, y);

Writeln('|', i: 2, ' |', x: 5: 2, ' |', y: 7: 4, ' |');

x: =x+h;

i: =i+1;

until x> z;

Writeln('--------------------');

Readln;

End.

Полученный результат

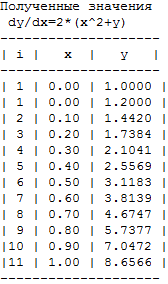
Рисунок 1-полученные значения х и у

2.Составим Блок-схему алгоритма программы решения дифференциального уравнения методом Эйлера.

Рисунок 2-Блок-схема алгоритма

Вывод: Изучен метод Эйлера для решения дифференциальных уравнений.