
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Круговое движение.
|
|
Задача этого раздела – убедить вас, что круговое движение с постоянной скоростью на самом деле является ускоренным движением под действием силы, направленной к центру круга. Этот результат был ещё одним мало отмеченным вкладом Гюйгенса, однако Ньютон, видимо, получил его независимо некоторое время спустя.
Начнём аргументацию с обращения к вашей интуиции о том, что для изменения направления движения объекта необходима некая сила, направление которой не совпадает с направлением движения. Следующим шагом следует показать, что именно такая сила появляется, когда объект движется по кругу. Затем мы докажем сходство между круговым движением и более привычными формами ускоренного движения. Наконец, мы получим формулу для такого ускорения.
Представьте себе большой тяжёлый шар, который медленно катится по ровному полу. Если, находясь сзади него, мы толкаем его по направлению движения, то он ускорится. Аналогично, если мы находимся перед шаром и толкаем его в направлении, противоположном движению, шар замедлится.
Чтобы изменить направление движения шара, нужен толчок сбоку. Если этот толчок, в итоге, направлен по движению, шар ускорится и, вместе с тем, изменит направление движения. Если же толчок, в целом, произведён из положения перед шаром, он замедлится. Только толчок под прямым углом к направлению движения может изменить направление движения без изменения скорости.
Теперь привяжем к шару (всё ещё на полу) верёвку, другой конец которой закреплён на полу гвоздём. Шар будет двигаться по кругу. Конечно, в этом случае на шар действует вынуждающая сила: верёвка натянута, а гвоздь прочно вбит в пол. Шар может двигаться только в направлении, перпендикулярном верёвке, находясь на постоянном расстоянии от гвоздя. Верёвка может тянуть шар только в направлении к гвоздю. Если мы не будем учитывать трение и вызванное им замедление шара, то натяжение верёвки, будет оставаться постоянным. Итак, сила, действующая на шар, постоянна по величине, но непрерывно изменяет своё направление, всегда указывая на центр круга.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
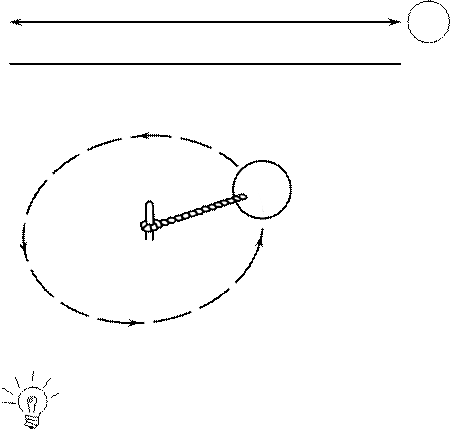
Предположим теперь, что мы поместили на полу на большом расстоянии от круга яркий источник света, и наблюдаем тень от шара на противоположной стене, как это показано на рис. 3 - 1. Тень движется «туда-сюда», как маятник, постоянно замедляясь, меняя направление движения на обратное, и снова ускоряясь.
Здесь мы применили принцип суперпозиции, чтобы рассмотреть движение шара только в одном направлении, игнорируя его движение в направлении к источнику света и движение от него. Мы получили очевидный пример ускоренного движения. Полное движение шара при этом можно представить суперпозицией двух движений под прямым углом друг к другу.
|


|

|

|
Каждый раз, когда шар проходит половину окружности, он изменяет движение на противоположное, совсем так, как если бы он остановился, а потом начал ускоряться в противоположном направлении. Если мы обозначим скорость шара υ, то она должна стать – υ, когда шар появится на противоположной стороне круга. Изменение скорости будет 2 υ, совершенно также, как в случае шара, брошенного вертикально вверх, и возвращающегося на землю со скоростью противоположного направления. Чем быстрее движется шар, тем больше изменение скорости и, следовательно, больше ускорение. Чем быстрее движение, тем сильнее натянута верёвка.
Теперь, когда мы знаем изменение скорости шара, можно найти его среднее ускорение на пути в половину окружности. Чтобы сделать это, мы должны ещё знать, как долго продолжается весь процесс. А это зависит от того, насколько далеко шар уходит от центра своего движения и насколько быстро он движется. Длина окружности радиуса r равна 2π r, и шар проходит половину этого пути. Время необходимое для этого, равно расстоянию, делённому на скорость, 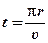 . По определению ускорения мы получаем
. По определению ускорения мы получаем
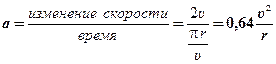 . .
|
Однако мы должны помнить, что это среднее ускорение и общий результат действия силы, которая за время прохождения пол-оборота тянула шар в разных направлениях. В самом деле, в конце пути сила имеет направление прямо противоположное тому, которое было в начале. Поэтому мгновенное ускорение должно быть, конечно же, больше. Однако строгий расчёт мгновенного ускорения требует некоторых математических понятий, которые мы избегаем в этой книге. Поэтому просто представим результат как
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
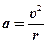 . (3-2) . (3-2)
|
С точки зрения здравого смысла, значение этой формулы понять не трудно. Наличие r в знаменателе просто означает, что требуется большая сила, чтобы удержать объект на малом круге, чем на большом, потому что он вращается на малом быстрее (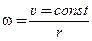 ). Тридцать миль в час – комфортная скорость при смене полосы на шоссе. Но если вы огибаете угол здания в городе на этой скорости, вы услышите громкий визг покрышек. Они визжат потому, что не любят иметь дело с силой, перпендикулярной их движению. В числителе находится υ, и в квадрате, потому что пропорциональность ускорения и скорости нелинейно ухудшает ситуацию: 1) приходится изменять так же бó льшую скорость, 2) это изменение должно происходить более быстро. Радиус безопасного поворота на скорости 60 миль/час не в 2, но в 4 раза больше, чем на скорости 30 миль/час.
). Тридцать миль в час – комфортная скорость при смене полосы на шоссе. Но если вы огибаете угол здания в городе на этой скорости, вы услышите громкий визг покрышек. Они визжат потому, что не любят иметь дело с силой, перпендикулярной их движению. В числителе находится υ, и в квадрате, потому что пропорциональность ускорения и скорости нелинейно ухудшает ситуацию: 1) приходится изменять так же бó льшую скорость, 2) это изменение должно происходить более быстро. Радиус безопасного поворота на скорости 60 миль/час не в 2, но в 4 раза больше, чем на скорости 30 миль/час.
В качестве последнего примера применения этой формулы, рассмотрим путь гоночной машины, проходящей поворот, как показано на рис. 3 - 2.  Хороший гонщик входит в поворот по внешней полосе, движется к внутренней полосе в середине поворота и заканчивает поворот на его внешней границе. Такой путь имеет максимально возможный радиус кривизны, и это позволяет машине поддерживать максимальную скорость.
Хороший гонщик входит в поворот по внешней полосе, движется к внутренней полосе в середине поворота и заканчивает поворот на его внешней границе. Такой путь имеет максимально возможный радиус кривизны, и это позволяет машине поддерживать максимальную скорость.
Если вам не нравится думать о круговом движении с постоянной скоростью как об ускоренном, то это может быть связано с тем неудобством, которое создаёт использование слов то из физики, то из обычной речи, где слово ускорение однозначно предполагает, что что-то начинает двигаться быстрее. В физике же это слово означает любое отклонение от инерциального движения. Мы уже видели, как простое изменение знака решает проблему замедления. В этой части книги мы просто двинулись ещё на один шаг дальше от использования слова ускорение в обычном разговорном языке.
|
|
