
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Математический язык движения
|
|
Скорость – speed (rapidity of movement) и скорость – velocity (quickness, rate of motion) – термины, знакомые каждому, выросшему в XX веке. Два эти термина имеют четкие значения в точном научном языке, и они будут более подробно объяснены далее в Главе 3, но однако даже физики на них поскальзываются и используют их попеременно.
Скорость (speed) можно определить так:
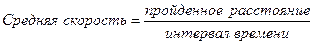 . (1 - 1)
. (1 - 1)
Характеристика «средняя» необходима для понимания того, что скорость может не быть одной и той же в любой части временного интервала. Выраженное более сжато в привычных символах, наше определение станет таким: 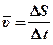 . (1 - 1)
. (1 - 1)
Здесь использована заглавная греческая буква дельта (Δ), чтобы обозначить изменение, или интервал, напоминая нам, что измерение сравнивает два разные положения для двух разных моментов времени. Конечно, мы могли бы использовать и однобуквенные символы для Δ S и Δ t. Но обычный в научном языке прием служит, чтобы подтолкнуть память и передать более полно смысл формулы. Аналогично, черточка над υ является одним из нескольких привычных способов говорить о «средней величине» любого символа под чертой. Использование S как символа расстояния общепринято по некой туманной причине. Частично роль математики в науке состоит в расширении языка, а обозначение выбирается по соображениям ясности.
Если по формуле 1 - 1 рассчитать скорость вашей машины, скажем, за полчаса езды в городе, используя показания одометра и по вашим часам, вы могли бы получить величину 17 миль в час. Но за этой величиной могли бы скрываться 5 минут полной остановки в транспортной пробке и несколько минут смелой езды со скоростью 70 миль в час. Очевидно, множество деталей движения оказываются выпущенными. Чтобы сделать описание более полным, вы могли бы разделить вашу поездку на одноминутные интервалы, подсчитывая среднюю скорость на каждом интервале. Но когда же этот процесс нужно остановить?
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Ответ физика прагматичен: когда я получу достаточное число деталей, чтобы ответить на заданный вопрос. Как грубое приближение к неприятной реальности автовождения в современном городе, ваше первое измерение скорости было достаточно хорошим. Но предположим, вы хотите получить данные, которые позволят вам сказать, насколько хороша ваша машина. Физик мог бы рассуждать так. При резком ускорении или торможении машина может изменять свою скорость на 10 миль/час за одну секунду. То есть если я выберу интервалы по 0, 1 секунды, скорость в начале интервала будет отличаться от скорости в его конце не более чем на 1 милю/час. При интервалах в 1 миллисекунду (1мс = 0, 001с= 1/1000с) я могу определить скорость с точностью 0, 01 миль в час, и так далее.
Рисунок 1 - 1 позволяет графически проиллюстрировать проблему. Если объект движется с постоянной скоростью, то отношению пройденного 
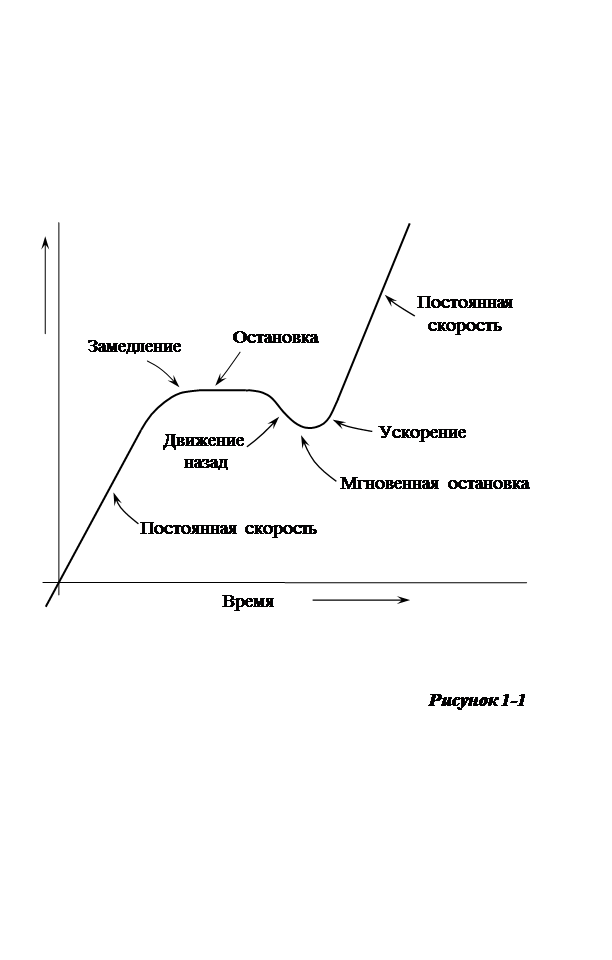
расстояния к прошедшему времени соответствует прямая линия. Чем круче эта линия, тем больше скорость. Крутизна графина называется его наклоном. Когда меняется скорость, изменяется и наклон. Таким образом, график расстояние-время для движения с переменной скоростью будет кривой линией.
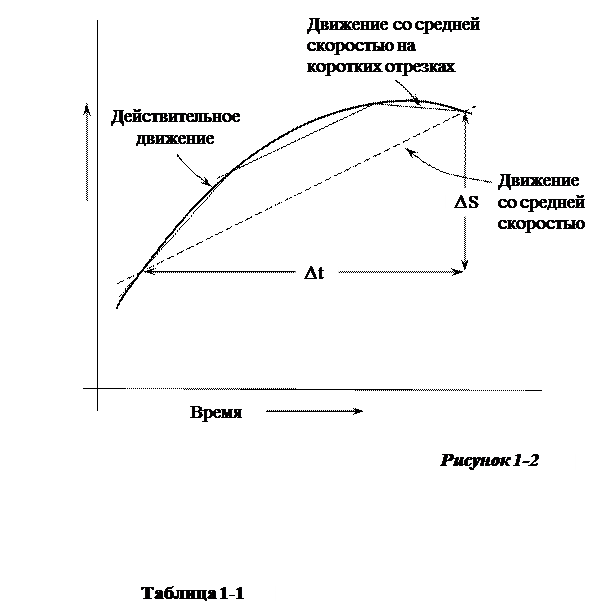
Когда скорость не постоянна, измерение средней скорости упускает многие детали графика. На рисунке 1 - 2 мы видим, что измерения на меньших интервалах более точно представляют действительное движение.
Конечно, для наилучшего описания потребовались бы бесконечно малые интервалы. В этом – смысл приведённых рассуждений, но нам нет нужды быть столь буквальными. Существо вопроса в том, что независимо от желаемой точности описания, её можно получить, просто выбирая интервал достаточно малым. Это убеждает нас в том, что можно говорить о скорости в конкретный момент. Спидометр автомобиля прямо измеряет эту скорость. При этом можем отбросить качественное прилагательное «средняя».
Нашим следующим шагом будет поиск способа, чтобы указать, как быстро меняется сама скорость. Ведь и автомобильные фирмы заявляют, что их изделие будет делать «от 0 до 60 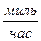 за 6 секунд». Мы можем выразить нечто похожее таким же способом, каким мы определили скорость, назвав новую величину средним ускорением
за 6 секунд». Мы можем выразить нечто похожее таким же способом, каким мы определили скорость, назвав новую величину средним ускорением 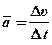 .
.
По этому определению ускорение, заявленное в рекламе автомобиля, составит 10 миль в час за секунду. Физик содрогнется от использования часов в качестве единицы времени для скорости и секунд для ускорения и предпочтёт метры в сек за секунду для единицы ускорения, которая сократится до мс -2. Как и при измерении скорости, Δ υ вычисляется путём вычитания скорости в начале временного интервала из скорости в конце его.
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
Концепция ускорения трудна для понимания, так как является ступенчатой абстракцией, выделенной из прямого наблюдения некоторого объекта в конкретном месте в данный момент времени («здесь и сейчас»). Используя экономическую аналогию, можно сказать, что цена яиц в супермаркете – это конкретный факт. Утверждение, что скорость инфляции составляет 10 % в год, является абстракцией, такой же, какая использовалась при измерении скорости. Печальная новость, что ситуация ухудшается, т.к. скорость инфляции два месяца назад составляла только 8 % в год, является следующей ступенью абстракции, точно соответствующей понятию ускорения. Если мы разделим изменение скорости инфляции, которое равно 10–8=2 процента, на время между измерениями этой скорости (это 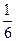 года), мы получим «ускорение» цен 12% на год в квадрате, и аналогия будет полной.
года), мы получим «ускорение» цен 12% на год в квадрате, и аналогия будет полной.
Понятие ускорения одинаково хорошо подходит для процессов увеличения и уменьшения скорости. В последнем случае изменение скорости
| Время, с | Скорость, м/с | Путь падения, м |
| Средняя скорость = 30 м/с |
(и, следовательно, ускорение) будет отрицательным. Таким образом, нам не нужна отдельная концепция замедления.
Важно твёрдо различать понятия скорости и ускорения, т.к. они могут быть полностью независимыми друг от друга и даже иметь разные знаки. Когда машина движется вперёд с возрастающей скоростью, и скорость и ускорение положительны. Если же машина движется вперёд с уменьшением скорости, то скорость положительна, но ускорение отрицательно. Для машины, которая едет назад с возрастанием скорости, и ускорение и скорость отрицательны. Но если машина замедляется, двигаясь назад, её скорость отрицательна, но ускорение положительно, т.к. скорость становится менее отрицательной, т.е. изменяется в положительном направлении!
Если это последнее предложение вам понятно, у вас очень хорошая голова для физики.
Возвращаясь к рисунку 1-1, становится ясно, что когда имеется ускорение, линия, описывающая движение, должна быть кривой. Если скорость объекта возрастает, график искривляется вверх, если скорость уменьшается, график искривляется вниз.
|
|
