
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метод сечений.
|
|
Кинематический анализ фермы
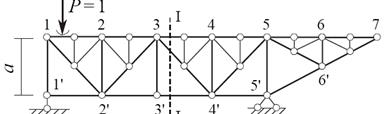
Ферма состоит из 23 стержней (С = 23), соединенных между собой в 13 узлах (У = 13), опирается на землю с помощью трех опорных стержней (С оп = 3). Определяем число степеней свободы системы по формуле W = 2 У – С – С оп = 2 13 – 23 – 3 = 0. Так как W = 0, ферма статически определима и может быть геометрически неизменяемой.
Метод вырезания узлов.
Разрезая мысленно стержни, сходящиеся в данном узле, и уравновешивая внешнюю силу, приложенную к нему, продольными усилиями, действующими по направлению каждого стержня, получаем необходимые уравнения для определения этих сил. При составлении уравнений равновесия предполагаем все внутренние силы растягивающими и действующими по направлению от узла.
метод сечений.
Разрезав мысленно ферму на две части и отбросив одну из них, можно составить три уравнения равновесия для оставшейся части фермы. Если в разрез попадают только три стержня, то при помощи этих уравнений можно определить усилия в разрезанных стержнях.
15. Линии влияния усилий в стержнях междуопорной и консольной части фермы. Способы их проверки.
Следует различать два вида сечений: междуопорное и консольное. Междуопорное сечение разделяет ферму на двечасти, в каждой из которых находится одна из опор. Консольное сечение так же делит ферму на две части, причем одна из них свободна от опорных реакций. Способ построения линии влияния зависит от вида сечения.
Междуопорное сечение:
1) строят линии влияния опорных реакций;
2) проводят сечение не более чем через три стержня, в том числе и ра ссматриваемый;
3) составляют уравнения Y = 0 или М = 0 правой части фермы, когда груз
Р = 1 слева от сечения, и левой части, когда груз справа от сечения. При этом в уравнение должны входить только искомая продольная сила и одна из опо рных реакций;
4) передаточная (соединительная) прямая находится между узлами рассеченного стержня грузового пояса, левая прямая – слева от передаточной, правая – справа;
5) если используется уравнение моментов, то левая и правая прямые пересекаются под моментной точкой.
Консольное сечение:
1) проводят сечение не более чем через три стержня, в том числе и ра ссматриваемый;
2) составляют уравнения Y = 0 или М = 0, когда груз Р = 1 слева и справа от сечения, всегда рассматривая равновесие отсеченной консоли. При этом в уравнение должны входить только искомая продольная сила и груз Р = 1;
3) если используется уравнение моментов, то координату z груза отсчитывают от моментной точки;
4) передаточная (соединительная) прямая находится между узлами рассеченного стержня грузового пояса, левая прямая – слева от передаточной, правая – справа.
16. Шпренгельные фермы. Линии влияния в их стержнях
Шпренгель – это дополнительная двухопорная фермочка, вводимая в с остав каждой панели для восприятия местной нагрузки и передающая давление на узлы основной фермы.
Преобразуем нашу ферму в шпренгельную, установив одноярусные шпре нгели в верхнем грузовом поясе (рисунок 6). Для примера рассмотрим только ее междуопорную часть.
Определяются эти усилия из тех же уравнений, что и ранее, только меняются границы передаточных прямых.
+ 15 билет (способы построения).
17. Трехшарнирные системы, их параметры, классификация. Определение опорных реакций в трехшарнирной арке от неподвижной вертикальной нагрузки
Трёхшарнирнойназывается геометрически неизменяемая система, состоящая из трёх дисков, попарно соединённых тремя шарнирами.
Трёхшарнирной аркойназывается трёхшарнирная система, два основных диска которой являются криволинейными стержнями, обращёнными, как правило, выпуклостью навстречу действующей нагрузке.
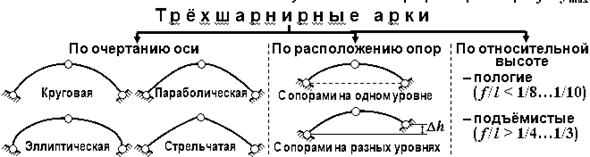
Трёхшарнирной рамойназывается трёхшарнирная система, два основных диска которой являются ломаными или прямолинейными стержнями.
В опорах арки А и В возникают наклонные опорные реакции, которые можно разложить на четыре составляющие: вертикальные V A и V B, горизонтальные H A и H B (рисунок 3, а).
Вертикальные составляющие V A и V B равны опорным реакциям соответствующей балки б 189 кН
V A = V б A =, 159 кН
V B = V б B =.
Горизонтальные составляющие Н A и Н B равны между собой. Обозначим их
Н (распор) и определим по формулам:
Hа= Hб= H, Н= M бC/ f,
где М Сб – изгибающий момент в сечении С соответствующей балки.
Для рассматриваемой арки М Сб = 1392 кН × м, Н = 1392/8 = 174 кН.
18. Определение внутренних усилий в трехшарнирной арке от неподвижной вертикальной нагрузки. Построение эпюр
Внутренние усилия в k -ом сечении арки рассчитываем по формулам:
а) изгибающий момент
M k = M бk - H × y k;
б) поперечная сила
Q k = Q k б cosj k - H sin j k;
в) продольная сила ()
N k = - Q k бsin j k + H cosj k.
Расчет ведем в табличной форме (таблица 2). Величины z k, y k, sin jk, cos jk
берем соответственно из граф 2, 3, 6, 7 таблицы 1, значения M kб, Q kб – из эпюр M б, Q б.
По полученным ординатам М, Q, N строим эпюры
19. Особенности передачи нагрузки на арку. Линии влияния опорных реакций в трехшарнирной арке
Линии влияния строим в предположении, что по арке движется сосредот оченная сила (груз) Р = 1, направленная вертикально вниз. Ее положение задается координатой z, отсчитываемой от левой опоры.
Вертикальные реакции V A и V B в арке равны реакциям V Aб и V Bб в соответствующей балке (рисунок 5, б), поэтому их линии влияния строим аналогичнолиниям влияния V Aб и V Bб (рисунок 5, в, г).
å M B = 0; - V A l + P (l - z) = 0, V A = (l - z) l;
0 A å M =; V B l - Pz = 0, V B = z l.
На опоре А V A z =0 = 1, V B z =0 = 0; на опоре В V A z = l = 0, V B z = l =1.
Линию влияния распора Н построим статическим методом. Рассмотрим два
положения подвижного груза (таблица 3).

Слева от шарнира С изображаем левую прямую, справа – правую. Их пересечение дает линию влияния Н (рисунок 5, д).
20. Линии влияния изгибающих моментов в трехшарнирной арке
Для построения линии влияния изгибающего момента в заданном сечении арки (сечение 3) М 3 (рисунок 6, а) применяем способ наложения. При этом используем зависимость М = М б – Н * у.
То есть, чтобы получить л. в. М 3, необходимо построить линии влияния М 3б и(– Н * у 3), а затем сложить их соответствующие ординаты.
Для расчета ординат л. в. М 3б рассмотрим два положения груза Р = 1 на соответствующей балке (таблица 4).
По полученным ординатам в одном масштабе по одну сторону от базы строим линии влияния М 3б и (– Н * у 3) (рисунок 6, б, в). Далее совмещаем их наодной базе и суммируем соответствующие ординаты (рис унок 6, г).Характерные ординаты линии влияния М 3 вычисляем из подобия треугольников. По полученным ординатам изображаем л. в. М 3 на горизонтальной базе(рисунок 6, д).
21. Линии влияния поперечных сил в трехшарнирной арке
Для построения линии влияния поперечной силы Q 3 в сечении 3 арки (рисунок 7, а) используем зависмость:
Q = Q б cosj - H sin j. Следовательно, чтобы получить л. в. Q 3, необходимо построить линии влияния Q 3б * cos j3 и (– Н * sin j3) и сложить их соответствующие ординаты. Для расчета ординат л. в. Q 3б рассмотрим два положения груза Р = 1 на соответствующей балке (таблица 6).
По полученным ординатам в одном масштабе по одну сторону от базы строим линии влияния Q 3б cos j3 и (– Н * sin j3) (рисунок 7, б, в). Совмещаем ихна одной базе и суммируем соответствующие ординаты (рисунок 7, г).Характерные ординаты линии влияния Q 3 определяем из подобия треугольников. Изображаем л. в. Q 3 на горизонтальной базе (рисунок 7, д).
22. Линии влияния продольных сил в трехшарнирной арке
Для построения линии влияния продольной силы N 3 в сечении 3 арки (рисунок 8, а) используем формулу
N = -(Q б sin j + H cosj). Следовательно, чтобы получить л. в. N 3, необходимо построить линии влияния Q 3б * sin j3 и Н * cos j3, сложить их соответствующие ординаты и умножить на (–1).
Расчет ординат л. в. Q 3б * sin j3 и л. в. Н * cos j3 ведем в табличной форме (таблицы 8 и 9), используя данные таблиц 3 и 6.
По полученным ординатам в одном масштабе по разные стороны от базы строим линии влияния Q 3б sin j3 и Н cos j3 (рисунок 8, б, в). Совмещаем ихна одной базе, суммируем соответствующие ординаты и умножаем на (–1) (ри-сунок 8, г).Характерные ординаты линии влияния N 3 вычислим из подобия треугольников. Изображаем л. в. N 3 на горизонтальной базе.
23. Рациональное очертание оси трехшарнирной арки. Определение напряжений в арке. Расчетное положение нагрузки на арке
Арка рационального очертания - такая арка, в каждом сечении которой при вертикальной нагрузке определенного вида изгибающий момент равен нулю. Чтобы 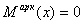 в соответствии с (5.9) необходимо добиться выполнения равенства
в соответствии с (5.9) необходимо добиться выполнения равенства 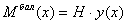 , т.е. задать очертание арки по формуле
, т.е. задать очертание арки по формуле 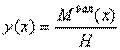 . Поскольку
. Поскольку 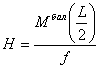 получим
получим 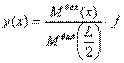 (5.17).
(5.17).
Поскольку 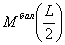 и f не зависят от координаты x, из (5.17) следует, что y(x) должна быть пропорционально изгибающему моменту в балке, соответствующей рассматриваемой арке. В соответствии принципом суперпозиций с увеличением нагрузки в k раз все силовые факторы, а значит соотношение
и f не зависят от координаты x, из (5.17) следует, что y(x) должна быть пропорционально изгибающему моменту в балке, соответствующей рассматриваемой арке. В соответствии принципом суперпозиций с увеличением нагрузки в k раз все силовые факторы, а значит соотношение 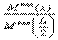 не изменится при пропорциональном изменении нагрузки. Таким образом, если очертание арки y(x) выполнено в соответствии с формулой (5.17) для какой-то нагрузки, то и при пропорциональном ее увеличении или уменьшении моментов в арке не возникнет. Другое дело, если изменится вид нагрузки, например, равномерно распределенная нагрузка будет заменена сосредоточенными силами.
не изменится при пропорциональном изменении нагрузки. Таким образом, если очертание арки y(x) выполнено в соответствии с формулой (5.17) для какой-то нагрузки, то и при пропорциональном ее увеличении или уменьшении моментов в арке не возникнет. Другое дело, если изменится вид нагрузки, например, равномерно распределенная нагрузка будет заменена сосредоточенными силами.
Итак, для построения арки рационального очертания для нагрузки определенного вида достаточно построить эпюру изгибающего момента в балке, соответствующей данной арке, и, задавшись значением f, определить очертание арки по формуле (5.17). В частности, рациональным очертанием для арки, загруженной равномерно распределенной нагрузкой, будет параболическое очертание, поскольку изгибающий момент в соответствующей балке меняется по закону параболы.
Определение напряжений в арке
Определяем наибольшие и наименьшие нормальные напряжения:
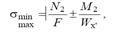 Геометрические характеристики сечения арки: площадь F = bh. момент сопротивления
Геометрические характеристики сечения арки: площадь F = bh. момент сопротивления 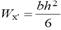 . Проверяем выполнение условия прочности max (|smin|, smax) £ R.
. Проверяем выполнение условия прочности max (|smin|, smax) £ R.
Расчетное положение нагрузки на арке
Невыгоднейшее положение внешней нагрузки на соор ужении определим приближенным методом, т. е. рассмотрим раздельно линии влияния N 3 и М 3.
Определяем расчетное положение нагрузки по положительной части л. в. М 3. Для этого располагаем распределенную нагрузку над участком л. в. М 3, имеющим знак ≪ +≫, а сосредоточенную силу – над максимальной ординатой этого участка. Находим +М 3max, умножая интенсивность распределенной нагрузки q на площадь линии влияния М 3, находящуюсяпод этой нагрузкой, а величину сосредоточенной силы P – на ординату л. в. под силой.
Определяем расчетное положение нагрузки по отрицательной части л. в. М 3. Для этого располагаем распределенную нагрузку над участком л. в. М 3, имеющим знак ≪ –≫, а сосредоточенную силу – над максимальной ординатой этого участка. Находим –М 3max и соответствующее ему значение продольной силы N 3.
Определяем расчетное положение нагрузки по л. в. N 3. Для этого располагаем распределенную нагрузку над всей л. в. N 3, так как вся она имеет знак ≪ +≫, а сосредоточенную силу – над максимальной ординатой л. в. Находим N 3max и соответствующее ему значение момента М 3 при данном положении нагрузки. 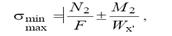
24. Цель определения перемещений в упругих системах. Принцип возможных перемещений в упругих системах. Действительная и возможная работа
Принцип возможных перемещений
В общем случае этот принцип формулируется так: для равновесия системы необходимо и достаточно, чтобы сумма возможных работ всех действующих на нее активных сил на любых бесконечно малых возможных перемещениях точек системы была равна нулю: swe + sw i = о,
где sWe - возможная работа внешних сил на возможных перемещениях; SW' — возможная работа внутренних сил на возможных деформациях. s – дельта.
Принцип Лагранжа в упругих системах
Для равновесия упругой системы необходимо и достаточно, чтобы сумма возможных работ всех действующих на систему сил на любых малых возможных перемещениях ее точек была равна нулю: We + Wi = о,
где We - возможная работа внешних сил; Wi - возможная работа внутренних сил (напряжений).
Упругие перемещения точек в линейно деформируемых системах хотя и конечны, но весьма малы по сравнению с размерами элементов. Эти перемещения можно принять в качестве возможных, так как они удовлетворяют наложенным связям.
Действительной называется работа данных сил (внешних или внутренних) на перемещениях и деформациях, вызванных этими же силами.
Возможной называется работа внешних или внутренних сил на возможных перемещениях или деформациях.
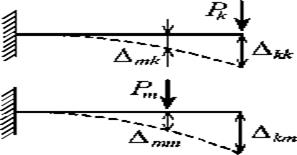
Действительная работа силы Pk при статическом действии ее на упругую систему равна половине произведения конечного значения этой силы на окончательное значение соответствующего ей перемещения ∆ kk (теорема Клапей
рона; справедлива для любой линейно деформируемой системы):
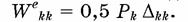
При вычислении возможной работы силы Рk следует брать не половину, а полную величину произведения каждой
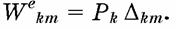 силы на соответствующее возможное перемещение
силы на соответствующее возможное перемещение
 С помощью принципа перемещений может быть доказано свойство двойственности статических и геометрических уравнений.
С помощью принципа перемещений может быть доказано свойство двойственности статических и геометрических уравнений.
25. Формула Максвелла-Мора
Одним из основных методов определения перемещений является метод Максвелла – Мора (если конструкция может рассматриваться как линейно деформируемая стержневая система) по формуле
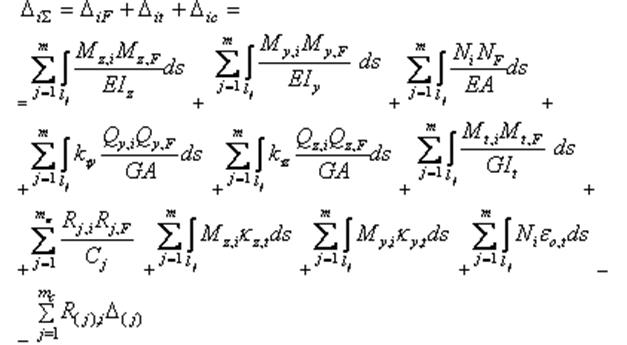

Для плоских стержневых систем формула Максвелла – Мора упрощается и в случае только силового воздействия принимает следующий вид:
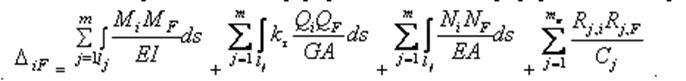
26. Правило Верещагина
Для вычисления интеграла Мора можно использовать способ Верещагина:
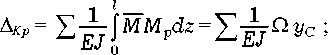
где EJ - изгибная жесткость; Ω - площадь «грузовой» эпюры Мр;
Ус~ ордината «единичной» эпюры М, взятая под центром тяжести эпюры Мр.
Следует помнить, что ордината ус должна быть обязательно взята из прямолинейной эпюры. Результат будет положительным, если центр тяжести одной эпюры и ордината ус расположены по одну сторону от оси стержня.
Если обе перемножаемые эпюры линейные, то операция перемножения обладает свойством коммутативности. В этом случае безразлично, умножается ли площадь первой эпюры на ординату второй или площадь второй эпюры на ординату первой.
27. Применение формулы Симпсона для перемножения эпюр (две трапеции, парабола и трапеция)
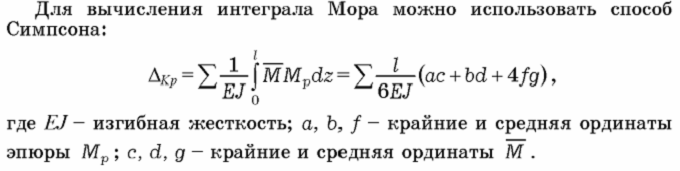

28. Статически неопределимые системы (ст. н. с.). Особенности работы, методы расчета. Типы связей ст. н. с. Степень статической неопределимости.




В строительной механике различают следующие два классических метода расчета статически неопределимых систем; метод сил и метод перемещений. При расчете по методу сил основными искомыми величинами являются усилия в лишних связях. Знание усилий в лишних связях позволит по методу сечений, как это было показано в первом разделе учебника, выполнять полный расчет по определению усилий, возникающих в поперечных сечениях элементов заданной системы. При расчете по методу перемещений основными искомыми величинами являются перемещения узловых точек, вызванные деформацией системы. Знание этих перемещений необходимо и достаточно для определения всех внутренних усилий, возникающих в поперечных сечениях элементов, заданной системы.
29. Основная система, канонические уравнения метода сил, их смысл. Коэффициенты уравнений, их смысл и способы вычисления.
Известно, что основная система определяется из заданной путем отбрасывания лишних связей и приложением соответствующих усилий, возникающих в отброшенных связях в заданной системе. При этом основная система должна быть статически определимой и геометрически неизменяемой.
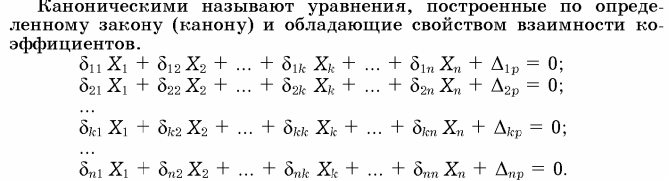
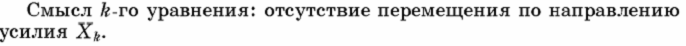

Для определения перемещений, являющихся коэффициентами канонических уравнений, используем формулу Мора. При этом влиянием продольных и поперечных сил пренебрегаем и считаем, что перемещения обусловлены только действием изгибающих моментов. Используем следующие формулы:
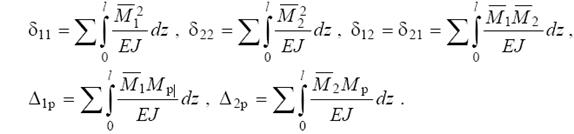
30. Порядок расчета рам методом сил. Способы построения эпюр М, Q, N.
В методе сил в качестве основной выбирается обычно статически определимая система, получаемая из заданной п раз статически неопределимой системы путем отбрасывания п жестких связей или постановкой (введением) шарниров. Этими жесткими связями могут быть жесткие опоры или связи, соединяющие одну часть стержня с другой. Усилия взамен отброшенных связей прикладываются в месте разреза или введенного шарнира в виде поперечных, продольных сил или изгибающих моментов.
Можно выбрать различные варианты основной системы. Необходимо, чтобы полученные таким образом основные системы были статически определимыми и кинематически неизменяемыми.
Канонические уравнения метода сил составляются для основной системы из условия равенства нулю перемещений по направлению внешних лишних связей и относительных перемещений по направлению внутренних лишних связей.
Вычислим ординаты окончательной эпюры изгибающих моментов М. Для этого необходимо сложить грузовую эпюру Мр и единичные M1, M2, умноженные на соответствующие значения X1, X2 (рисунок 13): M = Mp +M1X1 +M2X2 Подсчитаем значения изгибающего момента в характерных точках 1, …, 7
заданной системы (рисунок 14, а). По полученным ординатам строим эпюру
Эпюра поперечных сил Q строится по готовой эпюре изгибающих моментов М, где эпюра М ограничена параболой, т. е. действует равно-
мерно распределенная нагрузка, поперечную силу определяем с помощью ба-лочной аналогии, представим этот стержень отдельно, как балку на двух опорах. Приложим к его концам возникающие в системе внутренние моменты,
взятые из эпюры М, Определим опорные реакции Y1, Y2 полученной балки, далее вычисляем поперечные силы в точках и полученные значения откладываем на эпюре Q и соединяем прямой линией.
Также можно строить обычным способом сечений. И там где эпюра М прямолинейна, используем дифференциальную зависимость Q = dM/dz. По рассчитанным ординатам строим эпюрупоперечных сил.
Эпюру продольных сил N строим по готовой эпюре Q. Вначале определим значение N в точке 3. Мысленно проведем в ней сечение, отбросим левую часть и рассмотрим равновесие правой (рисунок 19, а). Очевидно, что N(3) = 0. Аналогично находим N(4) = 0. Рассмотрим равновесие жесткого узла рамы 2–3–5. Приложим к нему поперечные и продольные силы в каждой из точек (рисунок 19, б). При этом поперечные силы направим так, чтобы они поворачивали узел по часовой стрел-
ке (т. е. считаем их положительными), а численное значение и знак возьмем из эпюры Q. Составим уравнения равновесия узла. Сумма проекций всех сил на вертикальную ось. Сумма проекций на горизонтальную ось. По полученным данным строим эпюру N.
31. Проверки, используемые в процессе расчета рамы методом сил.
Выполним проверку правильности вычисления X1, X2, подставив их значе-
ния в систему
|
|