
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Опис за картами. Опис - традиційний і загальновідомий прийом аналізу карт
|
|
Опис - традиційний і загальновідомий прийом аналізу карт. Його мета - виявити досліджувані явища, особливості їхнього розміщення і взаємозв'язку. Науковий опис, який складається за картами, повинне бути логічним, впорядкованим і послідовним. Він відрізняється відбором і систематизацією фактів, введенням елементів порівняння і аналогій. В опис часто вводять кількісні показники та оцінки, включають таблиці і графіки. В кінці формулюються висновки і рекомендації.
Описи можуть бути загальними комплексними (такі, наприклад, загальногеографічні описи) або поелементними (скажімо, опис тільки карстового рельєфу).
В даний час, коли для аналізу карт широко залучаються математичні методи і комп'ютерні технології, опис не втратив свого значення. Виконуючи якісний аналіз явищ і їхніх взаємозв'язків, досвідчений дослідник здатний часом прийти до висновків більше глибоких, ніж якби він додержувався формальних алгоритмів і розкладав дослідження на елементарні логіко-математичні операції. Описи, засновані, основним чином, на візуальному аналізі карт, корисні тим, що дозволяють скласти образне і цілісне подання про досліджуваний об'єкт і зробити висновки синтетичного характеру, застосовуючи для цього неформальні евристичні підходи.
12.5. Графічні прийоми
Графічні прийоми включають побудову за картами різних профілів, розрізів, графіків, діаграм, блок-діаграм та інших дво- і тривимірних графічних моделей.
Для аналізу серій карт різної тематики зручно використовувати комплексні профілі, на яких поєднуються, наприклад, гіпсометричний профіль, геологічний розріз, ґрунтово-рослинний покрив, графіки гідрокліматичних показників і т.п.
Аналогічно можна побудувати і комплексні соціально-економічні розрізи, поєднавши за обраним напрямком графіки густоти населення, гістограми його вікового складу, зайнятості, криві енергозабезпеченості території, розораності земель і т.п. Такі побудови потрібні для наочного подання зв'язків між явищами і районуванням території за комплексом показників.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
В географічних дослідженнях часто використають рози-діаграми, які наочно передають переважне орієнтування лінійних об'єктів, наприклад геологічних розламів, річкових долин, транспортних шляхів та ін. Довжинакожного променя рози-діаграми i- гоазимута пропорційна сумарній довжині лінійних елементів того ж азимута.
На рис. 12.4 показані дві рози-діаграми. Одна відображає розподіл спрямованих орогідрографічних елементів: вододілів, гряд, уступів, прямих відрізків рік, наскрізних долин ярів та ін., а на інший цей розподіл поєднано з розою-діаграмою тектонічних тріщин даного району. Перша роза-діаграма побудована за топографічною картою, а друга - за геологічною. Їхня схожість наглядно свідчить про тектонічну зумовленість річкових долин у цьому районі.
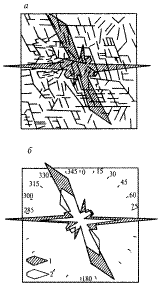
Рис. 12.4.Рози-діаграми, побудовані по топографічній і геологічній картах.
Зв'язки між явищами, показаними на картах різної тематики, можна наочно відобразити і проаналізувати на блок-діаграмах.
Для побудови блок-діаграм застосовують різні види проектування (рис. 12.5). Аксонометричні блок-діаграми проектують за допомогою системи паралельних променів, ніби центр проектування є в нескінченності. При цьому деформуються кутові співвідношення, але горизонтальний масштаб блок-діаграми за осями х, y, z залишається постійним, що зручно для вимірів. Інший тип - перспективні блок-діаграми. У цьому випадку промені, що проектують, виходять із однієї або двох точок, що дає більш виразне зображення. Змінюючи положення центрів проектування, можна «повертати» блок-діаграми або «нахиляти» їх, забезпечивши найбільш вигідний огляд і підкреслюючи потрібні деталі. Однак при хорошій наочності блок-діаграми з однієї і двома точками проектування незручні для вимірів, оскільки масштаб змінюється по всіх осях відповідно до законів перспективи. Іноді блок-діаграми отримують у вигляді серії вертикальних перерізів або роблять у них вирізи, для того щоб показати внутрішню будову блоку.
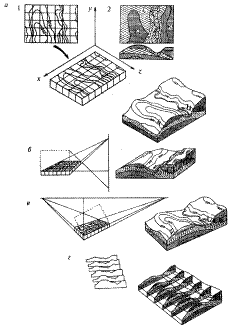
Рис. 12.5.Блок-діаграми.
а - аксонометрична (1 і 2 - фрагменти вихідних топографічної і геологічної карт); б - перспективна з однією точкою проектування; в - перспективна з двома точками проектування; г - система паралельних розрізів.
Масштаби за різними осями блок-діаграм можуть бути неоднаковими, наприклад для наочного зображення рельєфу вертикальний масштаб збільшують у два-три рази відносно горизонтального. Рельєф стає більше опуклим, всі нерівності добре помітні, однак при цьому виникають поля невидимості (рис. 12.6). Розтягання за висотою призводить до появи полів невидимості.
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
Якщо за однією з осей задати шкалу часу, то можна побудувати метахронну блок-діаграму. Вона відобразить зміну стану явища в часі, наприклад хід середніх місячних температур на поверхні. На рис. 12.7 показана метахронна блок-діаграма, що характеризує розподіл швидкостей вітру за висотою в різні сезони року над Тихим океаном вздовж меридіана 180°. Для її побудови зняті дані з карт п'яти висотних рівнів (0, 4, 8, 12 і 16 км над рівнем моря) для чотирьох місяців (лютий, травень, серпень, листопад). Таким чином, ця метахронна блок-діаграма синтезує інформацію, отриману з 20 карт.
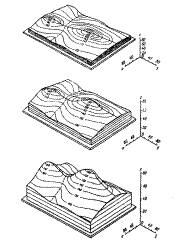
Рис. 12.6. Блок-діаграма з різними масштабами по вертикалі.

Рис. 12.7. Метахронна блок-діаграма. Показано розподіл швидкостей вітру над Тихим океаном на висотах до 16 км (вісь H) вздовж 180° в різні сезони року (T).
Для побудови блок-діаграм застосовують графопобудовувачі або виводять тривимірні зображення на екран комп'ютера. Спеціальні анімаційні програми дозволяють варіювати масштаби в будь-якому напрямку, підбирати найбільш вигідний ракурс огляду і навіть обертати блок-діаграми на екрані, розглядаючи їх з різних сторін.
До графічних прийомів відноситься також дії з поверхнями, показаними на різних картах: графічне додавання, обчислення однієї поверхні з іншої, множення на число та ін. Цим користуються при балансових розрахунках, наприклад для оцінки обсягу знесеного ерозією матеріалу, визначення сумарної кількості опадів за кілька місяців і т.п.
12.6. Графоаналітичні прийоми
Графоаналітичні прийоми аналізу карт - картометрія і морфометрія - призначені для виміру і обчислення за картами показників розміру, форми і структури об'єктів. Ці прийоми найбільш докладно розроблені в картографічному методі дослідження.
Методи картометрії дозволяють безпосередньо вимірювати наступні показники:
· географічні і прямокутні координати;
· довжини прямих і звивистих ліній, відстані;
· площі;
· об’єм;
· вертикальні і горизонтальні кути та кутові величини.
Крім того, в рамках картометрії досліджується точність вимірів за картами.
На відміну від картометрії, морфометрія займається розрахунком показників форми і структури об'єктів. Найбільш вживані наступні групи показників і коефіцієнтів:
· форма об'єктів;
· кривина ліній і поверхонь;
· горизонтальне розчленовування поверхонь;
· вертикальне розчленовування поверхонь;
· ухили і градієнти поверхонь;
· щільність, концентрація об'єктів;
· густота, рівномірність мереж;
· складність, роздробленість, однорідність/неоднорідність контурів.
Морфометричні показники обчислюються на основі картометричних даних і як правило відносні. Наприклад, горизонтальне розчленовування - це відношення сумарної довжини ерозійних форм до одиниці площі, звивистість лінії - відношення довжини кривої до довжини плавної, що огинає, щільність - кількість об'єктів на одиницю площі, роздробленість - відношення середнього розміру контуру до площі цілого району і т.д. Найчастіше береться відношення саме до площі, тому питання про розміри ділянок, у межах яких ведуться обчислення тих або інших показників, дуже істотне. Від цього залежать точність обчислень і репрезентативність морфометричних показників.
Можливі три варіанти розрахунку:
· за регулярною геометрично правильною сіткою квадратів, шестикутників, кружків і т.п. - цей спосіб зручний тим, що площі комірок рівновеликі;
· за природними ареалами (природними районами, ландшафтами, водозбірними басейнами);
· за еталонними ділянками.
В результаті на основі обчислених показників створюються морфометричні карти. Багато з них широко відомі і входять до складу атласів, наприклад морфометричні карти рельєфу, густини населення, густоти дорожньої мережі та ін. Ці карти виконуються у вигляді ізолінійних (точніше, псевдоізолінійних) полів або у формі картограм за розрахунковими комірками або ареалами.
Точні картометричні і морфометричні визначення досить трудомісткі і неможливі без використання спеціальних інструментів (циркулів-вимірників, планіметрів та ін.), вони вимагають скрупульозного контролю похибок, які виникають і залежать від точності самих карт, інструментів, похибок вимірів, деформації паперу, на якій надрукована карта, і багато чого іншого. Все це довгий час заважало широко застосовувати графоаналітичні прийоми у повсякденній практиці. Ситуація змінилася з розвитком комп'ютерних технологій і впровадженням статистичних підходів.
Яскравим прикладом є вимір довжин звивистих ліній (рік, границь, берегових ліній та ін.), що завжди вважалося дуже трудомісткою процедурою. У класичній картометрії для цього завжди використали циркуль-вимірник за допомогою якого проміряють звивисту лінію на карті. Легко зрозуміти, що замість довжини звивистої лінії в цьому випадку виходить довжина ламаної, що складається з хорд, які стягають відрізки кривої. Тому отримана довжина завжди буде коротшою довжини звивистої лінії, яка вимірювалася.
У картометрії існують десятки емпіричних способів введення виправлень і різного роду редукцій для корекції результату. Всі вони досить громіздкі і у підсумку дають відносну похибку порядку 3-5%. Справа ще більше ускладнюється, якщо вимірюється не одна, а сукупність звивистих ліній у межах деякої ділянки, наприклад сумарна довжина русел рік у деякому водозбірному басейні.
Інший підхід пропонує імовірна картометрія. Її методи дозволяють значно спростити масові виміри за картами при деякому зниженні точності. Зокрема, пропонується використати метод відомого французького натураліста XVIII ст. Ж. Бюффона. На ділянку, яка вимірюється накладається палетка паралельних ліній або квадратів і підраховується кількість перетинівліній палетки зі звивистими лініями. Тоді сумарна довжина звивистих ліній обчислюється на основі досить простої імовірнісної залежності.
Схожі імовірнісні способи, що виключають трудомісткі безпосередні виміри за картами, розроблені і для визначення площ та об’ємів, а це істотно спрощує обчислення багатьох морфометричних показників розчленування, густоти, щільності об'єктів і т.п. На рис. 12.8 зображена ділянка карти з ізолініями і блок-діаграма тієї ж ділянки. Середні висоти обчислюють за картами в центрі квадратів за допомогою інтерполяції між ізолініями.

Рис. 12.8. До визначення об’ємів. Ділянка ізолінійної карти, розділеної на квадрати, і блок-діаграма тієї ж ділянки.
Імовірнісні підходи і комп'ютерні технології повністю змінили вигляд сучасної картометрії і морфометрії, зробивши їх доступними широкому колу фахівців.
Одна з характерних рис морфометрії - множинність показників. Існують, наприклад, десятки способів характеристики форм (планових обрисів) об'єктів, показаних на картах. Найчастіше намагаються апроксимувати контури ареалів на карті якими-небудь геометричними фігурами: неправильними багатокутниками, еліпсами, колами і т.п., а потім знаходять їхні числові параметри. Наприклад, обчислюють різні співвідношення між сумами сторін багатокутників або беруть відношення радіусів кіл - вписаного в контур і описаного навколо нього. Найбільш вживаним, хоча далеко не єдиним, показником форми є коефіцієнт, пропорційний відношенню квадрата периметра об'єкта до його площі. Значення показника є вищим, чим більше відхилення розглянутої фігури від форми кола. Цим користуються для оцінки форм ландшафтних, ґрунтових, зоогеографічних та інших ареалів, кратерів і інших тектонічних структур, островів і т.п.
При оцінці кривини звивистих ліній також використається безліч показників. Звивистість русла несхожа на зрізаність морського узбережжя або на замкнутий контур озера, непорівнюнна звивистість горизонталей і границь ґрунтових ареалів і т.д. В морфометрії застосовують різні показники (рис. 12.9): відносна звивистість, звивистість загальних обрисів, загальна звивистість, частота звивин.

Рис. 12.9. До визначення показників звивистості незамкнутих (а) і замкнутих (б) ліній (l - звивиста лінія; s – плавна, що обгинає; d - замикаюча лінія).
Сучасна математика пропонує для оцінки звивистості ліній використовувати поняття про фрактали. В основі фрактальної геометрії лежить поняття про ієрархічну схожість об'єктів на самих себе. Інакше кажучи, звивисті лінії можна поділити на ділянки, кожний з яких схожий на всю лінію (рис. 12.10). Для визначення фрактальної розмірності лінійного об'єкта необхідно виміряти його довжину з певним кроком.

Рис. 12.10. Об'єкти схожі на самих себе і мають фрактальну розмірність.
Часто вживаним морфометричним показником є щільність об'єктів, тобто їх кількістьна одиницю площі карти.
При аналізі за картою рельєфу та інших поверхонь широко застосовують показники горизонтального, вертикального розчленування і ухилу (градієнта) поверхні.
Горизонтальне розчленування характеризується сумарною довжиною ліній, що розчленовують, наприклад тальвегів, що припадають на одиницю площі.
Вертикальне розчленування визначають як різницю максимальної і мінімальної висот в межах якої-небудь ділянки, наприклад в річковому басейні.
Спочатку картометрія і морфометрія розвивалися стосовно до аналізу рельєфу за топографічними картами (морфометрія рельєфу - один з основних розділів геоморфології), але потім їх стали широко використати в геології, планетології, ландшафтознавстві, океанології, економічній географії і географії населення, екології. Так сформувався особливий напрямок - тематична морфометрія. В загальному вигляді розділи і об'єкти дослідження тематичної морфометрії представлені в табл. 12.1.
Таблиця 12.1
Розділи і об'єкти тематичної морфометрії
| Розділи тематичної морфометрії | Основні об'єкти дослідження |
| Геоморфологічна морфометрія | Форми рельєфу суші і морського дна, палеорельєф, морфоструктури, неотектонічні структури |
| Структурна морфометрія | Геолого-структурні поверхні, розлами, лінеаменти, кільцеві структури |
| Геофізична морфометрія | Геофізичні поля, їхні компоненти, нормальні і аномальні складові |
| Морфометрія планет і небесних тіл | Планетарні структури, рельєф планет, лінеаменти, кратери |
| Гідрологічна морфометрія (суші) | Структура гідромережі, форма, розмір гідрографічних об'єктів, рельєф русла рік |
| Морфометрія морів і океанів | Форма, розмір акваторій, структура водних мас, розподіл фізико-хімічних параметрів вод, біологічних ресурсів, розміри забруднень |
| Ландшафтометрія | Структура ландшафтної оболонки, конфігурація і розподіл ландшафтів |
| Педометрія (морфометрія ґрунтів) | Структура ґрунтового покриву, форма і розподіл ґрунтових ареалів, ґрунтово-геохімічні аномалії, ерозія ґрунтів |
| Морфометрія рослинного покриву | Структура рослинного покриву, форма і розміри ареалів рослинності, обсяг біомаси |
| Еколого-географічна морфометрія | Джерела несприятливих впливів на середовище, природні та антропогенні фактори забруднення, структура ареалів забруднення, шляхи міграції та потоки забруднення |
| Медико-географічна морфометрія | Структура і форма ареалів захворювань, вогнища епідемій, шляхи їхнього переміщення |
| Соціально-економічна морфометрія | Структура розселення, розміщення об'єктів промисловості і сільського господарства, конфігурація транспортних мереж, мереж обслуговування та ін. |
Розмаїття об'єктів, зображених на тематичних картах, веде до певної диференціації прийомів і показників. Так, у геоморфології, геології, геофізиці доводиться мати справу головним чином з поверхнями і тілами, які зображаються на ізолінійних картах. Ландшафтна, ґрунтова, геоботанічна морфометрія найчастіше оперує з ареалами і якісним фоном, а соціально-економічна морфометрія - переважно з пунктами і мережами.
12.7. Прийоми математико-картографічного моделювання
Формалізоване картографічне зображення добре пристосовано для математичного аналізу. Як згадувалося вище, кожній точці карти з координатами х і у поставлено у відповідність лише одне значення картографуючого параметра z, що дозволяє представити зображення даного явища як функцію z = F(х, у). В інших випадках картографічне зображення зручно представити як поле випадкових величин і скористатися для його аналізу ймовірносно-статистичними методами.
В принципі майже всі розділи математики можна застосовувати для обробки і аналізу картографічного зображення. Проблема лише в тому, щоб підібрати математичну модель і, головне, дати надійне змістовне пояснення результатам моделювання. Досить надійно в картографічний аналіз ввійшли деякі розділи чисельного аналізу, багатомірної статистики, теорії ймовірностей і теорії інформації.
Апроксимації. Під апроксимаціями в математиці розуміють заміну (наближення) складних або невідомих функцій іншими, більш простими функціями, властивості яких відомі.
Існують різні способи апроксимації. Це звичайні алгебраїчні багаточлени, ортогональні багаточлени Чебишева і Лежандра, які певним чином спрощують обчислення, сплайн-функції та ін. Відзначимо, що у всіх випадках задача зводиться до того, щоб апроксимуюче рівняння найкраще описувало вихідну поверхню з мінімальним відхиленням.
На рис. 12.11 показане послідовне покращення апроксимацій на прикладі нескладних поверхонь. Апроксимація 1-го порядку (лінійне рівняння) дає площину, що відображає тільки загальний ухил поверхні, це дуже грубе, занадто загальне наближення. Поверхня 2-го порядку вже більше схожа на вихідну модель, а апроксимація 3-го порядку (кубічне рівняння) дає досить добре наближення до вихідної поверхні.
Тригонометричні функції дозволяють описувати складні, дуже розчленовані поверхні, а сферичні функції застосовують, якщо при обчисленнях не можна знехтувати кривиною земної поверхні. Апроксимація за допомогою подвійних рядів Фур'є, представлена на рис 12.12, ілюструє поступове ускладнення поверхні за рахунок додавання двомірних синусоїд з різними фазами і амплітудами. Комп'ютерне моделювання дозволяє виконувати подібні апроксимації для поверхонь будь-якої складності, обчислюючи рівняння високого порядку, що містять часом кілька десятків членів розкладу.

Рис. 12.11. Апроксимації поверхонь:
а - блок-діаграма вихідної поверхні; б, в, г - блок-діаграми апроксимуючих поверхонь відповідно 1, 2 і 3-го порядків.
У дослідницькій практиці апроксимації використовують для аналітичного опису поверхонь (полів), які зображені на картах, і виконання з ними різних дій: додавання, віднімання, інтегрування і диференціювання, для підрахунку об’ємів тіл, обмежених цими поверхнями, і розв’язку безлічі інших задач. Один з напрямків використання апроксимацій - розклад поверхонь на складові, що дозволяє виділяти і аналізувати нормальні та аномальні фактори розвитку і просторового розташування явищ.
Прийоми математичної статистики. Ця група прийомів математико-картографічного моделювання призначена для вивчення за картами просторових і часових статистичних сукупностей і утворених ними статистичних поверхонь.

Рис. 12.12. Схема тригонометричної апроксимації поверхні за допомогою послідовного накладення двомірних синусоїдальних хвиль (по Дж. Дэвісу).
Статистичний аналіз картографічного зображення переслідує головним чином три мети:
· вивчення характеристик і функцій розподілу явища;
· вивчення форми і зв'язків між явищами;
· оцінка ступеня впливу окремих факторів на досліджуване явище і виділення провідних факторів.
В основі будь-якого статистичного дослідження є вибірка, тобто деяка множина однорідних величинзнятих з карти за регулярною сіткою точок (систематична вибірка), у випадково розташованих точках (випадкова вибірка), на опорних ділянках або за районами (районована вибірка).
Вибіркові дані групують за інтервалами, складають гістограми розподілу (рис. 12.13) і потім обчислюють різні статистики - кількісні показники, що характеризують просторовий розподіл досліджуваного явища. Найбільш вживані показники - середнє арифметичне, середнє вагове арифметичне, середнє квадратичне, дисперсія, варіація та ін. Крім того, за допомогою спеціальних показників (критеріїв згоди) можна оцінити відповідність даного конкретного розподілу тому або іншому теоретичному закону розподілу. Наприклад, встановити, чи узгоджується емпіричний розподіл висот рельєфу з кривою нормального розподілу, як це показано на рис. 12.13, чи підпорядковується іншій функції.

Рис. 12.13. Фрагмент карти рельєфу (а) з сіткою точок регулярної вибірки (виходи сітки відзначені на рамці), гістограма і крива розподілу висот (б): ω — частота; h — висоти рельєфу.
Інша типова дослідницька задача - оцінка взаємозв'язку між явищами - вирішується за допомогою добре розробленого в математичній статистиці апарата теорії кореляції.
В практичних дослідженнях взаємозв'язків часто необхідно отримати попередню наближену оцінку коефіцієнта кореляції. В простих випадках це можна зробити, використовуючи представлення про статистичні поверхні.
Прийоми теорії інформації. Ці прийоми використовують для оцінки ступеня однорідності і взаємної відповідності явищ, досліджуваних за картами.
Мова йде про основну функцію теорії інформації - ентропії. В термодинаміці ентропія характеризує ступінь безладу у фізичній системі, у теорії зв'язку - ступінь невизначеності переданих повідомлень, а в картографічному аналізі ця функція виявилася досить зручною для оцінки ступеня однорідності/ неоднорідності картографічного зображення.
Інформаційні функції використовуються для оцінки ступеня взаємної відповідності (збігу) контурів на різних картах. У цьому випадку вони виконують роль своєрідних показників взаємозв'язку явищ на зразок коефіцієнтів кореляції.
Тема 13. КАРТОГРАФІЯ І ГЕОІНФОРМАТИКА
13.1. Географічні інформаційні системи
13.2. Підсистеми ГІС
13.3. Геоінформатика – наука, технології, виробництво
13.4. Геоінформаційне картографування
|
|
