💸 Как сделать бизнес проще, а карман толще?

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое раписание, но и напоминать клиентам о визитах тоже. Проблема в том, что средняя цена по рынку за такой сервис — 800 руб/мес или почти 15 000 руб за год. И это минимальный функционал. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!

Ошибки измерения угла вследствие неточности центрирования визирных марок и теодолита.

Рассмотрим ошибки редукции и центрирования более подробно.

Пусть теодолит установлен в точке В – вершине измеряемого угла безошибочно, а визирная марка в точке А установлена не точно, т.е. ось вращения визирной марки проходит через точку А´

На рисунке

е₁ - линейный элемент редукции;

Θ - угловой элемент редукции.

Визирная марка относительно истинного положения – точки А - может занимать любое другое положение. От этого будет меняться величина ошибки α или элементы редукции. Рассмотрим вариант, когда линейный элемент неизменен, а меняется лишь угловой элемент редукции. Тогда точка А´ движется по окружности, т.е. число перемещений

n = 2·π /d Θ (17.6)

Выразим α из треугольника АВ А´.

(е₁ / sin α) = (S/ sin Θ) (17.7)

Длина визирного луча S много больше линейного элемента редукции, а величина ошибки α мала в сравнении с величиной измеряемого угла. По этой причине можно считать, что стороны треугольника ВА и В А´ равны. Следовательно,

α = (е₁/ S) · ρ · sin Θ (17.8)

Таких значений α будет бесконечно много. Средняя квадратическая ошибка редукции для одного направления может быть найдена по формуле Гаусса.

m_редА ² = [α ² ] /n (17.9)

С учетом выражения (17.8) будем иметь:

m_редА ² = [((е₁/ S) · ρ · sin Θ)² ] /n (17.10)

Приняв во внимание (17.6), получим:

m_редА ² = (е₁² /2·π S²) · ρ ² · Σ sin² Θ d Θ (17.11)

Заменим знак суммы интегралом с пределами от 0 до 2·π.

m_редА ² = (е₁² /2·π S²) · ρ ² · ∫ sin² Θ d Θ (17.12)

Выполнив интегрирование, получим

m_редА = (е₁/√ (2·π) S) · ρ (17.13)

Для измеренного угла β в случае неточной установки двух визирных марок ошибка составит:

m_ред ² = m_редА ² + m_редС ² (17.14)

m_ред ² = (е₁² /2 S₁²) · ρ ² + (е₁² /2 S₂²) · ρ ² = (е₁² · ρ ²) /2·(1/ S₁² + 1/ S₂²) (17.15)

Ошибка редукции не зависит от величины измеряемого угла. Чем больше разница в длинах визирных лучей (сторон измеряемого угла), тем больше ошибка редукции. Чем короче сторона хода, тем больше ошибка редукции при приблизительно равных сторонах. Необходимо соблюдать требования Инструкции к минимальной длине стороны.

Значение линейного элемента редукции позволяет выбрать средство центрирования визирных марок. Это значение будет зависеть от значения ошибки редукции.

Ошибка центрирования будет рассмотрена с помощью следующего рисунка.

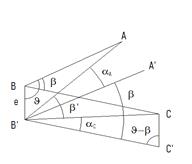Пусть визирные цели установлены в точках А и С безошибочно, а ось вращения прибора проходит через точку В´. Тогда фактически будет измеряться угол А В´ С. Его значение будет отличаться от истинного (угла АВС) на величину α - ошибки измерения угла. Построим из точки В´ линии, параллельные истинному положению визирных лучей.

Отрезок В В´ - линейный элемент центрирования – обозначим е, а угол АВ В´ - угловой элемент центрирования – обозначим Θ.

Рассуждая по аналогии с предыдущим выводом, можно записать выражение (17.16) для возможного количества установок прибора относительного верного положения – точки В.

n = 2·π /d Θ (17.16)

Из рисунка и по построению следует, что

β + α _А = β ´ + α _С (17.17)

β ´ = β + α _А - α _С (17.18)

Исходя из структуры результата измерения, α _А - α _С есть ошибка в измерении горизонтального угла, вызванная неточным центрированием теодолита, т.е. ошибкой центрирования. Получим выражение для этой ошибки, рассмотрев два треугольника:

Δ А В´ А´ (α _А) и Δ СВ´ С´ (α _С).

е / sin α _А = S₁ / sin Θ (17.19)

α _А = (е/ S₁) · ρ · sin Θ (17.20)

е / sinα _С = S₂/ sin(Θ - β) (17.21)

α _С = (е/ S₂) · ρ · sin (Θ - β) (17.22)

α _А - α _С = (е/ S₁) · ρ · sin Θ - (е/ S₂) · ρ · sin (Θ - β) (17.23)

При бесконечно большом числе установок теодолита таких разностей будет n.

Тогда средняя квадратическая ошибка центрирования может быть вычислена по формуле Гаусса.

m_центр ² = [(α _А - α _С) ² ] /n (17.24)

С учетом(17.16) получим

m_центр ² = [((е/ S₁) · ρ · sin Θ - (е/ S₂) · ρ · sin (Θ - β)) ² ] d Θ /2·π (17.25)

Вынесем из-под знака суммы общие множители и получим

m_центр ² = (е² · ρ ²)/ 2·π · [(1/ S₁) ² · sin² Θ + (1/ S₂) ² · sin² (Θ - β) –

- (2/ S₁S₂) · sin² Θ · sin² (Θ - β)] d Θ (17.26)

Заменим знак суммы интегралом и проинтегрируем полученное выражение. Приняв следующие условия. Пределы интегрирования от 0 до 2·π, длины визирных лучей одинаковы и равны S_. В итоге получим

m_центр ² = (е² / S²) · ρ ² · (1- cos β)] (17.27)

Ошибка центрирования будет зависеть от величины измеряемого угла β. Чем ближе будет значение угла к 180 ̊, тем ошибка будет больше. Поэтому при вытянутом ходе следует особо тщательно центрировать теодолит на пунктах хода. Кроме этого. На величину этой ошибки оказывают влияние длины визирных лучей. Чем короче сторона хода, тем ошибка центрирования больше. Из формулы (17.27) можно выразить линейный элемент центрирования и определиться с методикой установки прибора на пункте.

Для уменьшения влияния ошибок центрирования и редукции при производстве измерений в полигонометрических ходах используют трехштативную систему.

Суть ее заключается в том, что на трех смежных пунктах штативы центрируются один раз, а затем последовательно переставляются в подставках прибор и визирные марки.