Примеры. Углом между прямой и плоскостью будем называть угол, образованный прямой и её проекцией наплоскость

УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮ

Углом между прямой и плоскостью будем называть угол, образованный прямой и её проекцией наплоскость. Пусть прямаяи плоскость заданы уравнениями

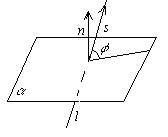Рассмотрим векторы и . Если угол между ними острый, то он будет 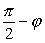, где φ – угол между прямой и плоскостью. Тогда .

Если угол между векторами и тупой, то он равен . Следовательно . Поэтому в любом случае . Вспомнив формулу вычисления косинуса угла между векторами, получим .

Условие перпендикулярности прямой и плоскости. Прямая и плоскость перпендикулярны тогда и только тогда, когда направляющий вектор прямой и нормальный вектор плоскости коллинеарны, т.е. .

Условие параллельности прямой и плоскости. Прямая и плоскость параллельны тогда и только тогда, когда векторы и перпендикулярны.

Примеры.

1. Написать уравнение плоскости, проходящей через точку М ₁(2; -3; 4) параллельно прямым и .

Так как M₁ Î α, то уравнение плоскости будем искать в виде

.

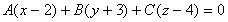Применяя условие параллельности прямой и плоскости, получим систему линейных уравнений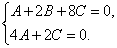

Отсюда

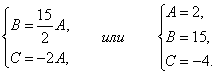
Итак, или .

1. Найти угол между прямой и плоскостью .

Направляющий вектор прямой . Нормальный вектор плоскости . Следовательно,

1. Найдите точку, симметричную данной М (0; -3; -2) относительно прямой .

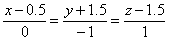Составим уравнение плоскости α перпендикулярной l. M Î α, 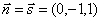. Следовательно, или .

Найдём точку пересечения прямой l и α:

Итак, N (0.5; -0.5; 0.5). Пусть искомая точка М ₁ имеет координаты М ₁(x, y, z). Тогда очевидно равенство векторов 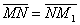, т.е. (0, 5; 2, 5; 2, 5)=(х -0.5; у +0.5; z -0.5). Откуда x =1, y =2, z =3 или М ₁(1; 2; 3)..

№41

ЦИЛИНДРИЧЕСКИЕ ПОВЕРХНОСТИ

Определение. Цилиндрической поверхностью называется поверхность, описываемая прямой (называемой образующей), остающейся параллельной некоторой данной прямой и пересекающей данную линию Z (называемую направляющей).

Рис.1

Пусть направляющая определяется уравнениями

и , (1)

а m, n, p – координаты направляющего вектора образующей цилиндрической поверхности. Канонические уравнения образующей имеют вид

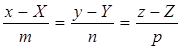, (2)

где x, y, z – текущие координаты, X, Y, Z – координаты точки, принадлежащей направляющей.

Исключая X, Y, Z из четырёх уравнений (1) и (2), получим искомое уравнение цилиндрической поверхности.

Рассмотрим частный случай. Пусть уравнение поверхности не содержит одной из переменных, для определённости z, то есть .

На плоскости Oxy это уравнение определяет некоторую кривую линию L.

В пространстве этому уравнению удовлетворяют все те точки пространства, первые две координаты которых совпадают с координатами линии L, то есть те точки пространства, которые проектируются на плоскость Oxy в точки линии L. Совокупность всех точек есть прямая параллельная оси Oz, проходящая через точку . Следовательно, совокупность всех точек, удовлетворяющих уравнению , есть поверхность, описываемая прямой, параллельной оси Oz и пересекающих линию L, то есть цилиндрическая поверхность.

Рис.2

Аналогично, – уравнение цилиндрической поверхности, образующая которой параллельно оси Oy; 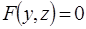- уравнение цилиндрической поверхности с образующей, параллельной оси Ox.

Перечислим прямые цилиндры с образующей, параллельной оси Oz:

1) 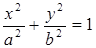– эллиптический цилиндр с направляющей – эллипсом в плоскости Oxy. Частным случаем эллиптического цилиндра является прямой круговой цилиндр, то есть .

Рис 3.

2) - гиперболический цилиндр с направляющей – гиперболой плоскости Oxy.

Рис.4

3) 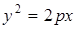- параболический цилиндр с направляющей – параболой в плоскости Oxy.

Рис.5

КОНИЧЕСКИЕ ПОВЕРХНОСТИ

Определение. Конической поверхностью называется поверхность, описываемая прямой (образующей конуса), проходящей через данную точку (вершину конуса) и пересекающей данную линию (направляющую конуса).

Рис.6

Пусть направляющая задана уравнениями

и (1)

вершиной является точка M_o(x_o, y_o, z_o).

Канонические уравнения образующей конуса, проходящей через точку М_о и точку М(X, Y, Z), лежащую на направляющей, имеют вид:

. (2)

Исключая из (1) и (2) X, Y, Z, получим искомое уравнение конической поверхности.

Пример 1. Составить уравнение конуса с вершиной в начале координат и направляющей , .

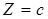Образующая имеет канонические уравнения

, то есть .

Исключая X, Y, Z из уравнений

,

,

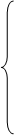
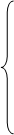
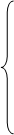
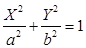
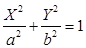
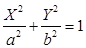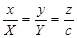
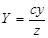
получим уравнение эллиптического конуса: 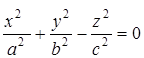. (3)

Рис.7

Пример 2. Составить уравнение конуса с центром в начале координат и направляющей , .

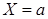Образующей искомого конуса является прямая:

.

Исключая X, Y, Z из уравнений направляющей и образующей, получим уравнение или .

Обратим внимание, что полученное уравнение совпадает с уравнением (3).

Этот же конус можно получить, взяв в качестве направляющей параболу. Объясняется это сечениями конуса различными плоскостями. Подробнее об этом ниже.

ПОВЕРХНОСТИ ВРАЩЕНИЯ

Составить общее представление о большинстве поверхностей второго порядка можно, рассматривая поверхности вращения.

Определение. Поверхностью вращения вокруг оси d называется поверхность, каждое сечение которой, перпендикулярное оси d, является окружностью с центром, лежащим на этой оси.

Рассмотрим линию L, которая вместе с осью d лежит в плоскости Р. Будем вращать эту линию вокруг оси, при этом каждая точка линии опишет окружность, а вся линия L опишет поверхность вращения.

Введём систему координат. Выберем начало прямоугольной декартовой системы координат на оси d, ось Oz направим вдоль оси d, ось Ox поместим в плоскости P перпендикулярно оси Oz. Допустим, что линия L имеет в этой системе координат уравнение . Выведем уравнение поверхности вращения этой линии вокруг оси Oz. Для этого выберем на поверхности произвольную точку M(x, y, z). Расстояние от неё до оси Oz равно . Через точку М проходит окружность, описываемая при вращении некоторой точки плоскости Р. Обозначим эту точку М_о, а её координаты в системе Oxz (x_o, y_o) (в системе Oxyz она будет иметь координаты (x_o, 0, z_o)), очевидно что , .

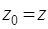Точка М лежит на поверхности вращения тогда и только тогда, когда на ней лежит точка М_о, а, следовательно, и симметричная с ней относительно оси Oz точка . Чтобы точки М_о и лежали на поверхности, необходимо и достаточно, чтобы координаты хотя бы одной из них удовлетворяли уравнению линии L, то есть чтобы . Получим условие для координат точки

М . (1)

Это и есть уравнение поверхности вращения линии L вокруг оси Oz.

Случай, когда уравнение (1) не имеет вещественных решений, не исключается. В этом случае говорят о мнимой поверхности.

Эллипсоиды*

Эллипсоидом называется поверхность, задаваемая в некоторой декартовой системе координат уравнением

(3.26)

Числа а, b, с называются полуосями эллипсоида.

Выясним форму эллипсоида. Поскольку текущие переменные х, у, z входят в уравнение (3.26) в четных степенях, эллипсоид симметричен относительно каждой координатной плоскости. Рассмотрим сечение эллипсоида координатными плоскостями. Плоскость 0 ху имеет уравнение , поэтому сечение эллипсоида плоскостью 0 ху задается системой уравнений:

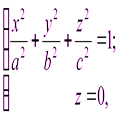
откуда имеем

(3.27)

Система (3.27) показывает, что плоскость 0 ху пересекает эллипсоид по эллипсу с полуосями а, b. Аналогично для плоскостей 0 yz, 0 xz соответственно получаем в сечении эллипсы:

Можно показать, что любая плоскость, параллельная координатной плоскости, пересекает эллипсоид по некоторому эллипсу. Общий вид эллипсоида представлен на рис. 3.36.

Гиперболоиды*

Однополостным гиперболоидом называется поверхность, задаваемая в некоторой декартовой системе координат уравнением

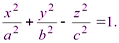(3.28)

Эта поверхность имеет три плоскости симметрии (координатные плоскости). Выясним, какую форму имеет однополостный гиперболоид, для этого рассмотрим сечения его координатными плоскостями. В плоскости 0 yz получаем:

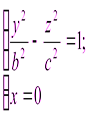
(3.29)

– гиперболу с действительной полуосью b и мнимой полуосью с (в плоскости 0 уz) (рис. 3.37). Аналогично,

(3.30)

В сечении гиперболоида плоскостью 0 xz также получаем гиперболу с действительной полуосью а и мнимой полуосью с. Пересекая гиперболу плоскостью 0 ху в сечении получаем эллипс:

с полуосями а и b. Всякая плоскость, параллельная плоскости 0 ху (она имеет уравнение z = h, h R), пересекает однополостный гиперболоид по линии:

(3.31)

Преобразуем систему (3.31):

(3.32)

Система (3.32) задает эллипс (рис. 3.37), лежащий в плоскости z = h и имеющий своими полуосями: .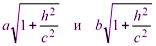

Однополостный гиперболоид (3.28) не пересекает ось 0 z, она служит осью симметрии для гиперболы (3.29) и гиперболы (3.30) и называется осью гиперболоида (3.28).

Уравнение также задает однополостный гиперболоид, но его осью служит 0 у, а для однополостного гиперболоида осью является ось 0 х.

Д 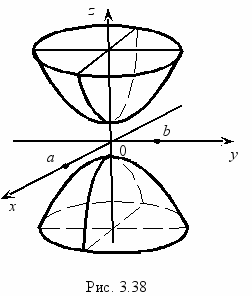вуполостным гиперболоидом называется поверхность, определяемая в некоторой декартовой системе координат уравнением:

Рассмотрим сечения этой поверхности координатными плоскостями:

(3.33)

(3.34)

Система (3.33) задает в плоскости 0 xz гиперболу с действительной полуосью с и мнимой полуосью а, система (3.34) – в плоскости 0 уz также гиперболу с действительной полуосью с и мнимой – b. С плоскостью 0 ху двуполостный гиперболоид пересечения не имеет. Действительно, системе: 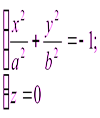не удовлетворяет ни одна точка пространства.

Рассмотрим сечение этого гиперболоида плоскостью, параллельной 0 ху и удаленной от нее на расстояние : . Из этой системы получаем систему: , которая задает эллипс (рис. 3.38) в плоскости z = h с полуосями .

Ось 0 z является общей осью симметрии для гипербол (3.33) и (3.34) и называется осью двуполостного гиперболоида. Уравнения:

(3.35)

(3.36)

также задают двуполостные гиперболоиды, для (3.35) осью служит 0 у, а для (3.36) – 0 x.

Параболоиды*

Эллиптическим параболоидом называется поверхность, определяемая в некоторой декартовой системе координат уравнением:

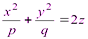, (3.37)

где р и q одного знака.

П
усть 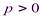, , тогда z 0, причем z = 0 при х = 0 и у = 0. Следовательно, с плоскостью 0 ху эта поверхность имеет единственную общую точку 0(0, 0, 0). Рассмотрим сечение параболоида плоскостью z = h, (эта плоскость параллельна плоскости 0 ху):

Видим, что сечение – эллипс с полуосями . Сечения с плоскостями 0 ху и 0 уz являются параболами:

причем 0 z являетсяих общей осью (рис. 3.39). Oсь 0 z является осью параболоида (3.37). Если , , 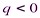то параболоид будет располагаться ниже плоскости 0 ху.

Гиперболическим параболоидом называется поверхность, уравнение которой имеет вид:

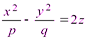, (3.38)

где р и q одинакового знака.

П
усть , . Рассмотрим сечения этой поверхности плоскостями 0 xz и 0 yz, получим, соответственно, параболы , причем ветви первой направлены вверх, а ветви второй – вниз (рис. 3.40). С плоскостью 0 ху параболоид имеет сечение , что равносильно двум системам:

(3.39)

Системы (3.39) задают в плоскости 0 ху две прямые, проходящие через начало координат.

Пусть плоскость параллельна 0 ху и удалена от неена h (), тогда в пересечении с параболоидом (3.38) получится гипербола

(3.40)

При гипербола (3.40) имеет действительную полуось , мнимую полуось (рис. 3.40, L ₃). При 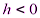гипербола (3.40) имеет действительную полуось 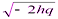, а мнимую – (рис. 3.40, L ₄).
^

№42