Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Алгебраический метод построения области устойчивости

Построение области устойчивости в аналитическом виде по коэффициенту усиления электронного усилителя осуществляется с помощью модифицированного критерия Гурвица (критерия Льенара-Шипара [25]) для характеристического уравнения

,

некоторые коэффициенты которого зависят от .

Условие устойчивости системы с учетом выражения матрицы Гурвица

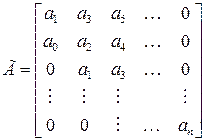
записывается в виде неравенств:

1) , ;

2) 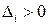, 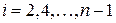для нечетных (индексы 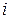четные);

или

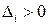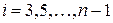, для четных (индексы 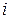нечетные);

где – главный диагональный минор матрицы Гурвица.

При условие устойчивости определяется неравенствами 1) и неравенством .

При 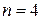условие устойчивости с учетом предыдущего выражения определяется неравенствами 1) и неравенством .

При 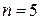условие устойчивости с учетом предыдущих выражений , 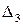определяется неравенствами 1) и неравенствами

,

.

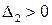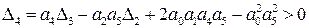Построение области устойчивости по коэффициенту усиления рассмотрим на примере передаточной функции разомкнутой системы схемы А:

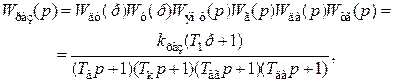
где ; для одного из вариантов задания найдены параметры 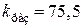, с, с, с, с, с.

Поскольку здесь коэффициент пропорционален , то найдем сначала область устойчивости по коэффициенту . Для вычисления необходимых главных диагональных миноров матрицы Гурвица воспользуемся M-функцией:

function gurviz

syms p kpas % символьные переменные

% Исходные данные

T1=0.4; Tv=0.04; Tk=0.2; Tvg=0.96; Tdv=0.38; % постоянные времени

Wpas=kpas*(T1*p+1)/((Tv*p+1)*(Tk*p+1)*(Tvg*p+1)*(Tdv*p+1));

n=4; % порядок системы

% Определение коэффициентов характеристического уравнения

Wz=simplify(1/(1+Wpas)); [num, den]=numden(Wz);

N=n+1; M=N-2; ac=coeffs(den, p); Dp=vpa(collect(den/ac(N)), 6)

% Формирование определителей матрицы Гурвица G, которые

% должны быть больше нуля

for i=1: N; b1(i)=ac(N+1-i); end; b=b1/ac(N);

N=n+1; M=N-2; KN=N-fix(N/2)*2;

for K=1: M; IK=fix((K+1)/2); KK=(-1)^K;

K1=IK+fix((KK+KN)/2)+fix(N/2)-1;

for I=IK: K1; I1=(I-IK+1)*2-fix((KK+1)/2); G(K, I)=b(I1); end; end

nk=fix((n-1)/2); for id=1: nk; nid=n-1-2*(nk-id);

for i=1: nid for j=1: nid; Gd(i, j)=G(i, j); end; end

detG=vpa(det(Gd), 6), cdet=sym2poly(detG); kras1=roots(cdet); kras1'

end

Здесь для выполнения M-функции вводятся исходные данные: постоянные времени передаточной функцию разомкнутой системы, ее вид и порядок . В результате выполнения программы на печать выводится выражение полинома характеристического уравнения замкнутой системы

p^4+33.6732*p^3+237.939*p^2+(137.061*kpas+541.393)*p+342.654+342.654*kpas

выражения необходимых для проверки определителей

561220.*kpas+.365609e7-18785.8*kpas^2

и значения kpas, при которых определители обращаются в ноль:

35.3761 -5.5014

Таким образом, для данного примера условиями устойчивости замкнутой системы являются неравенства

,

,

,

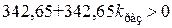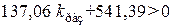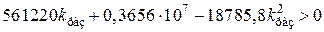из которых следует искомая область устойчивости .