Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сопротивления прямой, обратной и нулевой последовательностей трансформатора.

Метод симметричных составляющих

Рисунок 3.1 – Метод симметричных составляющих

Согласно методу несимметричную систему токов можно разложить на три симметричные: прямой, обратной и нулевой последовательности, то есть

,

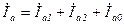(3.1.1)

,

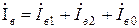(3.1.2)

.

(3.1.3)

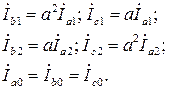
(3.14)

где 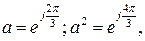(3.15)

причем 1 + а + а ² = 0.

Если взять за основу составляющие фазы а, то можно записать:

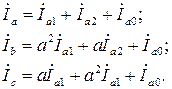
(3.16)

Решив уравнения (3.16) относительно I_{а 1}, I_{а 2} и I_{а 0}, получим::

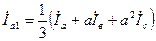,	(3.1.7)
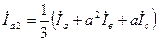,	(3.1.8)
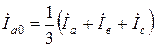;	(3.1.9)

Приведённые выражения могут быть справедливы и для системы напряжений.

Каждой системе токов соответствует своя система сопротивлений: прямой, обратной и нулевой последовательности. Зная сопротивления отдельных последовательностей, находят для них распределения напряжений, а затем, пользуясь методом наложения, определяют истинные токи и напряжения.

Сопротивления прямой, обратной и нулевой последовательностей трансформатора.

Можно легко показать, что при допущении I ₀ = 0 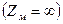имеет место соотношение

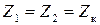
(3.1.9)

Поэтому эти системы можно анализировать совокупно, то есть

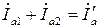,	(3.1.10)
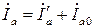,	(3.1.11)

и т.п.

Для суммарной системы токов и напряжений прямой и обратной последовательности справедливы выражения:

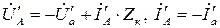
(3.1.12)

в соответствии с упрощенной схемой замещения.

Рисунок 3.1.3 –Схема замещения трансформатора для токов прямой и обратной последовательности

Для нулевой последовательности схема замещения и её параметры имеют ряд особенностей, связанных с тем, что токи нулевой последовательности совпадают по фазе и могут существовать только при наличии нулевого провода (также, как и токи н. с. 3-й гармоники)

а) токов нулевой последовательности нет (Y/Y), 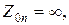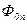также нет, поскольку U _1Л – симметричны; ∆ /Y – тоже

б) токи нулевой последовательности протекают с двух сторон (в фазах): Y₀/Y₀ – такого не бывает; бывает ∆ /Y₀ – для нулевой последовательности трансформаторов ведёт себя также, как и для прямой Z_моп < Z_м.

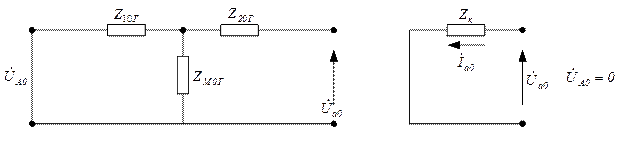Рисунок 3.1.4 – Схема замещения для токов нулевой последовательности для схемы ∆ /Y₀

Здесь фазные напряжения нулевой последовательности на стороне ∆ равны нулю, то есть это система фазных напряжений симметрична

в) токи нулевой последовательности протекают с одной стороны Y/Y₀

Это единственный случай, когда недопустимо пренебречь током намагничивания нулевой последовательности, так как для этой системы трансформатор работает в режиме холостого хода. Его схема замещения

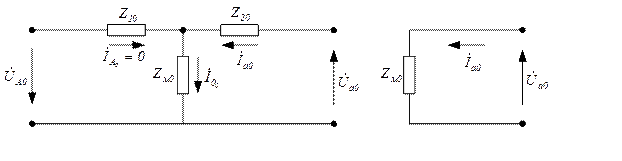Рисунок 3.1.5 – Схема замещения для токов нулевой последовательности для схемы Y/Y₀

В этом случае Z₀ определяется Z_м0, и в основном конструкцией сердечника.

В броневых и пятистержневых трансформаторов поток нулевой последовательности замыкается по магнитопроводу, поэтому он достигает величины основного потока и

Z₀ = Z_м.

В трёхстержневых трансформаторах поток нулевой последовательности замыкается по воздуху и через крепёжные детали, поэтому Z₀ здесь значительно меньше.

.4 Переходные процессы в трансформаторах

При изменении режима работы трансформатора в нормальных условиях (включение трансформатора в сеть, резкое изменение нагрузки) или в аварийных (внезапное к. з.) в трансформаторах возникают переходные процессы, во время которых токи могут во много раз превышать номинальные установившиеся значения. Это влияет:

1) на тепловой режим;

2) на возникновение электромагнитных тел.

Поэтому переходные процессы надо уметь анализировать и учитывать при проектировании трансформаторов. Будем рассматривать переходные режимы последовательно: от простого к сложному.

Включение трансформатора под напряжением на холостом ходу

Пусть трансформатор включается на напряжение

,

(3.4.1)

где – ψ -фаза включения, определяющая значение 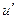в момент включения. Тогда переходный процесс описывается выше приведённым уравнением. Это – обыкновенное неоднородное дифференциальное уравнение1-го порядка.

Из курса математики известно, что решение состоит из двух слагаемых:

1) вынужденной, где ψ -начальная фаза включения

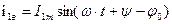
(3.4.2)

–установившийся ток, протекающий под действием источника, где

,

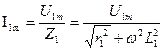(3.4.3)

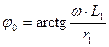;	(3.4.4)
х 1 = ω L 1

2) свободная апериодическая, не поддерживается внешними источником и затухает до нуля с постоянной времени

.

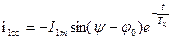(3.4.5)

1-я составляющая – это решение соответствующего однородного уравнения.

.

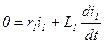(3.4.6)

Если фаза включения такова, ч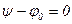то , то 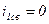и переходного режима нет;

Если 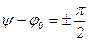, то в момент включения 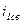достигает своего максиму .

В этом случае 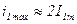и достигает этого значения через 0, 5 периода.

Из этого следует, что свободный ток возникает тогда, когда в момент включения вынужденный ток не проходит через 0. Свободный ток – это результат реакции инерционной цепи на импульс, стремящийся изменить её режим. Этот свободный ток сглаживает переход к новому режиму, не допуская мгновенного изменения тока, которое невозможно в инерционной цепи.

Внезапное короткое замыкание

Короткое замыкание – это такой режим, при котором вторичные зажимы замыкаются накоротко. Короткое замыкание может быть установившееся (постепенное повышения U), об этом режиме уже говорили, и внезапное, возникающее при различных неисправностях в электрических сетях: ошибочное действие персонала, повреждения изоляции: механический или электрический пробой. Замыкание в этом случае происходит не на пониженном, а на номинальном (полном) напряжении сети.

Схема замещения в этом случае такая же, как в условиях установившегося к. з., то есть первичное напряжение приложено к Z_к.Согласно схеме переходный процесс описывается идентичным дифференциальным уравнением:

.

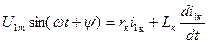(3.4.17)

Так же, как и в предыдущем случае, решение имеет вид:

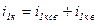,	(3.4.18)
,	(3.4.19)
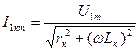,	(3.4.20)
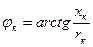,	(3.4.21)
Если трансформатор работал под нагрузкой перед коротким замыканием,:
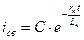,	(3.4.22)

где C находится из начальных условий

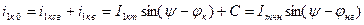
	(3.4.23)
	(3.4.24)
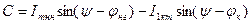
	(3.4.25)

отсюда

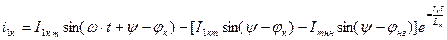
(3.4.26)

Выражение в квадратных скобках – это амплитуда свободной составляющей тока, чем она больше, тем больше пиковое значение тока.

Проанализируем влияние нагрузки на С. Поскольку 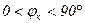, т. е. ток короткого замыкания имеет индуктивный характер, то если 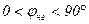, т. е. нагрузка тоже индуктивная, то слагаемые в скобках вычитаются. Т. е. индуктивная нагрузка снижает бросок тока внезапного короткого замыкания. А емкостная нагрузка, наоборот, увеличивает С и, следовательно, бросок тока.

Если 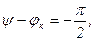то при холостом ходе (режим этот более опасен, чем режим R-L)

(3.4.27)

Максимальное значение тока достигается при ω t = π или через 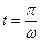после начала к. з. Этот ток называют ударным

,

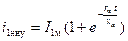(3.4.28)

а выражение в скобках – ударным коэффициентом

,

(3.4.29)

который показывает, во сколько раз ударный ток больше амплитуды установившегося тока короткого замыкания. .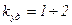

Для мощность трансформаторов 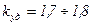для малых –

Действия токов короткого замыкания

Хотя короткое замыкание длится недолго, но температура его обмоток может достигнуть значений, угрожающих целости изоляции.

Допустимой считают температуру 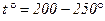и время её достижения определяют по формуле

,

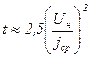(3.4.30)

где j – средняя плотность тока.

Обычно сек, за это время защита отключает повреждение.

Рисунок 3.4.2 – Механические усилия при коротком замыкании

Поскольку токи в обмотках, 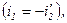то внутренняя обмотка сжимается, а внешняя растягивается. Поскольку 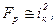то сила пульсирует с частотой 100 Гц и имеет один знак, что может привести к разрушению обмотки.

Аксиальные силы – результат между – виткового взаимодействия каждой обмотки, они стремятся сжать обмотку.