Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Расчет параметров критериального уравнения

Для установления функциональной связи между числам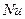и и в виде зависимости необходимо найти значения коэффициентов .

Наиболее обоснованным и широко распространенным в практике научных исследований видом аппроксимации опытных данных является метод " наименьших квадратов", связанный со статистическим законом распределения случайных ошибок эксперимента.

Сущность метода заключается в том, что он обеспечивает минимальное значение суммы квадратов отклонений опытных точек по вертикали от расчетной зависимости, описывающей экспериментальные данные.

Применим данный метод для окончательной обработки результатов экспериментов, используя значение показателя степени при комплексе . (Следует заметить, что , как правило, значительно меньше и погрешность в определении не сказывается существенно на результатах расчетов чисел .).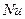

Прологарифмируем исходное выражение и представим его следующим образом:

;

;

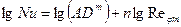Обозначив , получим:

;

При известных значениях все опытные данные можно обобщить в координатах .

Исходя из среднеарифметических значений и , расчетные соотношения для коэффициентов имеют вид:

;

;

где ; ; - число опытов.

Расчет для одной (1-ой) точки.

1) ;

2) ;

3) ;

4) ;

5) ;

Результаты промежуточных расчетов экспериментальных точек представлены

в Таблице 4.

Таблица 4. Статистическая обработка опытных данных

Номер опыта						Сумма
	2, 1943	1, 9841	2, 0612	2, 0078	1, 9135	10, 1609
	4, 8150	3, 9367	4, 2486	4, 0313	3, 6616	20, 6932
	5, 0399	4, 9791	4, 8935	4, 8180	4, 6479	24, 3784
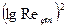
	25, 4006	24, 7910	23, 9462	23, 2132	21, 6030	118, 9540
	11, 0591	9, 8791	10, 0865	9, 6737	8, 8939	49, 5923
	0, 1621	-0, 0481	0, 0290	-0, 0244	-0, 1187	-0, 0001
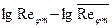
	0, 1642	0, 1034	0, 0178	-0, 0577	-0, 2278	-0, 0001
	0, 0266	-0, 0050	0, 0005	0, 0014	0, 0270	0, 0505
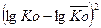
	0, 0263	0, 0023	0, 0008	0, 0006	0, 0141	0, 0441
	0, 0270	0, 0107	0, 0003	0, 0033	0, 0519	0, 0932

6) ;

7) ;

8) ;

9) ;

10)

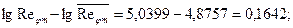
11) ;

12) ;

13) ;

;

;

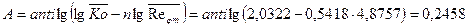График зависимости представлена на Рисунке 5 Приложения.