
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Расчет на образование трещин, нормальных к продольной оси
|
|
Выбор категории трещиностойкости зависит от условий эксплуатации. Панель эксплуатируется в закрытом помещении без агрессивной среды, поэтому относим ее к 3 категории трещиностойкости – допускается образование продолжительных и непродолжительных трещин с ограниченной шириной раскрытия.
Трещины, нормальные к продольной оси, не образуются, если соблюдается следующее условие:

где М – момент от полной нормативной нагрузки;
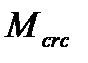 – момент, который может воспринимать сечение перед образованием трещин,
– момент, который может воспринимать сечение перед образованием трещин,
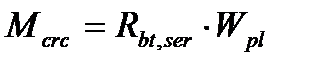 , (31)
, (31)
где  – сопротивление бетона растяжению для расчета по II группе предельных состояний,
– сопротивление бетона растяжению для расчета по II группе предельных состояний,
 – упруго-пластический момент сопротивления,
– упруго-пластический момент сопротивления,
 , (32)
, (32)
где γ – коэффициент, учитывающий влияние неупругих деформаций бетона в растянутой зоне, зависит от формы сечения, для двутаврового сечения γ = 1, 75.
 см³
см³
 кН·м
кН·м
67, 93 > 19, 15  , условие не выполняется.
, условие не выполняется.
2.6.3 Расчет на раскрытие трещин, нормальных к продольной оси
Нормативная величина продолжительной ширины раскрытия трещин:
 мм
мм
Нормативная величина непродолжительной ширины раскрытия трещин:
 мм
мм
Согласно СНиП ширина раскрытия трещин определяется:
 , (33)
, (33)
где  – коэффициент продольного армирования,
– коэффициент продольного армирования,
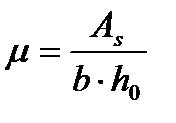 (34)
(34)

 – коэффициент, учитывающий напряженное состояние элементов, для изгибаемых элементов
– коэффициент, учитывающий напряженное состояние элементов, для изгибаемых элементов 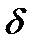 = 1,
= 1,
 – коэффициент, учитывающий вид и класс арматуры,
– коэффициент, учитывающий вид и класс арматуры,  =1;
=1;
 – коэффициент, учитывающий продолжительность действия нагрузки, при непродолжительном действии
– коэффициент, учитывающий продолжительность действия нагрузки, при непродолжительном действии  = 1, при продолжительном действии:
= 1, при продолжительном действии:
 (35)
(35)

 – напряжение в растянутой арматуре,
– напряжение в растянутой арматуре,
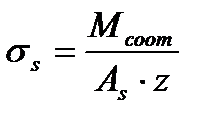 (36)
(36)
где Мсоот – изгибающий момент от соответствующей нагрузки,
z – плечо для соответствующего момента,
 (37)
(37)
где  – коэффициент, определяемый как
– коэффициент, определяемый как
 (38)
(38)

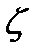 – коэффициент, определяемый как
– коэффициент, определяемый как
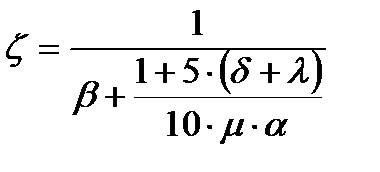 (39)
(39)
где  – величина, определяемая как
– величина, определяемая как
 – величина, определяемая как
– величина, определяемая как
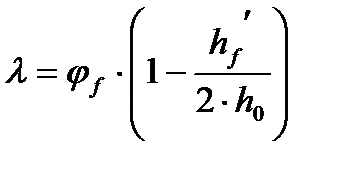 (40)
(40)

 – коэффициент, для тяжелого бетона
– коэффициент, для тяжелого бетона 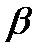 = 1, 8.
= 1, 8.
Определим продолжительную ширину раскрытия трещины от действия постоянной и длительной нагрузки  .
.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение


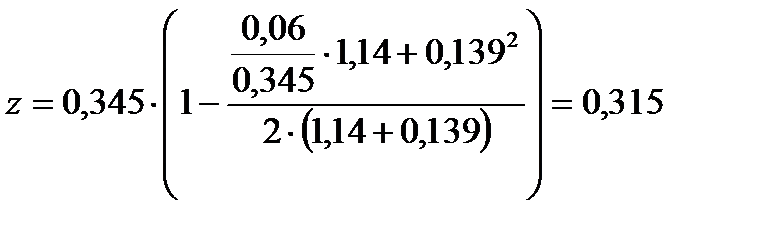 м
м
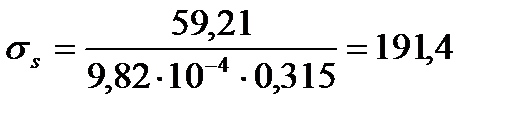 МПа
МПа
 мм
мм
 ,
, 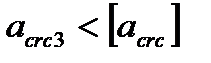 , условие выполняется.
, условие выполняется.
Определим непродолжительную ширину раскрытия трещин
 , (41)
, (41)
где  – непродолжительная ширина раскрытия трещин от действия полной нормативной нагрузки,
– непродолжительная ширина раскрытия трещин от действия полной нормативной нагрузки,
 – непродолжительная ширина раскрытия трещин от действия постоянной и длительной нагрузки.
– непродолжительная ширина раскрытия трещин от действия постоянной и длительной нагрузки.
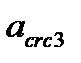 – продолжительная ширина раскрытия трещин от действия постоянной и длительной нагрузки
– продолжительная ширина раскрытия трещин от действия постоянной и длительной нагрузки
Определим непродолжительную ширину раскрытия трещин от действия полной нормативной нагрузки
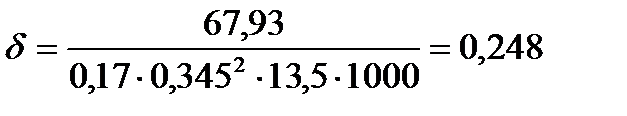

 м
м
 МПа
МПа
 мм
мм
Определим непродолжительную ширину раскрытия трещин от действия постоянной и длительной нагрузки


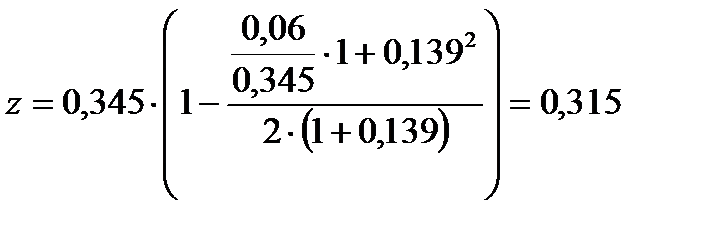 м
м
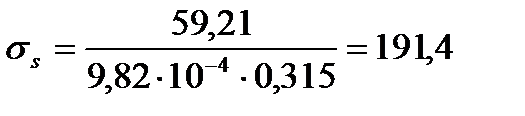 МПа
МПа
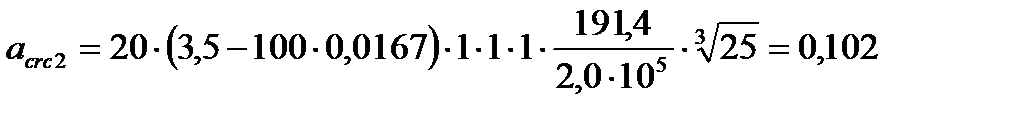 мм
мм
 мм
мм
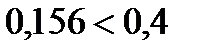 ,
,  , условие выполняется.
, условие выполняется.
2.6.4 Расчет на образование трещин, наклонных к продольной оси
Трещины, наклонные к продольной оси, не образуются, если выполняется условие:
 , (42)
, (42)
где  – внешняя поперечная сила от действия полной нормативной нагрузки,
– внешняя поперечная сила от действия полной нормативной нагрузки,  кН,
кН,
 – минимальная поперечная сила, воспринимаемая бетоном при образовании трещин:
– минимальная поперечная сила, воспринимаемая бетоном при образовании трещин:
 (43)
(43)
 кН
кН
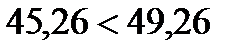 ,
,  , условие выполняется, следовательно, трещины, наклонные к продольной оси, не образуются.
, условие выполняется, следовательно, трещины, наклонные к продольной оси, не образуются.
2.6.5 Расчет по деформациям
Прогиб определяется по следующей формуле:
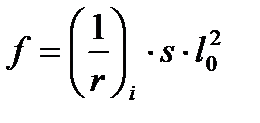 , (44)
, (44)
где  – кривизна,
– кривизна,
 – коэффициент, учитывающий характер нагрузки, для равномерно распределенной нагрузки
– коэффициент, учитывающий характер нагрузки, для равномерно распределенной нагрузки 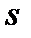 =
=  .
.
Если образуются трещины нормальной продольной оси, то непродолжительная величина прогиба определяется по формуле:
¦ = ¦1 – ¦2 + ¦3, (45)
где ¦1 – непродолжительный прогиб от действия полной нормативной нагрузки;
¦2 – непродолжительный прогиб от действия постоянной и длительной нагрузки;
¦3 – продолжительный прогиб от действия постоянной и длительной нагрузки.
Кривизна на участке с трещинами определяется:
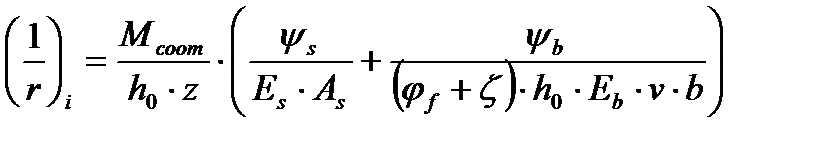 , (46)
, (46)
где  – коэффициент, учитывающий работу растяжения бетона на участке с трещинами:
– коэффициент, учитывающий работу растяжения бетона на участке с трещинами:
 , (47)
, (47)
где  – коэффициент, при продолжительном действии нагрузки
– коэффициент, при продолжительном действии нагрузки  = 0, 8, при непродолжительном действии нагрузки
= 0, 8, при непродолжительном действии нагрузки  = 1, 1,
= 1, 1,
 – параметр, определяемый как
– параметр, определяемый как
 (48)
(48)
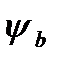 – коэффициент, учитывающий влияние сжатых полок,
– коэффициент, учитывающий влияние сжатых полок,  = 0, 9,
= 0, 9,
 – коэффициент, учитывающий длительность действия нагрузки, при продолжительном действии нагрузки
– коэффициент, учитывающий длительность действия нагрузки, при продолжительном действии нагрузки  = 0, 15, при непродолжительном действии нагрузки
= 0, 15, при непродолжительном действии нагрузки  = 0, 45,
= 0, 45,
Должны выполняться условия:
¦ ≤ 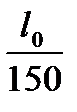 мм,
мм,
¦3£ 25 мм.
Определим продолжительный прогиб от действия постоянной и длительной нагрузки.

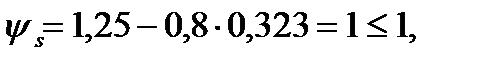
z = 0, 315 м (из расчета продолжительной ширины раскрытия трещин, нормальных к продольной оси).
φ f = 1, 14 (из расчета на раскрытие трещин, нормальных к продольной оси).
ζ = 0, 139 (из расчета продолжительной ширины раскрытия трещин, нормальных к продольной оси).
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
 м-1
м-1
 , условие выполняется.
, условие выполняется.
Непродолжительный прогиб от действия полной нормативной нагрузки.


z = 0, 315 м (из расчета непродолжительной ширины раскрытия трещин, нормальных к продольной оси, от действия полной нормативной нагрузки).
ζ = 0, 137 (из расчета непродолжительной ширины раскрытия трещин, нормальных к продольной оси, от действия полной нормативной нагрузки).
 м-1
м-1
 м.
м.
Определим непродолжительный прогиб от действия постоянной и длительной нагрузки.

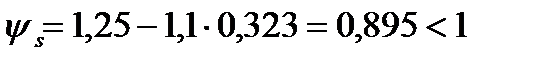
z = 0, 315 м (из расчета непродолжительной ширины раскрытия трещин, нормальных к продольной оси, от действия постоянной и длительной нагрузки).
ζ = 0, 139 (из расчета непродолжительной ширины раскрытия трещин, нормальных к продольной оси, от действия постоянной и длительной нагрузки)
 м-1
м-1
 м
м
Непродолжительная величина прогиба:

 м
м
0, 0194 < 0, 0408, условие выполняется.
2.7 Расчет панели на монтажные нагрузки
Для монтажа и транспортировки панели в ней предусматривают четыре монтажные петли из арматуры класса А-I.

Рисунок 9 – Расположение монтажных петель
Выполняем проверку панели на отрицательные моменты:
 , (49)
, (49)
где kd – динамический коэффициент, kd = 1, 6.
 кН/м
кН/м
Изгибающий момент на консоли:
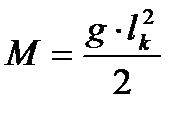 (50)
(50)
 кН·м
кН·м
Площадь сечения арматуры, необходимая для восприятия момента:
 (51)
(51)
 см²
см²
По данной площади принимаем 1 стержень A-I d = 6 мм с Asф = 0, 283 см2.
Рассчитываем монтажные петли. Считаем, что при подъёме вся нагрузка передаётся на две петли. Усилие на одну петлю:
 (52)
(52)
 кН(53)
кН(53)
 (54)
(54)
 см2(55)
см2(55)
Принимаем 4 стержня из арматуры класса A-I d = 12 мм с площадью сечения одного стержня Asф = 1, 131 см2.
3. Расчет и конструирование многопролетного неразрезного ригеля.
3.1 Определение размеров ригеля
Ригель прямоугольного сечения
Зададимся размерами сечения ригеля:
 мм(56)
мм(56)
 мм, из практики проектирования принимаем
мм, из практики проектирования принимаем  мм(57)
мм(57)

Рисунок 10 – Поперечное сечение ригеля
3.2. Сбор нагрузок на ригель.
Постоянная нагрузка на ригель:
 , (58)
, (58)
где  – нагрузка от собственного веса ригеля,
– нагрузка от собственного веса ригеля,
 , (59)
, (59)
где  – площадь поперечного сечения ригеля,
– площадь поперечного сечения ригеля,
 м² (60)
м² (60)
 кН/м
кН/м
 кН/м
кН/м
Временная нагрузка:
 (61)
(61)
 кН/м
кН/м

Рисунок 11 – Сбор нагрузок на ригель
3.3 Характеристики материалов
Бетон В25 Rb = 14, 5 МПа;
Rbt = 1, 05 МПа;
Ев = 3, 0·104 МПа
γ в2 – коэффициент, учитывающий длительность нагрузки; γ в2 =0, 9
Rb = 14, 5 · 0, 9 = 13, 05 МПа;
Rbt = 1, 05 · 0, 9 = 0, 945 МПа.
Арматура А-II Rs = 280 МПа;
Rsc = 280 МПа;
Еs = 2, 1·105 МПа
|
|
