Влияние и учет реальной формы частиц

Реальные частицы породного шлама не имеют идеальной сферической формы. Чем больше форма частицы отличается от сферической, тем сильнее нарушается симметрия обтекания, тем большее сопротивление встречает частица при движении в среде. Критическая скорость частиц неправильной формы всегда меньше скорости шаров равных объема и массы в равных условиях. По нашим наблюдениям во время полевых работ по бурению с продувкой, расчет требуемой скорости восходящего потока воздуха, проведенный по законам для шаровидных частиц, дает завышенные значения.

Эксперименты по изучению влияния формы частиц на критическую скорость проводились многими исследованиями. Только для тел ряда правильных геометрических форм (куб, тетраэдр, октаэдр и др.) с гладкой поверхностью были установлены четкие зависимости коэффициента сопротивления от критерия Рейнольдса, принимавшиеся во внимание при расчетах. Неправильные формы бесконечно разнообразны, что усложняет задачу. Многочисленными исследованиями, в особенности обширными и тщательными экспериментами Р. Ричардса и затем П. В. Лященко, доказано, что законы движения шара в среде вполне применимы для расчета движения тел неправильной формы, при использовании найденных на основании опыта поправочных коэффициентов.

В настоящее время частицы неправильной формы условно делят на округленные (окатанные), угловатые (кубоподобные), удлиненные (продолговатые) и плоские (пластинчатые). Большое влияние оказывает фактор субъективности при оценке формы частицы. Так, Риттингер, Успенский, Лобаев и другие не выделяют угловатую форму в отдельную группу, Пернолет и Грэй не признают угловатых и удлиненных форм, Месснер для всех форм рекомендовал общий средний коэффициент к скорости витания 0, 75.

Существуют расхождения и в том, к какой из указанных групп отнести зерна того или иного минерала. Так, форму зерен каменного угля относят к продолговатой, угловатой, угловато-округленной и даже к округленной, кварца - к округленной, угловатой, продолговатой и пластинчатой. Нет оснований заранее приписывать породам и минералам определенную форму зерен. Тем более что на нее оказывает влияние процесс разрушения породы и транспортирования шлама. Только из наблюдений в конкретных условиях можно отнести частицы образующегося при бурении шлама к той или иной форме.

Выделение четырех неправильных форм частиц не вполне оправдано. Между округленной (окатанной) и угловатой (кубоподобной) формами нет принципиальной разницы. Если при плоской (пластинчатой) форме один из размеров существенно меньше, а при удлиненной (продолговатой) больше двух других, то при округленной и угловатой формах все три размера близких между собой. Четких критериев различия нет, и речь может идти только о степени окатанности. Целесообразно объединить обе эти формы под названием «компактной» («изометрической»)

За характерный размер частицы неправильной формы при расчете критической скорости принимают так называемый эквивалентный диаметр, т. е. диаметр шара, эквивалентного данной частице по объему и массе. За линейный размер частицы принимают средний размер ячеек двух сит, между которыми отобран данный класс частиц.

Поправочные коэффициенты формы предлагались многими исследователями либо в виде множителя к коэффициенту сопротивления, либо непосредственно к критической скорости, имелись конкретные значения для каждой определенной формы.

Попытка предложить аналитическое выражение критической скорости для частиц любой формы предпринята В. В. Алексеевым; и Э. Риосом. Приравнивая выражения для движущей силы веса частицы в среде и силы сопротивления среды действующей на миделевое (наибольшее) сечение частицы неправильной формы авторы получают формулу, в соответствии с которой критическая скорость обратно пропорциональна «диаметру заменяющего шара» , вычисляемого как диаметр круга, по площади равного миделевому сечению частицы неправильной формы. Входящий в ту же формулу коэффициент сопротивления определяется для эквивалентного частице шара по номограмме П. В. Лященко. Естественно чем сильнее реальная форма частицы отличается от сферической, тем больше 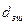и тем ниже критическая скорость. Но этот искусственный прием не позволяет учесть влияние реальной формы частицы на критическую скорость и поэтому, поскольку от формы частицы зависимости механизм обтекания, для каждой отдельной формы в координатах , существует совершенно самостоятельная опытная кривая, что показано, например П. В. Лященко.

В табл. 3.1 сведены опытные значения коэффициента формы , полученные рядом исследователей и представленные в случаях в виде поправочных множителей к критической скорости для шара. Значения коэффициентов у разных авторов различны. Нет оснований отдать предпочтение кому-либо из авторов и вместе с тем нельзя пренебречь результатами специальных исследований, проведенных каждым из них. Значительно большую определенность вносит рассмотрение средних значений каждой формы частиц. Прежде всего, почти полное совпадение средних значений для округленной и угловатой форм подтверждает справедливость их объединения в одну «компактную» форму.

Для проверки и уточнения имеющихся данных экспериментально исследовалось свободное падение стеклянных шариков восьми классов крупности и минеральных частиц трех основных форм и трех классов крупности в жидкости повышенной плотности. На рис. 3.1 графически представлены в логарифмической шкале опытные зависимости между коэффициентом сопротивления по Рэлею и параметром Рейнольдса Re для трех основных форм частиц, а также для стеклянных шариков, и расчетная кривая для идеальных шаров, вычисленная по формуле

.

Каждая из опытных точек для частиц неправильной формы является результатом - 40, а для стеклянных шариков - 20 отдельных замеров. Кривые построены интерполированием.

Таблица 2.1