Основные понятия теории вероятности и математической статистики

ИСХОДНАЯ ИНФОРМАЦИЯ ДЛЯ МОДЕЛИРОВАНИЯ

В данном разделе освещаются вопросы, связанные со сбором исход­ной информации для моделирования и ее обработкой.

ВИДЫ ИНФОРМАЦИИ

Информация для моделирования носит разнообразный характер – детерминированная и случайная, нормативная и расчетная, достоверная и недостоверная, репрезентативная и нерепрезентативная, независимая от деятельности человека и зависимая (изменяющаяся), значимая (ценная) и незначимая, производственная и природная, экономическая и техническая и так далее. Каждый из перечисленных видов информации требует своих подходов для сбора и обработки. Проще всего оперировать с детерминиро­ванной технико – экономической информацией, отраженной в экономико – бухгалтерской отчетности предприятий. Это различные стоимостные показатели – себестоимость, прибыль, приведенные затраты и другие – на валке, обрезке сучьев, трелевке, погрузке, раскряжевке, то есть по операциям и в целом по всему циклу лесозаготовительного производства; временные показатели – коэффициент использования машин и рабочего времени – и прочие. Однако при сборе подобной информации следует обратить особое внимание на ее достоверность – правильность и адекватность представления реальности, – ибо готовят такую информацию люди, которым свойственны различные ошибки.

Наиболее трудоемок процесс получения информации, характери­зующей предмет труда, природно – производственные условия, надежность работы механизмов, колебания их производительности, то есть информа­ции случайного – стохастического или статистического – характера. Более подробно с основными понятиями случайной величины, законами ее рас­пределений, конкретными описаниями отраслевой информации можно познакомиться в [3, 13, 26-31]. Последующие подразделы представляют способы получения достоверной стохастической информации для модели­рования объектов лесозаготовок.

ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТИ И МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ

Для дальнейшего правильного понимания сущности излагаемого ма­териала рассмотрим некоторые понятия теории вероятностей и математи­ческой статистики, более подробно с которыми можно ознакомиться в [28— 30], а также в ГОСТ Р 50779.10-2000 (ИС03534.1-93) «Статистические методы. Вероятность и основы статистики. Термины и определения».

Ключевым понятием теории вероятностей является событие. Собы­тия можно подразделить на три вида: достоверные, невозможные и слу­чайные. Достоверным называют событие, которое обязательно произойдет, если будет иметь место определенная совокупность условий. Невоз­можным называют такое событие, которое при определенной совокупно­сти условий не может произойти ни при каком повторении испытаний. Случайным называется всякое событие, которое в результате опыта при осуществлении определенной совокупности условий может произойти или не произойти. Случай – весьма загадочное явление внезапного появления или непоявления, не позволяющее проникнуть в сущность его самого. Однако физическую величину, присущую тому или иному случайному событию, мы вполне осознаем.

Например, если в арендуемых участках лесного фонда лесозаготови­тельного предприятия полностью отсутствуют насаждения березы, то по­лучение березового фанерного кряжа следует рассматривать как невоз­можное событие. Увеличение потребляемой энергии на один рез при уве­личении диаметров распиливаемых бревен является достоверным событи­ем. Поломка станка в течение данной рабочей смены является случайным событием: она может быть, а может и не быть.

Случайной величиной х называется величина, которая в результате опыта может принять то или иное значение, причем неизвестно заранее - какое именно. Случайная величина содержит множество различных численных значений. Примеры случайных величин: 1) количество сучьев на дереве; 2) уменьшение (сбег) диаметра по длине ствола; 3) время цикла лесообрабатывающего станка; 4) скорость лесовозного автомобиля в каждом рейсе; 5) количество включений раскряжевочной пилы в единицу времени.

Случайные величины, принимающие только отделенные друг от друга значения, которые можно заранее перечислить, называются дискретными случайными величинами. Случайные величины, возможные значения которых непрерывно заполняют некоторый промежуток, называются непрерывными величинами.

Возможность появления случайного события характеризуется вероятностью. Вероятность события есть численная мера степени объективной возможности этого события. Часто вероятность определяют как отношение возможного числа случаев Z _n при которых событие А появляется, к числу всех возможных случаев Z, то есть

P(A)=Z _n /Z.

Вероятность любого события А подчинена условию 0 Р(А) 1, то есть вероятность случайного события – положительное число, заключен­ное между нулем и единицей. Иногда значения вероятностей выражаются в процентах. Чем больше вероятность события, тем чаще оно наступает. Если вероятность события очень мала, практически можно считать его появление при единичном испытании невозможным. Вероятность достоверного события равна единице, невозможного нулю. Практически невозможным называется событие, вероятность которого весьма близка к нулю. Все практическое применение теории вероятностей основывается на существовании практически достоверных и практически невозможных событий.

От вероятности события следует отличать его частость — относи­тельную частоту, статистическую вероятность. Это оценка вероятности из практики по факту происшедшего, в отличие от вероятности, как теорети­ческого понятия, определяемой из умозаключения о возможности. Если проведена серия опытов, в каждом из которых могло появиться или не появиться некоторое событие А, то частостью события А в данной серии опытов называется отношение числа опытов, в которых появилось событие А, к общему числу произведенных опытов. При небольшом числе опытов частость события носит в значительной мере случайный характер и может заметно изменяться от одной группы опытов к другой. При увеличении числа опытов относительная частота событий проявляет тенденцию к ста­билизации, приближаясь с незначительными колебаниями к некоторой средней, постоянной, величине. Математическую формулировку этого свойства «устойчивости частот» впервые дал Я. Бернулли в своей теореме, которая представляет собой простейшую форму закона больших чисел. Им доказано, что при неограниченном увеличении числа однородных незави­симых опытов с практической достоверностью можно утверждать, что относительная частота события будет сколь угодно мало отличаться от его вероятности в отдельном опыте.

Несколько событий называются несовместными в данном опыте, ес­ли никакие два из них не могут появиться вместе. Событие А называется независимым от события В, если вероятность события А не зависит от того, произошло событие В или нет. Событие А называется зависимым от собы­тия В, если вероятность события А меняется в зависимости от того, про­изошло событие В или нет. Вероятность суммы двух или более несовмест­ных событий равна сумме вероятностей этих событий – теорема сложения вероятностей. Сумма вероятностей противоположных событий равна еди­нице. Вероятность появления двух событий равна произведению вероятности одного из них на вероятность другого, вычисленную при условии, что первое имело место. Вероятность одновременного появления независимых событий равна произведению вероятностей этих событий.

Одной из основных задач в изучении случайных величин являются не только установление возможных значений, но и оценка вероятности их появления. Методами решения этой задачи и обработки опытных данных занимается математическая статистика. Ниже дается краткое изложение основных понятий математической статистики.

Результаты наблюдений за тем или иным объектом лесозаготовок - сортименты, хлысты, пучки и плоты, автопоезда и пр., - получившие численные значения в виде случайной величины х_i, называются выборкой, или выборочной совокупностью.

Пусть выборочная совокупность состоит из n однородных единиц – сортименты, хлысты и так далее. Число п является объемом совокупности, или выборки. Единицы совокупности х_i, могут принимать различные чис­ленные значения, причем некоторые значения для дискретной случайной величины могут повторяться п_i раз. Те величины, которые принимают одинаковые численные значения и повторяются n_i раз, называют вариан­тами. Изменение случайной величины х_i при переходе от одного варианта к другому называется вариацией, или рассеянием.

Различают, как отмечалось, дискретные и непрерывные случайные величины. Дискретной является та величина, единицы совокупности кото­рой принимают только целочисленные значения, и измеряется она, как правило, в штуках - количество сортиментов в пачке, сучьев на дереве, валочных машин на лесосеке и так далее. Непрерывной случайной величи­ной называется та, единицы совокупности которой могут принимать любые непрерывные значения в выборке, и измеряется она обычно в объемных, м³, временных, массовых и других подобных единицах.

Число случаев появления (встречаемости) того или иного варианта для дискретной случайной величины называется частотой. Для непрерывной случайной величины частотой называется число случаев попадания ее в заданный интервал.

Упорядочивание вариантов случайной величины в порядке возраста­ния с одновременным определением частот п_i для каждого значения х_i приводит к построению статистического распределения выборки (ряда распределения)

х₁, х₂, х₃,..., х_i,..., х_k

n₁, n₂, n₃,.., n_i, …, n_k,, (2.1)

где k – количество вариантов.

Для непрерывной случайной величины строится интервальный ряд распределения посредством разбиения выборки на k не пересекающихся интервалов, границами которых служат числа x₀, х₁, х₂, х₃,..., х_i,..., х_k. Количество значений n_i, случайной величины х_i, попавшей в полуокрытый интервал (x_{i - 1} , x_i), для которого х_i-1 х< х_i, называется частотой i -го интервала.

Отношение частоты варианта для дискретной или интервала для непрерывной случайных величин к объему выборки называется частостью.

Частость характеризует относительную частоту появления i -го ва­рианта или относительную частоту попадания случайной величины в i -й интервал и определяется по выражению

ω _i = n_i/п. (2.2)

При увеличении n до бесконечности величина ω _i приближается к ве­роятности p_i.

Сумма всех частот равняется объему совокупности

n₁+п₂ +...+п_i+...+п_k =Σ n_i= п. (2.3)

Сумма всех частостей равняется единице:

ω ₁ + ω ₂+…+ ω _i+…+ ω _k = Σ ω _i=1 (2.4)

Дискретные ряды распределения интерпретируются графически по­средством многоугольников распределения, а непрерывные – с помощью гистограмм. Подробно о способах их построения см. в [29].

Практическое представление изложенных понятий иллюстрируется на примере следующей неупорядоченной выборки. Часто данные наблю­дения поступают в распоряжение исследователя в виде неупорядоченного ряда чисел. Так, время раскряжевки х_i каждого последовательно посту­пающего хлыста на установке типа JIO-15C на лесопромышленном складе (в течение непрерывного отрезка времени смены) характеризуется сле­дующими данными: 32, 52, 60, 54, 82, 54, 86, 77, 105, 77, 75, 107, 162, 164, 54, 50, 57, 62, 47, 82, 52, 80, 114. Число измерений (объем выборки) n = 23, а суммарная продолжительность измерений Σ x_i = 1783с.

Расположение вариантов в порядке возрастания или убывания при­знака называется ранжированием ряда. Оно позволяет сопоставить отдельные результаты наблюдения, определить размах между наибольшим и наименьшим значениями. В рассматриваемом примере размах вариации – разность между наибольшим и наименьшим значениями – составит 164-32=132 с. Средняя арифметическая продолжительность цикла – оценка матожидания – равна частному от деления суммы всех измерений на число измерений:

t₀ =Σ x_i /n =1783/23=77, 5 с.

Если бы число опытов при одинаковых условиях можно было повто­рять до бесконечности, то, разделив сумму всех вариантов на число измерений, получили бы математическое ожидание этой величины. При увеличении числа опытов среднее значение величины стремится к ее математическому ожиданию. Среднее значение не характеризует полностью случайную величину и не дает возможности определить степень отклонения ее отдельных значений относительно среднего значения. Мерой рассеивания случайной величины является дисперсия, равная сумме квадратов отклонений значений случайной величины х_i от их среднего арифметического значения (математического ожидания) t₀, деленной на число измерений п. Оценка дисперсии в данном примере равна

S²=Σ (x_i-t₀)²/n= 25348/23=1100 с².

Если оценка дисперсии обозначается S², то дисперсия в теории веро­ятности обозначается σ ². Аналогично обозначается среднеквадратическое отклонение – σ.

Оценка среднеквадратического отклонения (СКО) равна

S = 33, 2 с.

Относительной мерой разброса значений случайной величины явля­ется коэффициент вариации, который равен отношению среднеквадратического отклонения к среднему значению:

V=S /t₀ =33, 2/77, 5=0, 428

Случайная величина будет полностью описана с вероятностной точки зрения, если задано ее распределение, т. е. указано, какой вероятностью обладает каждое из событий. Этим мы устанавливаем так называемый закон распределения случайной величины. Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между значениями случайной величины и соответствующими им вероятностями. Одной из форм закона распределения является функция распределения - интегральный закон распределения, – показывающая вероятность того, что значения случайной величины меньше любого произвольного значения (числа). Функция распределения является самой универсальной характеристикой случайных величин. Она существует для всех случайных величин – как дискретных, так и непрерывных. Функция распределения является неубывающей функцией своего аргумента и существует от - 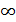до + .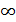

Вероятность нахождения значений случайной величины в каком- либо интервале равна разности между значениями функции распределения при большем и меньшем пределах аргумента (интервала). Вероятность того, что значения случайной величины будут больше какого-либо числа, равна разности между единицей и соответствующим значением функции.

Производная функции распределения называется плотностью распределения – дифференциальным законом распределения. Плотность распределения существует только для непрерывных случайных величин. Она является неотрицательной функцией. Интеграл в бесконечных пределах от плотности распределения равен единице.

Графически теоретические функции и плотность распределения не­прерывных случайных величин изображаются плавными кривыми – кривые распределения, а закон и функция распределения дискретных случайных величин – в виде ломаных линий.

При большом числе наблюдений (порядка сотен) простая статистическая совокупность или вариационный ряд перестают быть удобной формой записи статистического материала. Статистический ряд непрерывной случайной величины оформляется графически в виде гистограммы. Гистограмма строится следующим образом. По оси абсцисс откладывают разряды – интервалы группирования значений случайной величины. Затем подсчитывают число измерений, значения которых находятся в данном разряде. На каждом из разрядов, как на основании, строят прямоугольник, площадь которого равна частоте данного разряда. По оси ординат откладывают частоту (вероятность). Полная площадь гистограммы равна единице.

Для предварительного определения ширины разрядов d можно использовать следующую приближенную формулу, предложенную Г.А. Стреджерсом:

d=(x_max-x_min)/(1+3, 322lg n),

где x_max-x_min – размах вариации (разность между наибольшим х_тах и наименьшим x_min значениями);

n - объем выборки;

l+3, 322 lg n – число разрядов (интервалов).

При обработке опытных данных ширину разряда следует округлять до целого числа, а количество разрядов рекомендуют принимать от 10 до 20. Если середины вершин прямоугольников гистограммы последовательно соединить прямолинейными отрезками, то получим ломаную линию, называемую полигоном распределения. Для дискретных случайных величин строят полигон распределения, у которого значения ординат пропор­циональны соответствующим частотам.

При необходимости анализа изменения изучаемой переменной по времени, данные располагают в хронологической последовательности. Последовательность значений какой-либо переменной, наблюдаемой на протяжении определенного периода времени, называют временным рядом. Временной ряд позволяет анализировать ритмичность производства и вы­полнение плана по дням, месяцам.

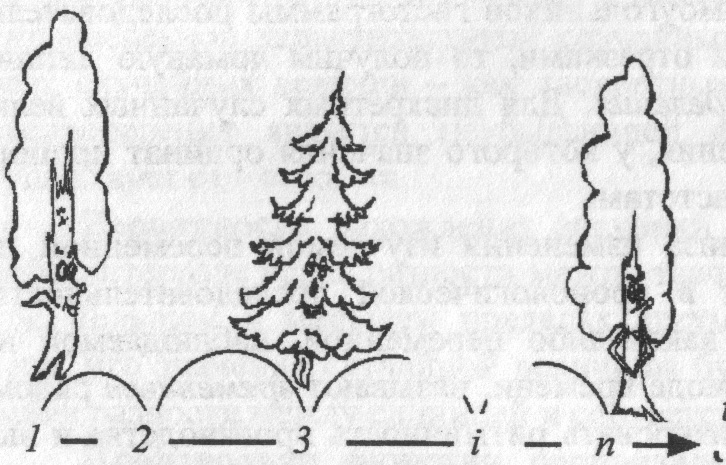
Потоки заявок (требований), поступающих на обслуживание. Они характеризуются интервалами времени (рис. 2.1), разделяющими последовательные поступления заявок на обслуживание, и распределением интервалов. В системах массового обслуживания (СМО) при описании потока заявок используются законы распределения вероятностей, а именно: распределение моментов или интервалов времени поступления заявок (требований). Эти распределения отражают либо индивидуальное (ординарное) поступление и обслуживание заявок (по одной), либо групповое (неординарное) поступление и обслуживание (в этом случае обслуживающая система называется системой с параллельно–групповым обслуживанием, например, пачковая раскряжевка). Например, ординарным потоком будет прибытие автомашин на лесосклад, неординарным будет количество деревьев, доставляемых на погрузочный пункт трелевочной машиной.

Количественно потоки также характеризуются средним числом зая- иок, поступающих в обслуживающую систему в единицу времени, это есть интенсивность поступления заявок l. Обратная величина l(1/l) является средним интервалом времени между поступлениями заявок.

Поток требований может быть регулярным (детерминированным), когда каждое требование поступает через равные промежутки времени, и нерегулярным, когда требования поступают через случайные промежутки времени. Поток может быть стационарным, когда его вероятностные ха­рактеристики (оценки матожидания и дисперсии) не зависят от времени, и нестационарным, когда поведение системы и ее вероятностные характери­стики есть функция времени. Для стационарного потока характерна посто­янная плотность (интенсивность) - среднее число требований в единицу времени. Например, груженые лесовозные машины, ежедневно прибы- вающие на лесопромышленный склад в течение зимнего периода, можно рассматривать как стационарный поток. Однако в течение года интенсивность вывозки автомашинами меняется, и для годового периода этот поток будет нестационарным.

Поток может быть без последействия, то есть с отсутствием памяти, когда требования появляются в последовательные моменты времени независимо друг от друга. Поток событий (заявок), являющийся стацио­нарным, ординарным с отсутствием последействия, называется простейшим, или пуассоновским, потоком.

Поступающий поток характеризуется также емкостью источника, который его создает. Емкость источника, генерирующего заявки на обслуживание, может быть ограниченна – количество заявок на ремонт не может быть больше количества машин и неограниченна – деревья, поступающие в рубку в условиях неистощенной лесосырьевой базы.

Более подробно о потоках лесопромышленных объектов и их харак­теристиках можно прочесть в [3, 13, 15].

Распределение вероятностей случайных величин. Для оценки ве­роятности появления той или иной случайной величины используются описывающие их законы распределения. Наиболее часто встречаются сле­дующие распределения вероятностей дискретных случайных величин: биноминальное, гипергеометрическое, пуассоновское.

Биноминальное распределение вероятностей описывает появление событий, имеющих два противоположных исхода. Например, этими исходами может быть количество исправных и находящихся в ремонте трелевочных тракторов, лесовозных автомобилей, бензо- и электропил. Если вероятность события постоянна и равна р, то вероятность того, что это событие произойдет точно т раз в п повторяющихся испытаниях – закон распределения, – равна

p_m = p^m(1-p)^n-m= ^т (1-р) ^n-т, (2.6)

где – число сочетаний из п по m; m!, n! – факториалы чисел m, n;

n! =1*2*3*…*(n-1)*n.

Рис. 2.1. Графическая интерпретация потока заявок в течение времени

Биноминальное распределение имеет два параметра (характеристики распределения) р и п. Математическое ожидание – среднее значение – случайной величины, распределяемой по биноминальному закону, равно пр, а дисперсия равна (l- p) np.

Гипергеометрическое распределение получается при следующих условиях. Допустим, что в общем объеме совокупности, состоящей из N предметов, М предметов обладают нужным признаком, а (N-M) этим при­знаком не обладают. Если из общего объема выбрать наугад п предметов, то вероятность того, что m предметов среди выбранных обладают нужным свойством, а остальные (п-т) им не обладают, определится по формуле

p_n = / (2.7)

Это распределение отличается от биноминального тем, что изъятый объект обратно в совокупность не возвращают. Гипергеометрическое рас­пределение характеризуется тремя параметрами: 1) объемом совокупности N; 2) объемом выборки п и 3) вероятностью того, что первый отобранный предмет будет иметь нужный признак, M/N.

Математическое ожидание случайной величины, характеризуемой гипергеометрическим распределением, равно nM/N, а дисперсия равна

M(N-M) (2.8)

Одним из наиболее распространенных законов распределения веро­ятностей дискретных случайных величин является закон Пуассона. Вероятность того, что случайная величина m_х примет значение z = О, 1, 2, 3,..., определяется формулой

P_z=e^-a 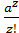(2.9)

где е 2, 7183 - основание натуральных логарифмов;

а -среднее число событий за данный постоянный интервал времени t;

z! - факториал числа z, z! = l*2*3*...*(z– 1) z, a = l t, где l- интенсивность появления событий – среднее количество событий, появляющихся в единицу времени. Вероятность того, что событие за время t не наступит (m_х = 0), равна e^-a.

Закон Пуассона имеет только один параметр а. Математическое ожидание и дисперсия случайной величины, имеющей пуассоновское распределение, равны между собой и равны параметру а. Это равенство среднего значения и дисперсии часто рассматривается как свидетельство или, по крайней мере, как некоторое указание на то, что распределение анализируемой случайной величины следует закону Пуассона. Этот закон является предельным. К нему приближаются распределения многих дискретных случайных величин (потоков) при условии более или менее равномерного воздействия на них большого числа случайных факторов.

В лесозаготовительных процессах чаще могут встречаться следую­щие основные виды распределения непрерывных величин: показательное (экспоненциальное), нормальное, усеченное нормальное, эрланговское, равномерное, размаха.

Показательным законом описывается распределение случайных интервалов времени между наступлением событий, подчиняющихся закону распределения Пуассона. Утверждения о том, что распределение длитель­ности интервалов времени между последовательным появлением событий является показательным (экспоненциальным) или что распределение числа событий за одинаковые интервалы подчиняется закону Пуассона, равно­сильны. Вероятность того, что значения случайной величины, имеющей показательное распределение, будут меньше t (функция распределения), равна P(t)=1–e^-lt. (2.10)

Плотность показательного распределения

P(t)=le^–lt . (2.11)

Обозначения величин расшифрованы ранее. Математическое ожида- ние и среднеквадратическое отклонение равны между собой и равны 1/l. Если промежуток времени, распределенный по показательному закону, уже длился некоторое время, то это никак не влияет на закон распределения оставшейся части промежутка: он также будет показательным.

Распределение Эрланга связано с пуассоновским распределением и получается преобразованием последнего. Если пользоваться терминологи­ей теории массового обслуживания, то можно констатировать, что поток Эрланга получается путем особого преобразования (разрежения) стацио­нарного пуассоновского (простейшего) потока, заключающегося в выбра- сывании некоторых событий из простейшего потока.

Потоком Эрланга К -то порядка называется поток, полученный из простейшего, если сохранить каждое (К +1)-е событие, а остальные исклю­чить. В свою очередь простейший поток можно рассматривать как поток Эрланга нулевого порядка. Функция эрланговского распределения будет иметь вид

(2.12)

Плотность распределения равна

p_k(t)=l(l t)^Кe^–lt/ К! (2.13)

где К = О, 1, 2, 3,... – порядок распределения Эрланга;

l – интенсивность исходного простейшего (пуассоновского) потока; t - интервал времени; е - основание натуральных логарифмов; п - переменная величина, п = О, 1, 2, 3,..., К.

Математическое ожидание случайной величины, распределенной по закону Эрланга, равно (К+1)/l, а дисперсия (К+1)/l ².

При неограниченном увеличении К нормированный поток Эрланга приближается к регулярному потоку с постоянными интервалами между заявками, равными 1/l.

Нормальное распределение, распределение Гаусса – Лапласа, встре­чается в практике наиболее часто. Этот закон является предельным, к ко­торому приближаются другие законы распределения при наличии опреде­ленных условий. Сумма достаточно большого числа независимых (или слабо зависимых) случайных величин, подчиненных каким угодно законам распределения, приближенно подчиняется нормальному закону, и это правило выполняется тем точнее, чем большее количество случайных величин суммируется.

Плотность распределения случайной величины х, соответствующая нормальному закону, равна

Функция распределения равна

Здесь среднее квадратическое отклонение σ и математическое ожидание V являются параметрами распределения;

Ф и - нормированные интегральная и дифференциальная функции Лапласа; π = 3, 141...; е = 2, 7183.

При любых значениях σ и V площадь, ограниченная кривой распределения и осью абсцисс, равна единице. Кривая нормального распределе­нии имеет холмообразный симметричный вид. Если σ оставить постоянной, а V изменить, то кривая распределения сместится вдоль оси абсцисс, не изменяя своего вида. При малых значениях σ кривая нормального рас­пределения принимает иглообразный вид, а при больших становится плос­ковершинной. В пределах V ±σ находится 68, 3 % всех значений случайной величины, подчиняющейся нормальному распределению; в пределах V ±2 σ и V ±3 σ - соответственно, 95, 4 и 99, 7 %. Пределы значений случайной ве­личины могут быть от – 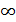до +

Усеченное нормальное распределение получается, если значения случайной величины будут ограничены справа или слева каким-то преде­лом С – точкой усечения. Плотность односторонне усеченного нормально­го распределения

p(x) = (2.16)

Функция такого распределения равна

Р (х)= (2.17)

Параметры распределения – математическое ожидание V и среднее квадратическое отклонение σ – определяются с помощью специальных функций.

Равномерное распределение вероятностей характеризует непрерывные случайные величины, все возможные значения которых лежат в пределах определенного интервала, причем в этих пределах плотность вероятности их постоянна. Плотность распределения равна

р(х) = при а х < b;

р(х) = 0 при а > х > b. (2.18)

О 2 4 6 8 10 X

Рис. 2.2. Плотности различных законов распределения случайных величин: а - непрерывных; б - дискретных

Функция распределения равна:

Р(х) = при а х

Р(х) = 0 при х < а:

Р(х) = 1 при х 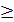b - (2.19)

а и b - нижний и верхний пределы значений случайной величины. Математическое ожидание равно (а +b)/2, а дисперсия (b - a)²/12.

Другие распределения непрерывных случайных величин (см. рис. 2.2) будут пояснены при решении конкретных задач.

Многие практические задачи связаны с нахождением закона распре­деления суммы независимых случайных величин по известным законам распределения слагаемых, то есть с композицией распределений. Если имеются две независимые случайные величины х и у с плотностями рас­пределений, соответственно, p₁ (х) и p ₂(у), то плотность распределения их суммы z=x+у определяется следующим законом композиции:

p(z)= (x) p ₂(z-x) dx. (2.20)

При композиции двух или более независимых случайных величин, подчиненных нормальному закону распределения, также получается нор­мальный закон. Конечное распределение будет иметь дисперсию и математическое ожидание, равные, соответственно, суммам этих величин исходных распределений. Из наиболее распространенных распределений вероятностей, кроме распределения Гаусса, только распределение Пуассона обладает аналогичным свойством.

Композиция двух независимых показательных распределений с оди­наковыми параметрами и плотностями, равными p₁(x)=le^–lx и р₂(у)=l e^—ly дает для z = х + у плотность p(z) = z l² e^{-l z}. (2.21)

При необходимости определить распределение суммы большего количества случайных величин при известных законах их распределения следует прибегнуть к методу последовательной их композиции.