Маршрут

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Маршрут

Граф это множество точек или вершин и множество линий или ребер, соединяющих между собой все или часть этих точек. Вершины, прилегающие к одному и тому же ребру, называются смежными.
Если ребра ориентированы, что обычно показывают стрелками, то они называются дугами, и граф с такими ребрами называется ориентированным графом.
Если ребра не имеют ориентации, граф называется неориентированным.

Две вершины называются смежными, если они соединены ребром. Два ребра называются смежными, если они имеют общую вершину. Матрица смежности графа G с конечным числом вершин n (пронумерованных числами от 1 до n) — это квадратная матрица A размера n, в которой значение элемента a_ij равно числу рёбер из i-й вершины графа в j-ю вершину.

Диаграмма – это один из видов представления графа. Суть метода заключается в визуальном представлении графа. Изображение заключается в представлении на плоскости совокупности точек (вершин) и связывающих их линий (дуг).

Путь в графе — последовательность вершин, имеющая для каждой вершины ребро, соединяющее её со следующей вершиной в последовательности.

Длина маршрута (пути)– количество ребер (дуг) маршрута (пути).

Вес маршрута (пути) –сумма весов ребер (дуг) маршрута (пути).

Замкнутый маршрут (замкнутый путь)– маршрут (путь), у которого первая и последняя вершины совпадают.

Простой маршрут (простой путь) –маршрут (путь) без повторяющихся вершин.

Цепь (орцепь) –маршрут (путь), в котором ребра (дуги) проходятся один раз.

Простая цепь (простая орцепь) –цепь (орцепь) без повторяющихся вершин.

Петля– цепь (орцепь), содержащая один узел и одно ребро (одну дугу).

Неориентированный граф считается связным, если из любой вершины есть путь в любую другую вершину (путь может состоять из любого количества рёбер).

Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer

Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM. SeoHammer делает продвижение сайта прозрачным и простым занятием. Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.

Что умеет делать SeoHammer

— Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.

SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней.

Зарегистрироваться и Начать продвижение

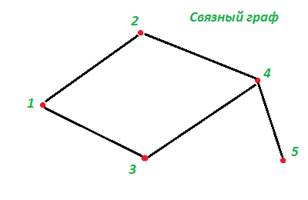
Чтобы граф сnвершинами был связным, он должен иметь не менее (n-1) рёбер.

Если граф имеет не менее(n*n - 3n + 4)/2рёбер, то он гарантированно связный.

Если граф связный, у него обязательно есть вершины степени не менее 2, то есть вершины, каждая из которых имеет не менее двух смежных вершин.

Если граф связный и без циклов (то есть это дерево), то удаление любого ребра приведёт к потере связности.

Несвязный граф состоит из компонент связности. Компонента связности - множество вершин такое, что из любой вершину этого множества есть путь в любую другую вершину этого множества, но ни из какой вершины этого множества нельзя попасть в некоторую вершину вне этого множества. Очевидно, что сумма количеств вершин компонент связности равна количеству вершин графа.

Выбираем некоторую вершину A и помечаем её как посещённую (1), остальные соответственно полагаются ещё не посещёнными (0):

A полагаем текущей вершиной. Дальше действуем следующим образом. Пометка непосещённых смежных вершин: для текущей вершины ищем смежные с ней, ещё не непосещённые, и помечаем их как посещённые.

Пусть у нас оказалось k новопомеченных вершин (на рисунке чуть выше их 3). По очереди выбираем одну из них текущей и рекурсивно выполняем пометку непосещённых смежных с ней вершин. Для текущей вершины не выполняется рекурсия, если у данной вершины нет смежных вершин, которые всё ещё не помечены как посещённые.
Если после таких действий все вершины окажутся помечены как посещённые, граф связный, иначе несвязный.