Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Несимметричные трехфазные системы

Если хотя бы одно из условий симметрии не выполняется, трехфазная цепь работает в несимметричном режиме. Такие режимы при подключении статической нагрузки рассчитываются любым из известных методов расчета линейных электрических цепей с источниками гармонических воздействий. Как правило, падением напряжения на внутреннем сопротивлении генератора пренебрегают и фазные напряжения генератора заменяются соответствующими идеальными источниками ЭДС. Поскольку в трехфазных цепях, помимо значений токов, обычно представляют интерес также величины потенциалов узлов, в большинстве случаев для расчета применяется метод узловых потенциалов.

Если заданны линейные напряжения, удобно рассчитывать трехфазные цепи при соединении фаз нагрузки в треугольни к. Пусть в схеме (см. рис. 1, б) нагрузка несимметрична и . Тогда при известных комплексах линейных напряжений в соответствии с законом Ома фазные токи

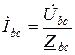; ; . (11)

По найденным фазным токам приемника на основании первого закона Кирхгофа определяются линейные токи:

. (12)

Если к трехфазному генератору, фазы которого соединены звездой (рис. 2), подключен приемник электрической энергии, фазы которого также соединены звездой, то в случае несимметричной трехфазной системы между нейтральными (нулевыми) точками приемника и генератора возникает напряжение смещения нейтрали

, (13)

здесь 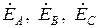– комплексы ЭДС соответствующих фаз генератора; 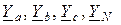– комплексные проводимости соответствующих фаз нагрузки и нейтрального (нулевого) провода.

Напряжение на фазах нагрузки

(14)

Токи в фазах

(15)

Ток нейтрального провода

. (16)

При расчете трехфазной системы «звезда – звезда с нейтральным проводом с сопротивлением » нет необходимости рассчитывать напряжение смещения нейтрали, поскольку . В этом случае трехфазную систему можно рассматривать как совокупность трех независимых контуров и рассчитывать каждый контур известными методами расчета цепей синусоидального тока. Целесообразно использовать векторные диаграммы при расчете таких цепей.

В случае отсутствия нейтрального провода в формуле (13) проводимость нейтрального провода принимают равной нулю. При этом, если генератор симметричный, а симметрия нагрузки нарушена сопротивлением нагрузки, подключенном в одной из фаз (например, ), удобно для определения напряжения смещения нейтрали воспользоваться формулой:

, (17)

для оставшихся случаев и соответственно

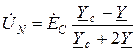; . (18)

Если нагрузка соединена звездой без нейтрального провода и известны линейные напряжения , то фазные напряжения нагрузки находятся по формулам:

. (19)

Для любой трехфазной системы сумма комплексных значений линейных напряжений равна нулю:

. (20)